Спектральное разложение стационарного процесса
Стационарным (точнее , стационарным в широком смысле) случайным процессом X(t) называется случайный процесс, математическое ожидание которого постоянно, а корреляционная функция зависит от разности своих аргументов, т.е.
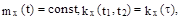 где
где 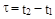 ,
, 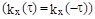
Дисперсия стационарной случайной функции постоянна
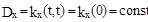
Стационарный случайный процесс X(t) называется процессом с непрерывным спектром , если существует такая действительная неотрицательная функция 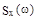 , определённая на всей оси частот
, определённая на всей оси частот 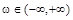 и называемая спектральной плотностью (энергетическим спектром) , что справедливы интегральные формулы Винера-Хинчина:
и называемая спектральной плотностью (энергетическим спектром) , что справедливы интегральные формулы Винера-Хинчина:
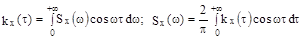
Спектральная плотность 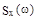 равна пределу отношения дисперсии, приходящийся на данный интервал частот ,к длине этого интервала,когда последняя стремится к нулю
равна пределу отношения дисперсии, приходящийся на данный интервал частот ,к длине этого интервала,когда последняя стремится к нулю 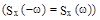
Формулы Винера - Хинчина могут быть также записаны в экспоненциальном виде
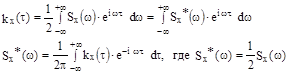
Как 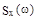 , так и
, так и 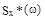 - действительные , неотрицательные чётные функции, но
- действительные , неотрицательные чётные функции, но 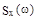 рассматривается только в интервале (0;
рассматривается только в интервале (0; 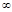 ). Дисперсия стационарного процесса с непрерывным спектром может быть выражена в виде интеграла от спектральной плотности
). Дисперсия стационарного процесса с непрерывным спектром может быть выражена в виде интеграла от спектральной плотности 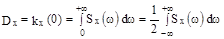
Нормированной корреляционной функций
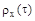 называется функция
называется функция 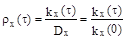
Полезными характеристиками стационарных случайных процессов с непрерывным спектром является эффективная ширина спектра
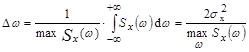 и средний интервал корреляции
и средний интервал корреляции
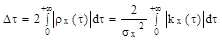
Геометрически средний интервал корреляции 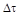 равен основанию прямоугольника с высотой
равен основанию прямоугольника с высотой 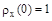 , площадь которого равна площади под кривой
, площадь которого равна площади под кривой 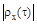 ,
, 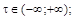 эффективная ширина спектра
эффективная ширина спектра 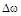 равна основанию прямоугольника с высотой
равна основанию прямоугольника с высотой 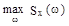 , площадь которого равна площади под кривой
, площадь которого равна площади под кривой 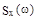 ,
, 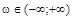
12.1 Случайная функция X(t) имеет характеристики 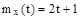 и
и 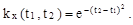
12.2 Определить стационарна ли функция 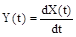 ?
?
Решение : 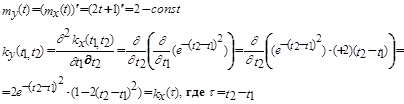
Y(t)- стационарный процесс
12.2 Случайная функция X(t) имеет характеристики
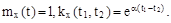
Определить являются ли стационарными функции X(t) и Y(t),
если Y(t)=t 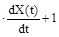 ?
?
Решение:
X(t) - стационарная функция
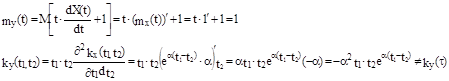
Y(t) не является стационарной функцией , т.к. 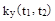
зависит не только от 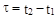 , но и от каждого из аргументов t1 и t2
, но и от каждого из аргументов t1 и t2
12.3 Случайная функция X(t) имеет характеристики
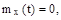
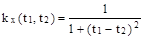 201
201
Найти характеристики случайной функции 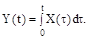
Определить стационарны ли функции X(t),Y(t) ?
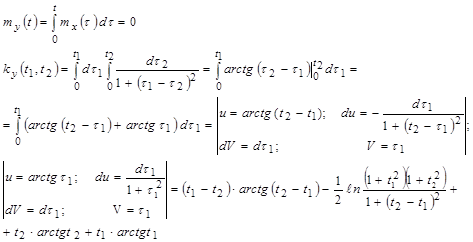 |
Решение: X(t)- стационарный процесс ,
Y(t) не является стационарным процессом , действительно,
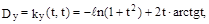 т.е. зависит от t
т.е. зависит от t
12.4 Найти характеристики случайной гармоники X(t)=A cos (ωt+ 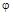 ) ,
) ,
где A и ω - неслучайные амплитуда и частота , 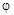 - случайная начальная фаза , равномерно распределённая на отрезке [0;2p].
- случайная начальная фаза , равномерно распределённая на отрезке [0;2p].
Показать , что X(t) -стационарный процесс
Решение :т.к. случайная величина 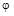 распределена равномерно на [0;2p] , то дифференциальная функция для неё f(
распределена равномерно на [0;2p] , то дифференциальная функция для неё f( 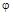 )=
)= 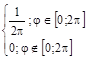
Найдём математические ожидания функций случайного аргумента 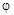 ,
,
Y=cos 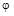 и Z=sin
и Z=sin 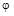
M[Y]=M[cos 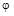 ]=
]= 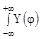 f (
f ( 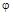 )d
)d 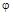 =
= 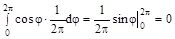
M[Z]=M[sin 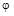 ]=
]= 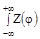 ·(
·( 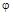 )d
)d 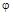 =
= 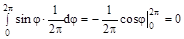
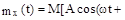
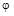 )]=
)]= 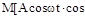
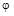 -A sin ωt sin
-A sin ωt sin 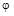 ]=
]=
=Acosωt·M[cos 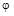 ]-Asinωt·M[sin
]-Asinωt·M[sin 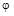 ]= 0 – 0 =0
]= 0 – 0 =0
Найдём математические ожидания функций
Y=cos2 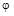 и Z=sin2
и Z=sin2 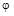
M[Y]=M[cos2 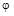 ]=
]= 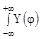 ·f(
·f( 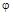 )d
)d 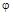 =
= 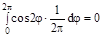
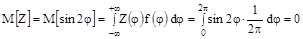

Преобразуем произведение
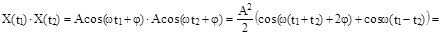
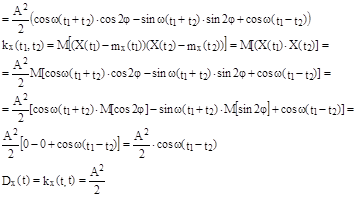
12.5 Стационарный случайный процесс X(t) имеет корреляционную функцию 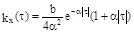 (b>0,
(b>0, 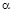 >0).
>0).
Найти корреляционную функцию и дисперсию процесса 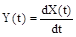 .
.
Решение :
Покажем , что
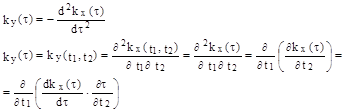
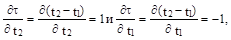
поэтому 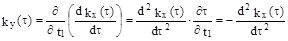
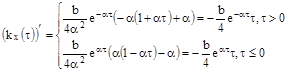 |
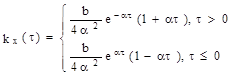
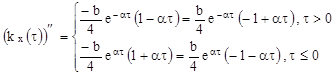 |
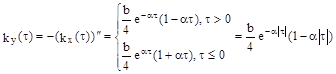
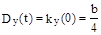
12.6 Найти корреляционную функцию шума, имеющего равномерную спектральную плотность равную 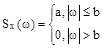
Показать что сечения процесса разнесенные на интервал 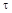 кратный величине
кратный величине 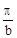 , не коррелированны
, не коррелированны
Решение :
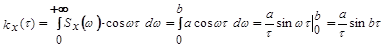
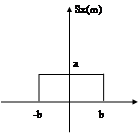
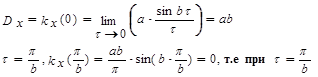
сечения не коррелированны.



12.7 Пусть X(t)- стационарный процесс со спектральной плотностью 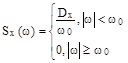 ( низкочастотный белый шум )
( низкочастотный белый шум )
Найти корреляционную функцию данного процесса
Решение:
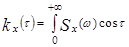 dω =
dω = 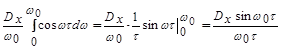
12.8 Спектральная плотность стационарного случайного процесса
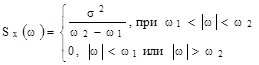
| |
при 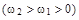 (полосовой белый шум )
(полосовой белый шум )
а) Найти корреляционную функцию 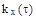 б) Рассмотреть случай
б) Рассмотреть случай 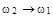 Какому случайному процессу соответствует этот предельный случай?
Какому случайному процессу соответствует этот предельный случай?
Решение:
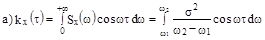
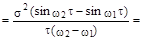

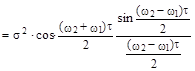



б) при 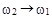

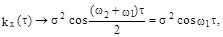
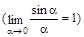 ,
,
что соответствует гармоническому колебанию на частоте 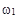
12.9 Показать , что не существует никакой стационарной случайной функции X(t), корреляционная функция которой 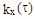 постоянна в каком-то интервале
постоянна в каком-то интервале 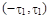 и равна нулю вне его
и равна нулю вне его
Решение :
Предположим противное , что существует случайная функция
X(t) , для которой 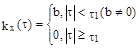 , тогда
, тогда 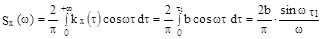
из этого выражения видно , что 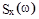 для некоторых значений отрицательна , что противоречит свойствам спектральной плотности , и, следовательно , корреляционной функции указанного выше вида существовать не может .
для некоторых значений отрицательна , что противоречит свойствам спектральной плотности , и, следовательно , корреляционной функции указанного выше вида существовать не может .
12.10 Найти средний интервал корреляции 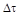 и эффективную ширину спектра
и эффективную ширину спектра 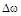 для стационарного случайного процесса с нормированной корреляционной функцией
для стационарного случайного процесса с нормированной корреляционной функцией

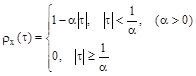
Решение :
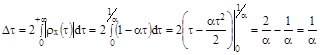
Изобразим график зависимости 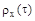
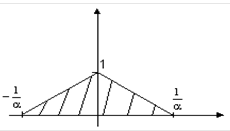
Величина 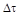 численно
численно  равна заштрихованной площади
равна заштрихованной площади
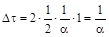
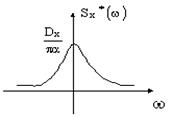
Найдём спектральную плотность случайной функции
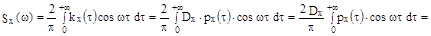
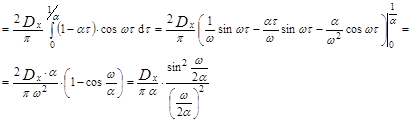
Эта функция достигает своего максимума при ω=0 , при этом
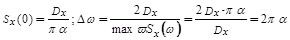
12.11. Функция X(t) - стационарный белый шум с интенсивностью 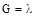 . Найти спектральную плотность X(t)
. Найти спектральную плотность X(t)
Решение: т.к. интенсивность стационарного белого шума равна 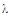 , то
, то
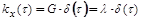 , где
, где 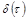 -дельта- функция.
-дельта- функция.
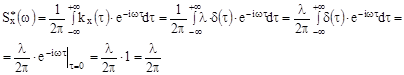
12.12. Показать что энергетический спектр случайного стационарного процесса Y(t) с корреляционной функцией 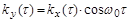 определяется при положительных частотах
определяется при положительных частотах 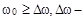 ширина спектра процесса с корреляционной функцией
ширина спектра процесса с корреляционной функцией 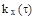 соотношением
соотношением 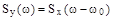 , где
, где 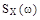 энергетический спектр стационарного процесса с корреляционной функцией
энергетический спектр стационарного процесса с корреляционной функцией 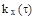
Решение :
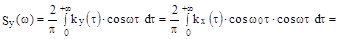
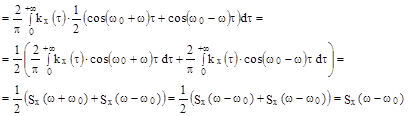
т.к. 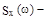 чётная функция и
чётная функция и 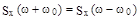
12.13. Определить спектральную плотность 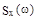 , если корреляционная функция
, если корреляционная функция 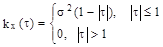
Решение: 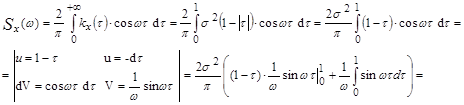
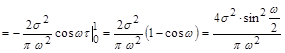
12.14 Найти спектральную плотность 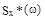 телеграфного сигнала, если
телеграфного сигнала, если 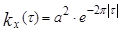
Решение:
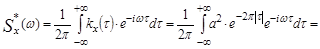
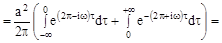
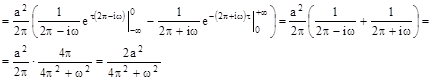
12.15 Найти энергетический спектр , эффективную ширину спектра и средний интервал корреляции стационарного марковского гауссовского шума с корреляционной функцией 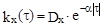
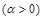
Решение : 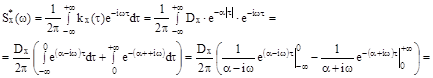
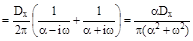
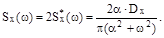
Эффективная ширина спектра 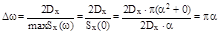
Средний интервал корреляции 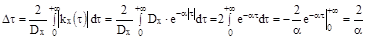
Соотношение неопределенности в данном случае 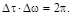
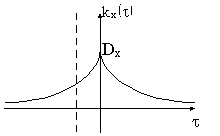 |  | ||
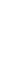 12.16. Случайная функция X(t) имеет математическое ожидание
12.16. Случайная функция X(t) имеет математическое ожидание 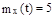 и спектральную плотность
и спектральную плотность 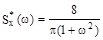 Найти корреляционную функцию случайной функции X(t)
Найти корреляционную функцию случайной функции X(t)
Решение :
В предыдущей задаче было показано , что для корреляционной функции вида 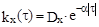 спектральная плотность имеет вид
спектральная плотность имеет вид 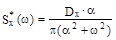
Следовательно , в нашем случае 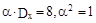
значит 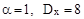 и
и 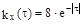
12.17 Определить корреляционную функцию , дисперсию и величину 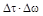 стационарного случайного процесса, имеющего спектральную плотность
стационарного случайного процесса, имеющего спектральную плотность 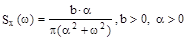
Решение :
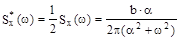 как и в предыдущей задаче
как и в предыдущей задаче
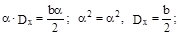
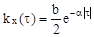
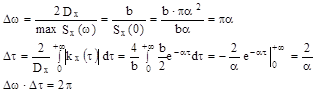
12.18. Найти спектральную плотность 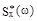 случайной функции X(t) , если её корреляционная функция
случайной функции X(t) , если её корреляционная функция 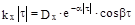
Решение:
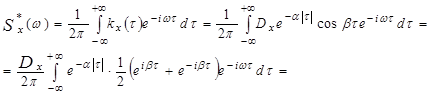
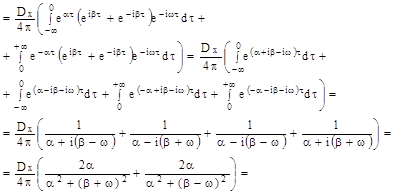
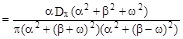









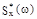
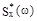
 | |||||||||||
 |  | ||||||||||
 |  | ||||||||||
 | |||||||||||




-2 2
ω = 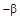 ω =
ω = 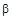 ω
ω
при 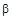 =2,
=2, 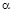 =1 при
=1 при 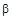 =2,
=2, 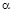 =3
=3
Вид графика 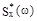 зависит от значений параметров
зависит от значений параметров 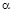 и
и 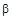
12.19. Случайная функция X(t) имеет математическое ожидание 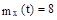 и спектральную плотность
и спектральную плотность
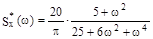
Найти корреляционную функцию случайной функции X(t)
Решение : В предыдущей задаче было показано , что для корреляционной
функции вида 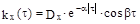 спектральная плотность имеет вид :
спектральная плотность имеет вид :
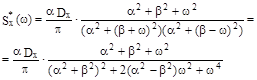
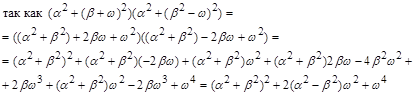
Следовательно
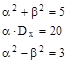
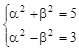
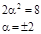
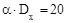 , следовательно
, следовательно 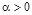 , т.е.
, т.е. 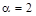
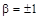 , D
, D 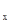 =
= 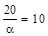
Таким образом , 
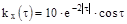
12.20. Найти спектральную плотность 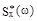 случайной функции X(t),если её корреляционная функция
случайной функции X(t),если её корреляционная функция 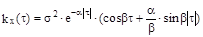
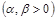
Решение: 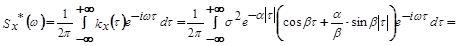
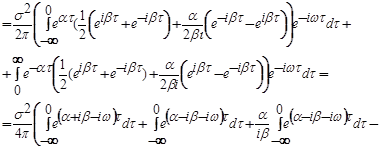
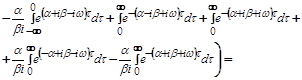
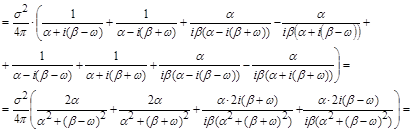
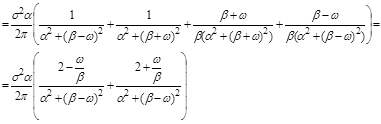
12.21. Найти спектральную плотность, эффективную ширину и средний интервал корреляции стационарного случайного процесса X(t) с корреляционной функцией 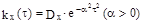
Решение :
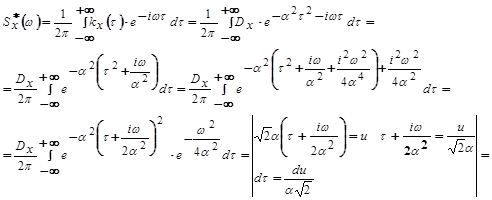
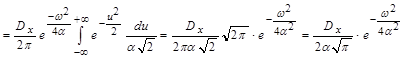
(Интеграл Пуассона 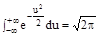 )
)
Итак , 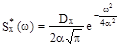 , а
, а 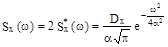
Исследуем 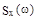 на экстремум
на экстремум
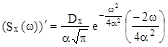 , критическая точка ω=0 знак
, критическая точка ω=0 знак 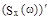

 + - ω=0 -точка max.,
+ - ω=0 -точка max.,
0 ω
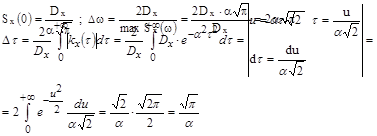 |
213
