Образ, ядро линейного оператора.

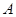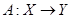Образомлинейного оператора называется множество всех векторов вида . Если , то образ 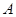есть подмножество из 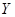. Его обозначают или .

Если 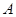- линейный оператор, то , где - какой-либо базис пространства .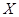

Ядро линейного оператора 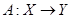- это множество тех 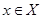, для которых . Ядро линейного оператора (обозначается ) – подпространство пространства 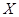. Полезно уметь находить ядра и образы линейных операторов, их размерности (дефект и ранг).

Задача 3.2.Найти образ, ядро, ранг и дефект оператора (оператор двойного векторного умножения).

Решение.Будем считать, что мы уже убедились в линейности оператора .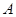

Вычисление образа. Возьмем стандартный базис пространства : . Находим

(подпространство одномерное).

.

Вычисление ядра.Пусть . Это означает, что или

Отсюда где . Другими словами , а дефект .

(В нашем примере , но это не общее правило). Можно было воспользоваться формулой для двойного векторного произведения. Но решение вряд ли упростилось бы от этого.

Как правило, нахождение ядра в конце концов сводится к решению системы линейных однородных уравнений относительно координат произвольного вектора ядра. В рассмотренном нами примере эта система оказалась очень простой

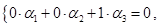
что позволило нам сразу записать общее решение .

Матрица линейного оператора в данных базисах.

Обязательно нужно научиться строить матрицу линейного оператора в данных базисах. Но кроме этого, еще раз обратим наше внимание на следующую теорему: каждый линейный оператор из 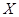в 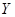однозначно определяется своими значениями на каком-либо базисе пространства 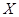. Эта теорема позволяет строить примеры различных операторов, удовлетворяющих наперед заданным свойствам.

Задача 3.3.Для каждого из нижеперечисленных условий постройте пример линейного оператора :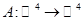

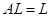1. .
2. .
3. .
4. , где .
5. На 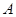действует как тождественный, но .
6. Каждое переводит в себя, но .

Решение.1. Возьмем какой-либо базис в 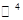, например, стандартный

.

Так как , то из условия следует . Для определенности возьмем . Определим 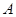на базисе так:

Этими условиями линейный оператор 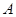полностью определен.

Если то по нашему определению

Легко убеждаемся, что .

Действительно,

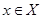- это множество тех , для которых , то есть .

6. Так как необходимо построить такой линейный оператор 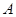, который каждое переводит в себя, но , то будем считать, что система 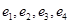является линейно независимой, а значит, является базисом 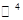. Определим 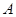на базисе так:

Можно проверить, что таким образом введенный операторм является линейным и удовлетворяет всем необходимым условиям.