Финальные вероятности состояний

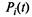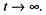Если процесс, протекающий в системе, длится достаточно дол­го, то имеет смысл говорить о предельном поведении вероятностей при В некоторых случаях существуют финальные (пре-

дельные) вероятности состояний:

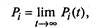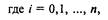не зависящие от того, в каком состоянии система 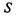находилась в начальный момент. Говорят, что в системе устанавливается пре­дельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний 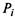уже не меня­ются. Система, для которой существуют финальные вероятности, называется эргодической, а соответствующий случайный процесс — эргодинеским.

Финальные вероятности состояний (если они существуют) мо­гут быть получены путем решения системы линейных алгебраичес­ких уравнений, которые получаются из дифференциальных уравне­ний Колмогорова, если приравнять производные к нулю, а вероят­ностные функции состояний 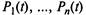в правых частях уравне­ний (2.8) заменить соответственно на неизвестные финальные вероятности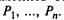

Таким образом, для системы 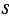с п состояниями получается си­стема 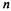линейных однородных алгебраических уравнений с п неиз­вестными 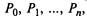которые можно найти с точностью до про­извольного множителя. Для нахождения точного значения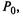 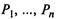к уравнениям добавляют нормировочное условие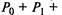

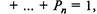пользуясь которым можно выразить любую из веро­ятностей Р, через другие и отбросить одно из уравнений.

Пример 2.3.Имеется размеченный граф состояний системы S (рис. 2.4). Необходимо составить систему дифференциальных урав­нений Колмогорова и записать начальные условия для решения этой системы, если известно, что в начальный момент система на­ходилась в состоянии S\.

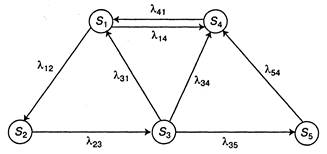
Рис. 2.4. Граф состояний системы