Матрица Грама в евклидовом пространстве

Пусть Е_n – n-мерное евклидово пространство и пусть е = (е₁, е₂,... , е_n ) – базис в нём. Так как в Е_nдля любой упорядоченной пары векторов определено их скалярное произведение, то определены скалярные произведения всех пар базисных векторов. Составим из них матрицу

Г = (41)

Матрица Гназывается матрицей Грама скалярного произведения для базиса е. Используя матрицу Грама, можно получить формулу для вычисления

скалярного произведения векторов, заданных координатами.

Пусть в базисе е заданы векторы а = х₁е₁ + х₂е₂ + … + х_nе_n , в = у₁е₁+ у₂е₂ + … + у_nе_{n .} Тогда (а, в) =(х₁е₁ + х₂е₂ + … + х_nе_n)×( у₁е₁+ у₂е₂ + … + у_nе_n) = = х ^Т×Г×у, где х ^Т– строка координат вектора а, у – столбец координатвектора в . Итак, (а, в)= х ^Т×Г×у (42).

Свойства матрицы Грама.

1⁰. Матрица Грама симметрична относительно главной диагонали.

Это следует из того, что (е_к, е_s ) = (е_s , е_к ).

2⁰. Диагональные элементы матрицы Грама строго положительны.

Это следует из того, что е_к ¹ 0 и, следовательно, (е_к, е_к ) > 0.

3⁰. Для матрицы Грама и любого n-мерногостолбца х выполняется условие х ^Т×Г×х > 0.

Это следует из 4-ой аксиомы определения скалярного произведения.

Симметрическую матрицу А, удовлетворяющую условию х ^Т×А×х > 0 для любого

ненулевого столбца х, называют положительно определённой. Следовательно, матрица

Грама положительно определённая.

4⁰. Пусть е = (е₁, е₂,... , е_n ) и е¹ = (е₁¹, е₂¹,... , е_n¹ ) –два базиса в Е_n , Ги Г¹ – матрицы Грама данного скалярного произведения в базисах е и е¹ соответственно. Пусть Т – матрица перехода от базиса е к базису е¹. Тогда (а, в)= х ^Т×Г×у, х = Т×х¹, у = Т×у¹, х ^Т= (Т×х¹)^Т= (х¹)^Т× Т^Т. Следовательно, (а, в)= ((х¹)^Т× Т^Т)× Г× (Т×у¹) = (х¹)^Т× (Т^Т× Г× Т )× у¹. Но (а, в)= (х¹)^Т× Г¹× у¹. Отсюда

Г¹ = Т^Т× Г× Т (43)

Формула (42) даёт связь матриц Грама в разных базисах.

5⁰. Определители матриц Грама во всех базисах имеют один и тот же знак.

Из формулы (42) следует ú Г¹ú =ú Т^Тú ×úГú ×úТú = úГú ×úТú ². Так как Тú ²> 0, то ú Г¹ú и ú Гú имеют одинаковые знаки.

Примеры.

1. Во множестве М₂ квадратных матриц с действительными элементами скалярное произведение задано формулой . Найти матрицу Грама этого произведения в базисе е₁ = , е₂ = , е₃ = , е₄ = .

Решение. Найдём все попарные произведения базисных элементов: (е₁, е₁) = 1, (е₁, е₂) = (е₂, е₁) = 0, (е₁, е₃) = (е₃, е₁) = 0, (е₁, е₄) = (е₄, е₁) = 0, (е₂, е₂) = 1, (е₂, е₃) = (е₃, е₂) = 0, (е₂, е₄) = (е₄, е₂) = 0, (е₃, е₃) = 1, (е₃, е₄) = (е₄, е₃) = 0, (е₄, е₄) = 1. Следовательно,

Г = .

2. В пространстве R[х] многочленов степени не выше 3-х скалярное произведение задано формулой , где a и b – фиксированные действительные числа, a < b. Составить матрицу Грама в базисе (1, х, х², х³).

Решение. Найдём все попарные произведения базисных элементов: (1, 1) = = b – a,

(1, х) = (х, 1) = = ), (1, х²) = (х², 1) = = ), (1, х³) = (х³, 1) = = ), (х, х) = = ), (х, х²) = (х², х) = = ), (х, х³) = (х³, х) = = ), (х², х²) = = ), (х², х³) = (х³, х²) = = ), (х³, х³) = = ). Матрица Грама будет иметь вид:

Г = .

3. В базисе (е₁, е₂, е₃) пространства Е₃ скалярное произведение задано матрицей Грама Г = . Найти скалярное произведение векторов а = (1, –5, 4) и в = (–3, 2, 7).

Решение. Используя формулу (41), получим (а, в) = (1, –5, 4) × × = 7.

Введение метрики в евклидовом пространстве

Пусть Е_n – n-мерное евклидово пространство. Скалярное произведение вектора самого на себя назовём скалярным квадратом этого вектора, т.е. (а, а) = а². По 4-ой аксиоме скалярного произведения а² ³ 0.

Определение 47. Длиной вектора называется арифметическое значение квадратного корня из скалярного квадрата этого вектора . т.е. ú аú = 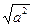(44)

Свойства длины вектора:

1. Любой вектор а имеет длину и только одну, ú аú ³ 0.

2. ú a×аú = úaú×ú аú для любого а Î Е_n .

3. Для любых векторов а и в из Е_n верно неравенство ú а×вú £ú аú ×ú вú.

Доказательство. (а –aв)² = а² – 2a(а, в) + a²×в² ³ 0 для любого a Î R. Так как квадратный трёхчлен неотрицателен при любом значении a, то его дискриминант неположителен, т.е. (а, в)² – а²× в² £ 0, или (а, в)² £ а²× в². Отсюда ú а×вú £ú аú ×ú вú (45). Знак равенства в этой формуле будет тогда и только тогда, когда векторы пропорциональны.

Определение 48.Вектор единичной длины называется единичным вектором или ортом.

4⁰. Для любого ненулевого вектора существует пропорциональный с ним орт.

Если а ¹ 0, то ú аú ¹ 0. Следовательно, существует вектор а₀ = а. Очевидно, ú а₀ú =1.

Определение 49. Углом между ненулевыми векторами аи 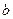называется такое действительное число j , что (46).

Угол между векторами а и 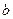можно также обозначать .

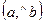Свойства углов.

1⁰.Для любых двух ненулевых векторов угол между ними определён.

Из формулы (44) следует, что Следовательно, j существует.

2⁰. Если a ¹ 0, b ¹ 0, то .

Определение 48. Два ненулевых вектора называются ортогональными, если их скалярное произведение равно нулю.

Ортогональные векторы обозначаются а ^ в.

3⁰. Если а ^ в, a ¹ 0, b ¹ 0, то (aа)^ (bв).

4⁰. Если а ^ в и а ^ с, то а ^ (в + с).

Определение 50. Множество всех векторов пространства Е_n, ортогональных вектору а, к которому добавлен нулевой вектор, называется ортогональным дополнением вектора а.

5⁰. Ортогональное дополнение к вектору а является (n – 1)-мерным евклидовым подпространством в Е_n .

Доказательство.

Из свойств 3⁰ и 4⁰ следует, что рассматриваемое множество L является линейным подпространством в Е_n . Так как в Е_n определено скалярное произведение, то оно определено и в ортогональном дополнении, следовательно, L является евклидовым подпространством. Кроме того, с Î L Û (а, с) = 0 (*). Зафиксируем в Е_n базис. Пусть а = (а₁, а₂, … , а_n), с = (х₁, х₂, … , х_n). Тогда с Î L Û а ^Т×Г×х = 0 (**). Уравнение (**) есть линейное однородное уравнение с n неизвестными. Фундаментальная система его решений состоит из (n – 1) решения. Следовательно, пространство решений уравнения (**) является (n – 1)-мерным.

Пусть Е_к – подпространство пространства Е_n. Обозначим Е множество, состоящее из нулевого вектора и всех векторов, ортогональных любому ненулевому вектору из Е_к .Иными словами с Î Е Û (с, а) = 0 для всех а Î Е_к . Пространство Е ортогональным дополнением к пространству Е_к .

6⁰.Ортогональное дополнениеЕ является (n – к)-мерным евклидовым подпространством в пространстве Е_n .

Доказательство аналогично доказательству свойства 5⁰.

7⁰.Е Ç Е_к = {0}.

8⁰. Любые два ортогональных вектора линейно независимы.

Доказательство. Пустьа ^ в. По определению эти векторы ненулевые. Предположим, что они линейно зависимы, т.е. существует такая ненулевая пара a, b действительных чисел, что a×а + b×в = 0. Если a ¹ 0, то умножим обе части последнего равенства скалярно на вектор а.Получим a×а²+b×(а, в) = 0. Так как (а, в) = 0 и а²¹ 0, то a = 0. Противоречие. Следовательно, а и влинейно независимы.

9⁰. Если а₁, а₂, … , а_к и в₁, в₂, … , в_s – две системы линейно независимых векторов и каждый вектор первой системы ортогонален любому вектору второй, то система векторов а₁, а₂, … , а_к и в₁, в₂, … , в_s линейно независима.

Теорема 42. Для любого к (1 £ к £ n ) Е_n = Е Å Е_к .

Доказательство. Пусть (е₁, е₂,... , е_к ) – базис в Е_к и (е_{к +1}, е _{к + 2},... , е_n ) – базис в Е . Из свойства 9⁰ следует, что (е₁, е₂,... , е_к, е_{к +1}, е _{к + 2},... , е_n ) будет линейно независимой. Так как в ней n векторов,то это базис в Е_n . Следовательно, Е_n = Е + Е_к .Из свойства 7⁰ следует Е_n = Е Å Е_к .

Пусть Е_n = Е Å Е_к . Если а – любой вектор из Е_n , то а = а₁ + а₂, где а₁ Î Е_к , а₂ Î Е . Вектор а₁ называется проекцией вектора а на подпространство Е_к .Вектор а₂ называется ортогональной составляющей вектора а.