Потенциалы электромагнитного поля

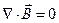(1)

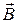-соленоидальный. Его всегда можно положить равным ротору некоторый вспомогательный вектор .

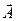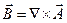(2)

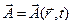- вспомогательный вектор, называемый вектор-потенциалом.

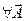
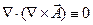
Подставим (2) в первое уравнение Максвелла:

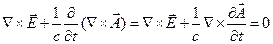
Откуда .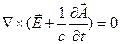

Таким образом , 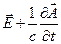является потенциальным и его можно представить в виде:

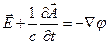(3)

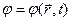- некоторая скалярная функция координат и времени, названная скалярным потенциалом.

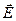нельзя представить в виде градиента от некоторой скалярной функции.

Он имеет вихревой характер:

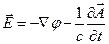(4)

причём 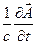выражает закон электромагнитной индукции.

Если скалярный и векторный потенциалы введены, то уравнение первой группы Максвелла удовлетворяются тождественно. 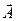и определяются из уравнений второй группы Максвелла.

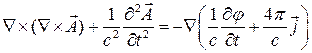
Учитывая, что 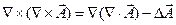, где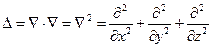

получаем: 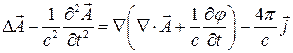(5)

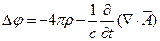(6)

Потенциалы А и – вспомогательные величины, введённые для упрощения, они не изменяют 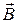и 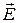, но позволяют сделать (5) и (6) независимыми. Для однозначного знания поля 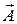необходимо знать его ротор и дивергенцию. Но векторный потенциал А введён посредством (2), т.е. задан лишь ротор 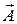, а дивергенция – нет. Зададим её значение:

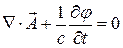(7) – соотношение Лоренца.

Тогда (5) – (6) примут вид:

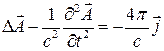(8)

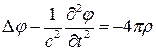(9)

Т.е. переменные разделились.

(8) – (9) эквивалентны исходным уравнениям Максвелла.

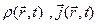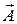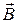Если заданы , удовлетворяют уравнениям непрерывности, то интегрирование (8),(9) даст и ,а и 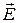получим из (2),(4).

Уравнения типа 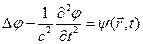, где 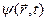- заданная функция координат и времени называют уравнениями Даламбера.

Вводя оператор Даламбера

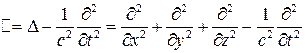
это уравнение записывают в компактной форме:

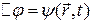(10)

Если 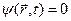,то (10) переходим в волновое уравнение:

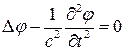(11)

Если 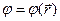, , 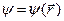(т.е. эти функции не зависят от времени), уравнение Пуассона:

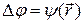(12)

С математической точки зрения, уравнения (10) – (12) проще уравнений Максвелла (в интегральной форме). Поэтому метод потенциалов представляет основной расчётный аппарат теории поля.

Калибровочная инвариантность потенциалов.

Определение потенциалов 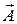и является неоднозначным и допускает известный произвол. Обсудим вопрос о степени этого произвола. Из определения вектора-потенциала следовательно что если совершить преобразование:

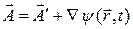(1) где 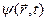- произвольная функция, то мы придём к тому же значению .

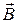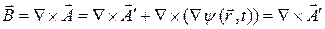
Таким образом, 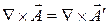. При этом для 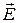получаем:

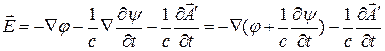
Производя замену 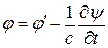(2), получим прежнее выражение для 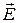, но уже через 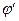и .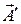

Таким образом, вектор-потенциал определён с точностью до градиента произвольной функции 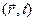,а скалярный потенциал до произвольной по t той же функции. В общем случае, два поля, описываемые потенциалами 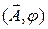, 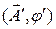физически тождественны, есл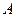и 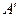и , и 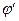могут быть связаны соотношениями (1)-(2). Иначе говоря , уравнения электродинамики неизменны, инвариантны по отношению к (1),(2).

Различные способы выбора 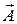и , оставляющие неизменным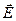и и 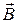, называются различными калибровками потенциалов. Инвариантность 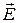и 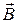по отношению к калибровкам называют калибровочной/градиентной инвариантностью. (1) – (2) – калибровочные преобразованиями. Свойства калибровочной инвариантности подбирать потенциалы так, чтобы соотношения теории поля приняли максимально простой вид.

Например, соотношение Лоренца, отвечающие калибровке Лоренца. Убедимся, что такая калибровка всегда возможна.

Пусть для 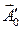, 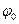соотношение Лоренца не выполняется:

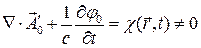
Произведём калибровочные преобразования: ,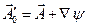

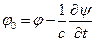
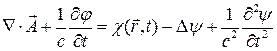(3)

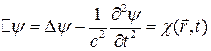(4)

Условия Лоренца будут выполняется. Так как (4) будет выполнятся для любого , то калибровка Лоренца всегда возможна.

Произвольная функция 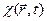не определяется полностью уравнением (4). К ней можно добавить произвольную 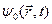, такаю .

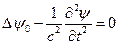Совершая преобразование: ,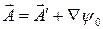

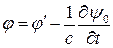
Приходим к тем же значением 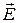и .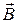

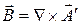
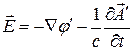
При этом 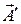и 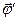удовлетворяет условию Лоренца:

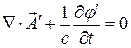
Поэтому можно подобрать 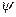так, чтобы выполнялось ещё одно условие, налагаемое на .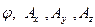