Уравнения Максвелла для электромагнитного поля в среде с учетом пространственно-временной дисперсии

При рассмотрении сред с пространственно-временной дисперсией мы учитываем зависимость диэлектрической проницаемости как от час­тоты, так и от волнового вектора.

В случае линейной изотропной среды с пространственно- временной дисперсией зависимость вектора индукции электрического поля от вектора напряженности имеет вид:

(22)

или

здесь под понимаем тензор. Далее везде, где учитывается

пространственная дисперсия (даже в изотропном случае), диэлектриче­ская проницаемость является тензором.

Пространственная дисперсия возникает потому, что индукция D в какой-либо точке r определяется электромагнитным полем (Е ; В ) не только в той точке, но и в некоторой ее окрестности.

Временная дисперсия возникает вследствие того, что D в момент времени t определяется только полем в прошлом и настоящем (прин­цип причинности) [8, с. 202].

Если свойства среды стационарны и пространственно однородны, то ядро оператора £ будет зависеть только от разностей:

Тогда (22) можно переписать в виде

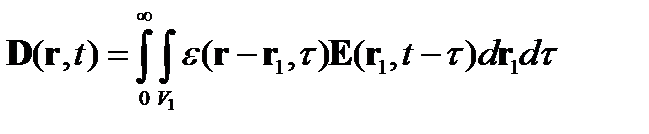
Запишем поля Е и D в виде фурье-компонент. Для этого выпол­ним следующие преобразования:

Таким образом, приходим к уравнению связи:

В случае пространственно-временной дисперсии уравнения Максвелла принимают вид:

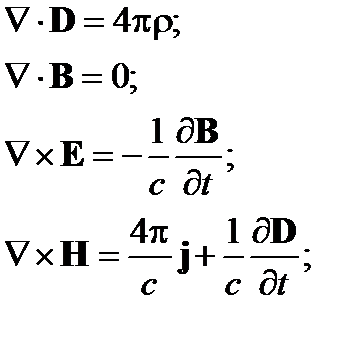
получаются усреднением точных микроскопических уравнений поля в вакууме. Однако в этом случае

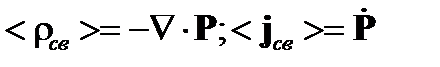
Здесь мы полагаем 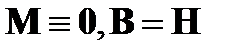, так как Р не связано с Е локаль­ным образом, как это было в отсутствие пространственной дисперсии [1, § 103]. Например,

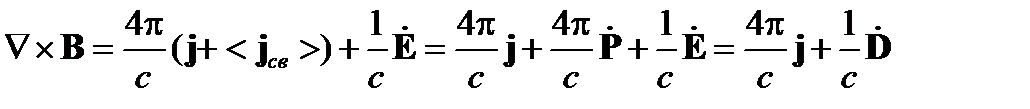
Плоские монохроматические волны:

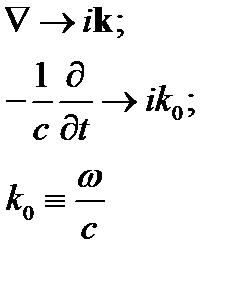
В отсутствие пространственной дисперсии Далее рассмотрим случай однородной среды:

Без пространственной дисперсии	С пространственной дисперсией
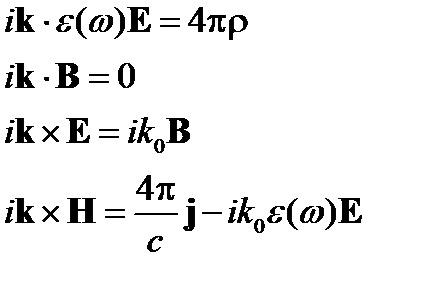