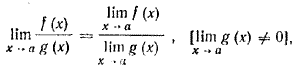Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида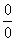

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Пример 6

Найти предел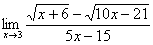

Начинаем решать.

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

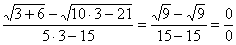
Получена неопределенность вида , которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов:
И смотрим на наш предел: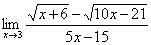
Что можно сказать? 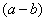у нас в числителе уже есть. Теперь для применения формулы осталось организовать 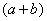(которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

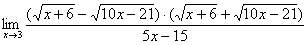
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

Хорошо, 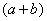мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

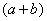То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :

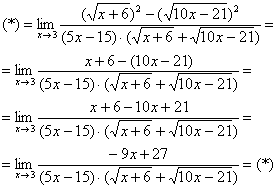
Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.

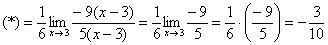
Готово.

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Пример 7

Найти предел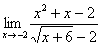

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

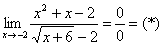
Разложим числитель на множители:

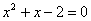
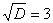
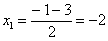
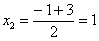
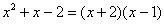
Умножим числитель и знаменатель на сопряженное выражение

Приведем без доказательства основные теоремы о пределах функций. Эти теоремы вполне аналогичны тем, которые мы рассматривали (также без доказательства) ранее при изучении пределов числовых последовательностей.

1. Предел константы равен самой этой константе:

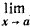с = с.

2. Постоянный множитель можно выносить за знак предела:

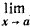[ k • f (х)] = k • 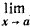f (х).

3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:

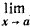[ f (х) ± g (х)] = 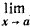f (х) ± 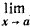g (x).

4. Предел произведения функций равен произведению пределов этих функций:

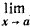[ f (х) • g (х)] = 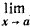f (х) • 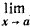g (x).

5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю: