Способы задания бинарных отношений.

Виды бинарных отношений на множестве A

1) Обратное отношение .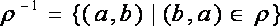

2) Дополнение .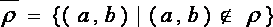

3) Тождественные .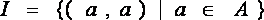

4) Универсальные .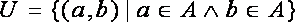

Композиция отношений

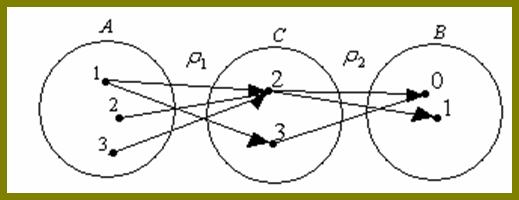
Пусть P1 - отношение из A в C , 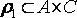И P2 - отношение из C в В,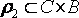

тогда композицией отношений называется отношение

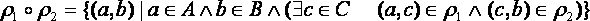
ПРИМЕР

, , .

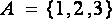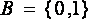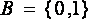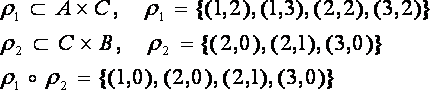
Пусть 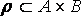( 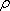отношение из А в В). Ядром отношения называется композиция отношения и обратного для него отношения 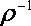, т.е. .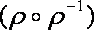

Основные законы теории множеств

1. Коммутативность операций ∪ и ∩:

а) A∪B=B∪A б) A∩B=B∩A

2. Ассоциативность операций ∪ и ∩:

а) A∪(B∪C)=(A∪B) ∪C б) A∩(B∩C)=(A∩B) ∩C

3. Законы идемпотентности операций ∪ и ∩:

а) A∪A=A б) A∩A=A

4. Законы дистрибутивности:

а) A∪(B∩C)=(A∪B) ∩ (A∪С) б) A∩(B∪C)=(A∩B) ∪ (A∩С)

5. Законы поглощения:

а) A∪(A∩B)=A б) A∩(A∪B)=A

6. Законы де Моргана:

а) A∪ B = A∩ B б) A∩ B = A∪ B

7. Законы пустого и универсального множеств: ∅=Æ

A∪∅= A A∩∅= ∅ A∩ A=∅

A∪U=UA∩U= A A∪ A=U

U=∅ ∅ = U

8. Закон двойного отрицания:

A = A

Пример 4. [ , ] Доказать, что относительно данного универсальног

множества U дополнение A любого множества A, если A⊂ U, единственно.

4Для доказательства единственности дополнения A множества A⊂ U

предположим, что существует два множества B и C, каждое из которы

удовлетворяет требованиям дополнения множества A, т.е. их пересечение с A

пусто, а объединение с A дает U:

а) B ∩ A =∅; б) C ∩ A =∅; в) B ∪ A =U ; г) C ∪ A =U .

Очевидно, что B = B ∩U . С учетом условия г) B = B ∩(C ∪ A). Так ка

B ∩(C ∪ A) = (B ∩C)∪(B ∩ A), то с учетом условия а) B = (B ∩C) ∪∅ = B ∩C .

Аналогично исходя из условий в), б) получим:

C = C ∩U = C ∩(B ∪ A) = (C ∩ B)∪(C ∩ A) = (C ∩ B)∪∅ = C ∩ B .

Итак, мы получили, что B = B ∩C и C = C ∩ B . Так как C ∩ B = B ∩C

(коммутативность операции пересечения), то B = C, что и требовалось доказать.3

БИНАРНЫЕ ОТНОШЕНИЯ

2.1.Основные определения

Бинарные отношения используются для определения каких-либ

взаимосвязей, которыми характеризуются пары элементов множества, т.е. есл

отношение P определено на множестве A×B (P⊂A×B), то это значит, что

множество P попадут только те пары множества A×B, между элементами которы

имеет место указанное отношение.

Способы задания бинарных отношений.

Так как отношения – это множества, то их можно задавать перечислением ил

характеристическим свойством. Кроме того, для бинарных отношений

определенных на конечных множествах, есть еще несколько способов их задания.

1. Бинарное отношение P⊂A×B, где A={a1, a2, …, an}, B={b1, b2, …, bm} може

быть задано (m,n)-матрицей (таблицей) (m строк, n столбцов), в которой элемен

ij p , стоящей на пересечении i-й строки и j-го столбца, равен 1, если межд

элементами ai и bj имеет место отношение P, или 0 в противном случае.

Например, отношение P={(a,b) | a∈A, b∈B и a>b}, где A={6,7,8}, B={5,6,7,8,9

задано характеристическим свойством. Это же отношение

может быть определено перечислением P={(6,5), (7,5),

(7,6), (8,5), (8,6), (8,7)} или матрицей отношения.

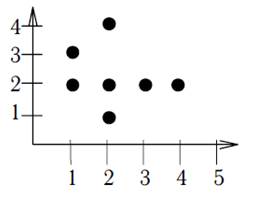
2. Если P⊂A×B, A и B – числовые множества,

то отношение P можно изобразить как

множество точек на плоскости, где каждая

точка представляет собой пару из множества P.

Например, P={(2,1), (1,2), (2,2), (3,2), (4,2), (1,3),

(2,4)}, где A={1,2,3,4,5}, B={1,2,3,4}

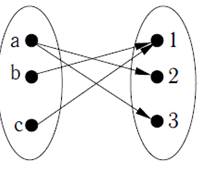
3. Если P⊂A×B, то отношение P можно

изобразить в виде диаграммы, состоящей из

узлов и стрелок, при этом узлам взаимно

однозначно соответствуют элементы множеств A

и B, а стрелка соединяет элемент a и с элементом

b только в том случае, если (a, b)∈P. Например,

P={( a,2), (a,3), (b,1), (c,1)}, A={a, b, c}, B={1, 2,

3}

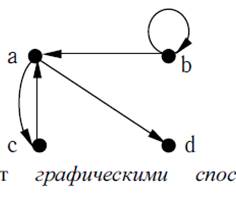
4. Если P⊂A2, то бинарное отношение может

быть задано в виде графа, вершины которого –

элементы множества, а дуги направленные от a к

b означают, что (a, b)∈P. Например, P={( a, c), (c,

a), (b, a), (b, b) ,(a, d)}, где A={a, b, c, d}.

Способы задания 2–4 иногда называют графическими способам

отображения бинарных отношений.

Пусть P – некоторое бинарное отношение.

Областью определения P называется множество

äP={x|(x,y)∈Ñ для некоторого y}.

Областью значений P называется множество

ñP={y|(x,y)∈Ñ для некоторого x}.

Так как бинарное отношение по сущности есть множество, то для нег

определены все операции, которые определены для множеств: пересечение

объединение, разность, симметрическая разность и дополнение. При этом вс

законы алгебры множеств сохраняют свою силу. Кроме того, определяются други

операции над отношениями, в том числе:

Обратным к P отношением называется множество

P–1={(y,x)|(x,y)∈Ñ }.

Композицией бинарных отношений P1⊂A×B и P2⊂B×C называется множеств

P3= 1 2 P _ P , где P3⊂A ×C и P3={(x,y) | x∈A, y∈C и найдется z∈B такой, что (x,z)∈P1

(z,y)∈P2}.

Образом множества X относительно P называется множество

P(X)={y|(x,y)∈Ñ для некоторого x∈X}.

Множество P−1(Y)={x|(x,y)∈Ñ для некоторого y∈Y} называется прообразом

множества Y относительно P.