Признаки существования пределов
Не всякая функция, даже ограниченная, имеет предел. Например, функция 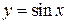 при
при 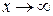 предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования пределов.
предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования пределов.
Теорема 5. (О пределе промежуточной функции)
Если функция 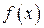 заключена между двумя функциями
заключена между двумя функциями 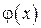 и
и 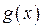 , стремящимися к одному и тому же пределу, то она также стремиться к этому пределу, т.е. если
, стремящимися к одному и тому же пределу, то она также стремиться к этому пределу, т.е. если 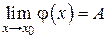 ,
, 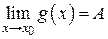 и
и 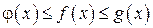 , то
, то
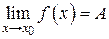 .
.
Доказательство:
Так как 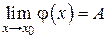 и
и 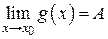 , то для любого
, то для любого 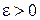 существуют две окрестности
существуют две окрестности 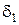 и
и 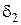 точки
точки 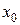 , для всех точек которых соответственно выполняются неравенства
, для всех точек которых соответственно выполняются неравенства
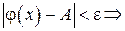
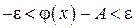 и
и 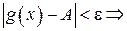
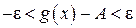 .
.
Пусть 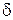 – меньшее из чисел
– меньшее из чисел 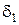 и
и 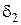 . Тогда в
. Тогда в 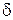 – окрестности точки
– окрестности точки 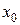 выполняются оба неравенства.
выполняются оба неравенства.
По условию 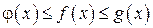 , тогда
, тогда 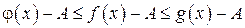 .
.
Получаем 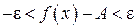 или
или 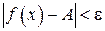 . Это значит, что
. Это значит, что 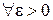
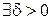
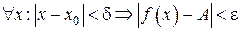 , т.е.
, т.е. 
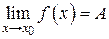 . Ч. и т. д.
. Ч. и т. д.
Теорема 6. (О пределе монотонной функции)
Если функция 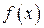 монотонна и ограничена при
монотонна и ограничена при 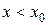 или при
или при 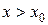 , то существует соответственно её левый предел
, то существует соответственно её левый предел 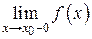 или её правый предел
или её правый предел 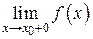 .
.
Теорема 7. (Вейерштрасса)
Ограниченная монотонная последовательность 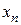 ,
, 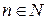 , имеет предел.
, имеет предел.
Заметим, что теорему 7 можно считать следствием теоремы 6.
Замечательные пределы
Первым замечательным пределом называется предел вида
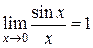 (2.2.1)
(2.2.1)
Доказательство:
Для доказательства формулы (2.2.1) рассмотрим круг радиуса 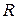 с центром в точке
с центром в точке 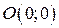 .
.
 Пусть
Пусть 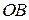 – радиус вектор точки
– радиус вектор точки 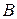 , лежащей на окружности радиуса
, лежащей на окружности радиуса 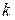 с центром в точке
с центром в точке 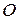 , образующий угол
, образующий угол 
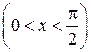 с осью
с осью 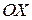 , дуга
, дуга 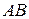 численно равна центральному углу
численно равна центральному углу  (см. рис. 2.2.2).
(см. рис. 2.2.2).
На рис.2.2.2 видно, что площадь треугольника 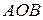 меньше площади сектора
меньше площади сектора 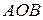 , которая в свою очередь меньше площади прямоугольного треугольника
, которая в свою очередь меньше площади прямоугольного треугольника 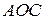 , т. е.
, т. е.
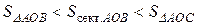 .
.
Так как 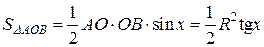 , то имеем
, то имеем
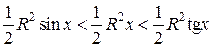 .
.
Разделим все части полученного двойного неравенства на 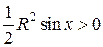 , получаем
, получаем 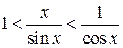 или
или 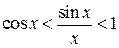 .
.
Так как функции 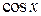 и
и 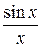 четные, то полученные неравенства справедливы и при
четные, то полученные неравенства справедливы и при 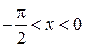 .
. 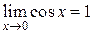 и
и 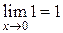 .
.
Тогда по признаку (о пределе промежуточной функции) существования предела (см. теорему 5 п. 2.2.3) 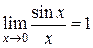 . Ч. и т. д.
. Ч. и т. д.
Примеры.
1. 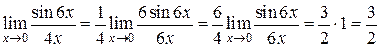
2. 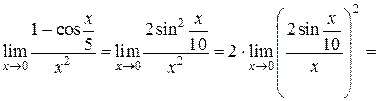
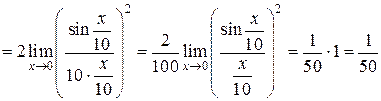 .
.
Вторым замечательным пределом называется предел вида
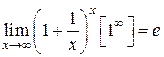 (2.2.2)
(2.2.2)
или
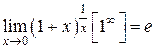 . (2.2.3)
. (2.2.3)
Доказательство:
Для доказательства формулы (2.2.2) рассмотрим прежде предел числовой последовательности 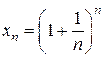 ,
, 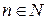 при
при 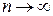 .
.
Докажем, что эта последовательность удовлетворяет теореме Вейерштрасса (см. теорема 7 п. 2.2.3), т.е. имеет предел и он равен 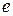 , иначе говоря
, иначе говоря
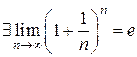 . (2.2.4)
. (2.2.4)
Докажем, что последовательность 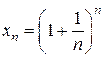 возрастающая, а значит монотонная, и что она ограничена.
возрастающая, а значит монотонная, и что она ограничена.
По формуле бинома Ньютона
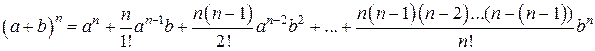 .
.
Полагая 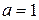 ,
, 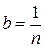 , получим
, получим
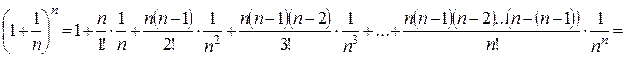
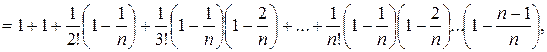
т. е.
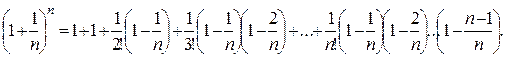 (2.2.5)
(2.2.5)
Из последнего равенства следует, что с увеличением 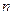 число положительных слагаемых увеличивается, число
число положительных слагаемых увеличивается, число 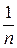 убывает, поэтому величины
убывает, поэтому величины 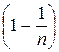 ,
, 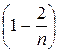 ,
, 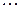 возрастают, поэтому последовательность
возрастают, поэтому последовательность 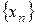 – возрастающая, при этом
– возрастающая, при этом
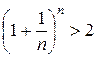 . (2.2.6)
. (2.2.6)
Покажем, что последовательность 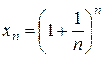 – ограничена. Заменим каждую скобку в правой части равенства (2.2.5) на единицу; правая часть увеличится, получим неравенство
– ограничена. Заменим каждую скобку в правой части равенства (2.2.5) на единицу; правая часть увеличится, получим неравенство
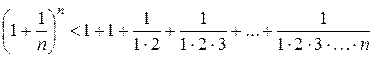 .
.
Усилим полученное неравенство, заменив числа 3, 4, 5, …, стоящие в знаменателях дробей, числом 2:
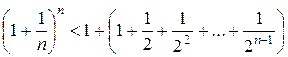 .
.
Сумму в скобке найдем по формуле суммы 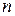 членов бесконечно убывающей геометрической прогрессии с
членов бесконечно убывающей геометрической прогрессии с 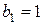 и
и 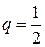 :
:
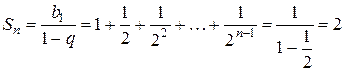 .
.
Поэтому
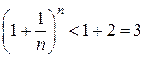 . (2.2.7)
. (2.2.7)
Итак, последовательность 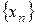 – ограничена, при этом для
– ограничена, при этом для 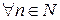 выполняются неравенства (2.2.6) и (2.2.7):
выполняются неравенства (2.2.6) и (2.2.7):
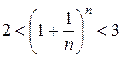 .
.
Следовательно, на основании теоремы Вейерштрасса последовательность 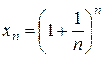 ,
, 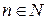 , имеет предел, обозначенный
, имеет предел, обозначенный 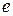 :
: 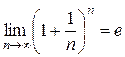 . Ч. и т. д.
. Ч. и т. д.
Число 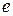 называется неперовым числом. Число
называется неперовым числом. Число 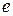 иррациональное, его приближенное значение равно
иррациональное, его приближенное значение равно 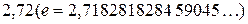 . Число
. Число 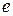 принято за основание натурального логарифма.
принято за основание натурального логарифма.
Докажем теперь что к числу 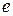 стремится и функция
стремится и функция 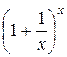 при
при 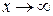
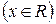 :
: 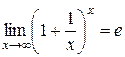 .
.
1. Пусть 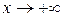 .
.
Каждое значение  заключено между двумя положительными целыми числами:
заключено между двумя положительными целыми числами: 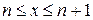 , где
, где 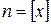 – это целая часть числа
– это целая часть числа  . Отсюда следует
. Отсюда следует 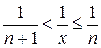 ,
, 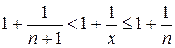 , поэтому
, поэтому
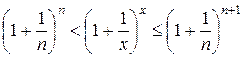 .
.
Если 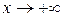 , то
, то 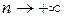 . Поэтому согласно формуле (2.2.4), имеем:
. Поэтому согласно формуле (2.2.4), имеем:
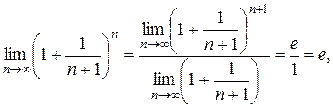
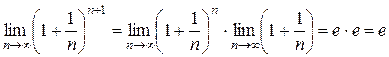 .
.
По признаку (о пределе промежуточной функции) существования пределов (см. теорему 5 п. 2.2.3)
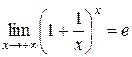 (2.2.8)
(2.2.8)
2. Пусть 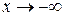 .
.
Сделаем подстановку 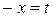 , тогда
, тогда 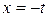 и при
и при 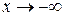 ,
, 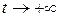 . Получаем
. Получаем 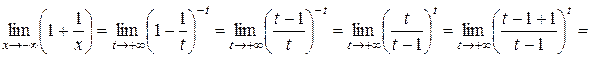
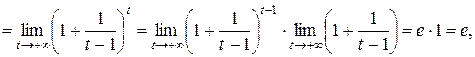 т. е.
т. е.
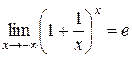 (2.2.9)
(2.2.9)
Из равенств (2.2.8) и (2.2.9) вытекает равенство (2.2.2), т.е.
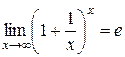 . Ч. и т. д.
. Ч. и т. д.
Докажем равенство (2.2.3) 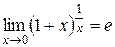 : выполним подстановку
: выполним подстановку 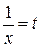 , тогда
, тогда 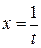 и при
и при 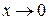 ,
, 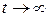 . Получаем
. Получаем 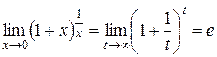 . Ч.и т. д.
. Ч.и т. д.
Примеры.
1. 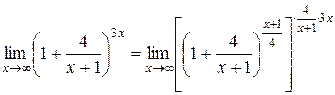 , т.к.
, т.к. 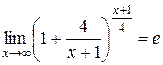 ,
, 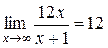 , то окончательно получим
, то окончательно получим 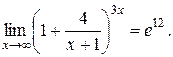
2. 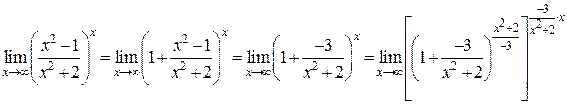 ,
,
т.к. 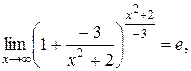
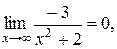
то окончательно получим 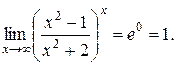
3. 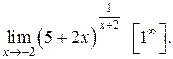
Выполним подстановку 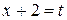 , тогда
, тогда 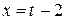 и при
и при 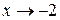 ,
, 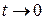 .
.
Получаем
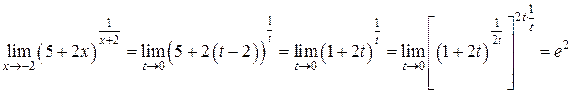 .
.
Используя прием, рассмотренный в приведенных выше примерах можно найти множество других пределов.
При вычислении пределов вида 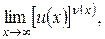 где
где 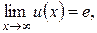 возможны варианты.
возможны варианты.
1. Если 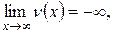 то
то 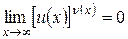 .
.
2. Если 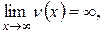 то
то 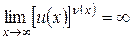 .
.
