Уравнение состояния идеального газа

Опыт показывает, что в состоянии термодинамического равновесия термодинамические параметры объём V, давление P и температура T не являются независимыми. Каждая из них является функцией двух других. Уравнение, связывающее все три величины – давление, объём и температуру вещества, для данной его массы называется уравнением состояния и может быть записано в виде

j(V,T,P)=0 (1.1)

Уравнение состояния принадлежит к числу важнейших характеристик макроскопических свойств однородных тел. Уравнение состояния нельзя ввести теоретически из общих принципов термодинамики, его можно получить, используя аппарат статистической физики или же результаты экспериментов. Если известно уравнение состояния, то с помощью аппарата термодинамики можно определить все интересующие свойства вещества. К сожалению, известно точное уравнение состояния только для так называемого идеального газа, которое определятся уравнением Менделеева - Клайперона и имеет следующий вид:

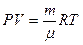, (1.2)

где R- универсальная газовая постоянная, причём R=8,314 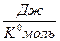. Для термодинамического описания реальных систем применяются эмпирические уравнения состояния с двумя и более подгоночными параметрами.

Уравнение состояния (1.2), записанное для данной массы m идеального газа, можно переписать для случая количества частиц N. Для этого в формулу (1.2) вместо массы газа, поставим её значение m=m_oN, где m_o – масса одной частицы, молярную массу m заменим на m=m_oN_A, тогда получим:

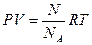(1.3)

Воспользуясь тем, что R/N_A=k_Б, где k_Б коэффициент Больцмана

(k_Б =1.38×10^-23Дж/К), имеем

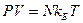(1.4)

Законы идеальных газов

Процессы, происходящие в системах при постоянном значении одного из трёх параметров P,V,T называются изопроцессами.

Изотермический процесс

Процессы, происходящие при постоянной температуре, называются изотермическими. Если в уравнении (1.2) положить T=const, то видно, что вся правая часть уравнения оказываемся постоянной величиной, т.е.

PV=const (1.5)

Это формула, которая называется уравнением изотермы, представляет собой закон Бойля – Мариотта. Согласно этому закону при постоянной температуре изменение давления и объёма происходят так, что произведение давления на объём остаётся величиной постоянной. Уравнение (1.5) выполняется, если масса газа при этом процессе остаётся постоянной.

Свойство любого тела изменять свой объём при изменении давления называется сжимаемостью. Если изменение объёма происходит, так что температура остаётся постоянной, то сжимаемость характеризуется изотермическим коэффициентом сжимаемости c, который определяется следующим образом

c 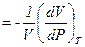. (1.6)

Знак минус связан, тем, что 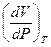<0, а коэффициент принято считать положительным.

Изобарический процесс

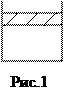Пусть теперь газ находиться в условиях, когда постоянным сохраняется его давление. Такие условия можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем (рис.1). В таком цилиндре всякое изменение давления вызывает движение поршня и изменение объёма газа, так что давление остаётся постоянным. Перепишем уравнение (1.2) следующим образом:

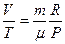. (1.7)

При постоянном давлении и массе газа правая часть уравнения (1.7) является постоянной величиной, т.е.

.

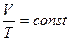Это уравнение называется уравнением изобары и выражает известный закон Шарля. Для описания изобарических процессов вводится коэффициент объёмного расширения газа a, который определяется следующим образом:

.

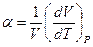Изохорический процесс

Процесс, происходящий в газе при постоянном объёме, называют изохорическим процессом. Для получения уравнения изохорического процесса представим выражение (1.2) в виде

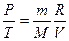. (1.8)

При постоянном объёме и массе газа из (1.8) следует, что отношение P/T остаётся постоянным:

.

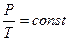Это выражение закона Гей – Люсака.

Закон Авогадро

Пусть имеем два одинаковых объёма двух различных газов при одинаковых давлениях и температурах. Для каждого из них можно записать уравнение состояния в форме (1.4)

,

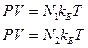где N₁ и N₂ – число молекул в каждом из объёмов. Из этих двух равенств следует N₁= N₂. Это есть и закон Авогадро, который формулируется следующим образом: при одинаковых давлениях и температурах в равных объёмах любого газа содержится одинаковое число различных молекул.

Из этого закона следует, что и наоборот, различные газы, содержащие одинаковое число молекул, будут при одинаковых давлениях и температурах занимать одинаковые объёмы. Поэтому грамм-молекула любого газа при данном давлении и температуре занимает одинаковый объём. В частности, при 0^о С и при давлении в 1 атм 1 моль любого газа будет занимать объём

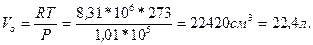
Легко вычислить и число n₀ молекул газа в объеме 1см³ при этих, так называемых, нормальных условиях

n_o= .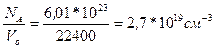

Это число называется числом Лошмидта.

Закон Дальтона

Пусть в сосуде с объёмом V находится в термическом равновесии смеси различных химически не реагирующих друг с другом газов. Для такой смеси уравнение состояния имеет вид 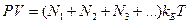, где N₁, N₂, N₃,… - числа молекул соответствующих компонентов смеси. Очевидно, что N₁ + N₂ + N₃ + … = N, где N – общее число молекул в сосуде. Давление смеси газов равно:

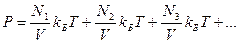
Это выражение показывает, что каждая группа молекул оказывает давление, не зависящее от того, какое давление оказывают другие молекулы. Это обусловлено тем, что в идеальном газе между молекулами нет взаимодействия, молекулы «не знают» о существовании других молекул.

Выражения 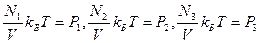называют парциальными давлениями. Парциальным давлением какого-либо газа – компонента газовой смеси называется давление, которое оказывал бы этот газ, если бы он занимал весь объём занимаемый смесью.Таким образом

,

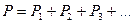т. е. давление смеси газов равно сумме парциальных давлений её компонент. Это есть содержание закона Дальтона.

В конце отметим, что с точки зрения термодинамики, газ, подчиняющийся всем перечисленным выше законам, называется идеальным газом. Реальный газ по своим свойствам близок к идеальному газу при высоких температурах и низких давлениях.