III. Уравнение стоячей волны
Рассмотрим теперь стоячие волны, являющиеся результатом интерференции двух одинаковых волн, бегущих навстречу друг другу. Такие волны чаще всего образуются при наложении волн, падающих на границу раздела сред и отраженных от нее. Например, если взять источник звука (динамик) и расположить его на некотором расстоянии от отражающей стены, то при подаче на динамик напряжения синусоидальной формы последний будет излучать продольные бегущие волны. Достигнув стенки, волны отражаются и, распространяясь в обратном направлении, налагаются на волны, исходящие от непрерывно колеблющегося диффузора динамика. Благодаря этому, каждая точка среды между источником и стенкой будет участвовать в двух колебаниях. Результирующее смещение всех точек среды можно найти путём алгебраического сложения смещений, так как они происходят вдоль одной прямой. В нашем примере отражение происходит от среды более плотной. Тогда деформация сжатия, достигающая стенки, не может привести ее в движение, поэтому за сжатием в падающей волне будет следовать сжатие в отраженной волне, за разряжением в падающей - разряжение в отраженной волне. Следовательно, в точке у самой границы волны суммируются в одной фазе, а так как длины обеих волн одинаковы, то и в остальных точках колебания складываются также.
Рассмотрим случай, когда отраженная волна имеет ту же амплитуду, что и падающая:
 ,
,
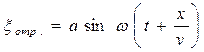 (6)
(6)
Результирующая волна:
 (7)
(7)
Последнее уравнение является уравнением стоячей волны. Величина 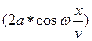 не зависит от времени и является амплитудой и зависит от координаты точки. Иными словами, амплитуды колебаний различных точек различны. Точки, в которых амплитуда максимальна 2а, называются пучностями. Точки, в которых амплитуда равна нулю, называются узлами. Так как при отражении от более плотной среды граничная точка в колебании не участвует, то этой точке будет соответствовать узел.
не зависит от времени и является амплитудой и зависит от координаты точки. Иными словами, амплитуды колебаний различных точек различны. Точки, в которых амплитуда максимальна 2а, называются пучностями. Точки, в которых амплитуда равна нулю, называются узлами. Так как при отражении от более плотной среды граничная точка в колебании не участвует, то этой точке будет соответствовать узел.
Координаты узлов можно найти из уравнения: 
Тогда  где n=0,1,2.
где n=0,1,2.
Следовательно, координаты узлов: 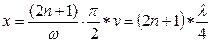 .
.
Расстояние между соседними узлами 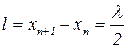 .
.
Координаты пучностей можно найти из уравнения: 
Тогда  , где n = 0, 1, 2, … .
, где n = 0, 1, 2, … .
Следовательно, координаты пучностей: 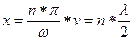 .
.
Расстояние между соседними пучностями 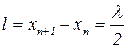 .
.
Амплитуда 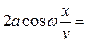
 при переходе через нулевое значение меняет знак, поэтому фаза колебаний по разные стороны от узла отличается на π. Все точки, находящиеся между двумя соседними узлами, колеблются в одной фазе.
при переходе через нулевое значение меняет знак, поэтому фаза колебаний по разные стороны от узла отличается на π. Все точки, находящиеся между двумя соседними узлами, колеблются в одной фазе.
Если волна распространяется на участке среды, ограниченной с двух сторон, то стоячая волна имеет узлы на обеих границах. Поэтому на этом участке образуется целое число полуволн. Когда обе границы свободны, на них образуются пучности. На таком же участке также укладывается целое число полуволн. В случае участка, ограниченного с одной стороны и свободного с другой стороны (например, в опыте Квинке, где трубка с воздухом закрыта с одной стороны), на первой границе – узел, на второй – пучность. В этом случае на участке укладывается нечетное число полуволн.
IV. Резонанс звуковых колебаний.
Образование стоячих волн тесно связано с возникновением резонанса. Усиление звуковых колебаний, т.е.резонанс, может наблюдаться в телах конечных размеров в результате наложения многократно отраженных волн. Усиление звуковых колебаний будет иметь место только в том случае, если волны одного направления находятся в фазе с волнами встречного направления, являющимися отражением первых. Такие условия в указанных телах наблюдаются только для определенных частот колебаний, носящих названия собственных частот колебаний тела. Собственные частоты колебаний определяются размерами тела, его механическими свойствами (плотностью, упругостью), а также выбором неподвижных точек (условием закрепления) и свойствами окружающей среды (условиями на границе). На рис.3, изображены собственные (резонансные) колебания газа в открытой с одного конца акустической трубе длиной L.
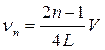 |  |
| Рис.3 |
Штриховой кривой изображено распределение смещения. При длине столба, равной 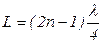 , в нем возникает резонанс. Если изменить длину резонирующего столба на величину l/2, то полученный столб также будет резонировать. Таким образом, наименьшая разность двух воздушных столбов, в которых возникает резонанс, равна:
, в нем возникает резонанс. Если изменить длину резонирующего столба на величину l/2, то полученный столб также будет резонировать. Таким образом, наименьшая разность двух воздушных столбов, в которых возникает резонанс, равна:
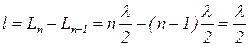 , (9)
, (9)
откуда
 (10)
(10)
Подставляя значение l из последнего выражения в (5), получим: 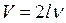 .
.
В данной работе частота задается источником звука - звуковым генератором. Поэтому скорость звука можно определить, непрерывно уменьшая (увеличивая) длину воздушного столба и отмечая разность между двумя последовательными максимумами (минимумами) звучания.
V. Сложение взаимно перпендикулярных колебаний.
Если материальная точка совершает одновременно колебания вдоль оси х и вдоль оси у, то форма криволинейной траектории, по которой движется эта точка, зависит от разности фаз обоих колебаний.
Выберем начало отсчета времени так, что начальная фаза колебаний вдоль оси х равна нулю, тогда уравнение колебаний материальной точки можно записать следующим образом:
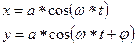
После несложных преобразований уравнение траектории движения материальной точки примет вид:
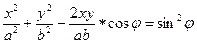 (11)
(11)
Если 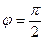 , то это уравнение примет вид:
, то это уравнение примет вид: 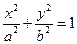 - это уравнение эллипса.
- это уравнение эллипса.
Если 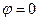 или π, уравнение преобразуется следующим образом:
или π, уравнение преобразуется следующим образом:  или
или 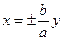 - это уравнение прямой.
- это уравнение прямой.
Задания и указания к выполнению работы:
Задание 1: Определить скорость звука в воздухе методом резонанса (методом Квинке).
Принадлежности: звуковой генератор, телефон, прибор Квинке.
Рассмотрим условие резонанса колебаний воздуха в трубе, закрытой с одного конца.
Покажем, что, если длина столба равна  , то в нем возникает
, то в нем возникает
резонанс.
Действительно, при отражении у закрытого конца трубы образуется узел. Расстояние между двумя соседними узлами, как мы видели ранее, равно l/2 , а, следовательно, при длине столба равной  , на открытый конец приходится пучность стоячей волны - падающей волны (рис.5). Пусть волна, вышедшая из открытого конца, доходит до закрытого и отражается (отражение от более плотной среды), потом отражается вторично, уже от открытого конца, но уже с меньшей амплитудой и т.д.
, на открытый конец приходится пучность стоячей волны - падающей волны (рис.5). Пусть волна, вышедшая из открытого конца, доходит до закрытого и отражается (отражение от более плотной среды), потом отражается вторично, уже от открытого конца, но уже с меньшей амплитудой и т.д.
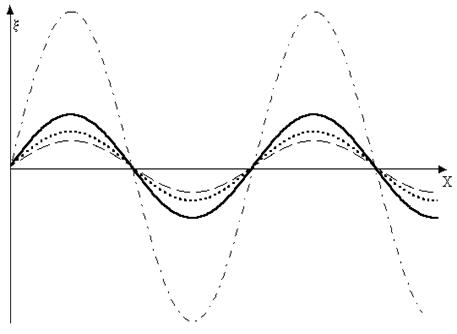 |  - падающая волна - падающая волна | |
 - отраженная волна - отраженная волна | ||
 - вторично отраженная волна - вторично отраженная волна | ||
 - результирующая волна - результирующая волна | ||
| Рис.4 |
Отраженная волна будет находиться в фазе с падающей, т.е. будет её усиливать. Вследствие многократных последующих отражений амплитуда стоячей волны резко возрастает - наступит резонанс. Если соотношение 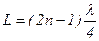 не выполняется, то амплитуда колебаний в пучностях не наибольшая, хотя звук и слышен, но не очень громкий.
не выполняется, то амплитуда колебаний в пучностях не наибольшая, хотя звук и слышен, но не очень громкий.
Экспериментальная установка изображена на рис.5.
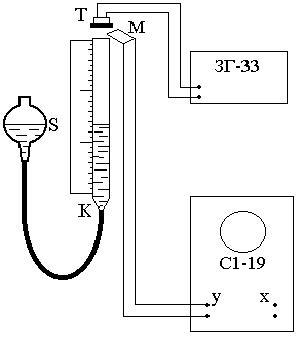 |
| Рис.5 |
Здесь К - длинная стеклянная трубка с миллиметровой шкалой, сообщающаяся резиновым шлангом с сосудом S. Над отверстием трубы К расположена телефонная трубка Т. Катушки электромагнита телефонной трубки Т подключены к выходным клеммам звукового генератора ЗГ-33. Когда возбужденный генератором ток протекает через катушки телефонной трубки, её мембрана приходит в вынужденные колебания и начинает издавать звук. Звуковые волны, распространяясь в трубе K, отражаются от поверхности воды.
Перемещая уровень воды либо вверх, либо вниз, можно добиться резонанса, т.е. максимального звучания воздушного столба, заключенного в трубке. Длину звуковой волны можно измерить, зная расстояние l, на которое должен перемещаться уровень воды в трубке при переходе от одной точки с максимальным звучанием к следующей.
Указания к выполнению работы:
1. Определить скорость звука для 2-3-х частот по указанию преподавателя.
2. Результаты измерений занести в таблицу:
| u1 | u2 | ||||||
| № п/п | L (см) | l/2 (см) | Dl/2 (см) | L (см) | l/2 (см) | Dl/2 (см) | |
| 1. | |||||||
3. Дать окончательный результат скорости звука с указанием погрешности измерения.
Примечание:при определении положений резонанса будьте внимательны! Телефон даёт вторую гармонику (частота 2u), на которой также наблюдается слабый резонанс. Измерения, соответствующие этим гармоникам, исключить из экспериментальных данных. Для определения момента появления резонанса лучше использовать микрофон, подключенный к осциллографу, что поможет выделить нужную частоту.
Задание 2:Определить скорость звука в воздухе методом сложения взаимно-перпендикулярных колебаний.
Принадлежности: звуковой генератор, динамик, микрофон, оптическая скамья, осциллограф.
Скорость звука можно определить из соотношения (5)(см. сведения из теории). Частота колебаний задается внешним источником звука и может быть найдена по положению лимба генератора звуковых частот.
Длина волны по определению равна минимальному расстоянию между двумя точками, колеблющимися в одинаковой фазе. Таким образом, вся задача по нахождению скорости звука в воздухе сводится к отысканию колеблющихся в фазе точек пространства. Такие точки можно отыскать, воспользовавшись методом сложения взаимно-перпендикулярных колебаний. На рис. 8 представлен результат сложения взаимно-перпендикулярных колебаний одинаковой частоты, амплитуды, но разных фаз.
В данной работе складываются два взаимно-перпендикулярных колебания от генератора ЗГ-33 и микрофона М (рис.6). В качестве источника звука берется динамик Д, который питается от звукового генератора. На месте приёмника располагается микрофон М. Звуковые волны, дойдя до микрофона, приводят в колебание его мембрану, в результате чего в нем возникают электрические колебания, частота которых равна частоте электрических колебаний, подаваемых на динамик. Электрические колебания, создаваемые микрофоном и звуковым генератором, подводятся к электронному осциллографу ЭО на входы Х и У. Электронный луч, участвуя в двух взаимно-перпендикулярных колебаниях с одинаковой частотой, будет описывать на экране различные траектории (фигуры). Вид этих фигур будет зависеть от разности фаз (см. уравнение (11)) электрических колебаний, подаваемых от микрофона и звукового генератора.
Разность фаз, в свою очередь, зависит от расстояния L, между динамиком и микрофоном. Если это расстояние менять, то формы фигуры будет меняться. Когда фигура представляет собой отрезок прямой линии, расположенный в 1 и 2 четвертях, то точки звуковой волны, соответствующие положению микрофона, колеблются в фазе с точками пространства, где находится динамик. При увеличении расстояния между динамиком и микрофоном на длину звуковой волны, разность фаз колебаний, подаваемых на осциллограф, увеличивается на 2p.
 |
| Рис.6 |
Следовательно, мы снова получим ту же фигуру Лиссажу. Таким образом, наименьшее расстояние между соседними положениями микрофона, при котором на экране ЭО получается одна и та же фигура Лиссажу, является длиной волны звука в воздухе. Если при увеличении расстояния между динамиком и микрофоном, данная фигура Лиссажу повторится n раз, то расстояние между первым а1, и последним а2 положением микрофона 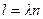 . Подставляя значение l в формулу (5) будем иметь:
. Подставляя значение l в формулу (5) будем иметь:
 .
.
Указание к выполнению работы:
Определить скорость звука для двух - трех частот, указанных преподавателем (в пределах от 1000 Гц до 3000 Гц).
ЛАБОРАТОРНАЯ РАБОТА №11
