Моделирование сезонных и циклических колебаний временных рядов
Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания.
1 ПОДХОД. Расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Общий вид аддитивной модели: Y=T+S+E (Т - трендовая компонента, S - сезонная, Е - случайная).
Общий вид мультипликативной модели: Y=T-S-E
Выбор модели на основе анализа структуры сезонных колебаний (если амплитуда колебаний приблизительно постоянна – аддитивная, если возрастает/уменьшается – мультипликативная).
Построение моделей сводится к расчету значений T,S,E для каждого уровня ряда.
Построение модели:
1.выравнивание исходного ряда методом скользящей средней;
2.расчет значений компоненты S;
3.Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (T+E) в аддитивной или (T*E) в мультипликативной модели.
4.Аналитическое выравнивание уровней (T+E) или (T*E) и расчет значения Т с использованием полученного уровня тренда.
5.Расчет полученных по модели значений (T+S) или (T*S).
6.Расчет абсолютных и/или относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок Е для анализа взаимосвязи исходного ряда и др. временных рядов.
2 ПОДХОД. Построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. Например, при моделировании поквартальных данных модель должна включать четыре независимые переменные – фактор времени и три фиктивные переменные. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту временного ряда для какого-либо одного периода. Она равна единице (1) для данного периода и нулю (0) для всех остальных. Недостаток модели с фиктивными переменными – наличие большого количества переменных.
(аналитическое выравнивание временного ряда)
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:
• линейный тренд: 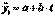
• гипербола: 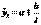
• экспоненциальный тренд: 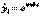
• тренд в форме степенной функции: 
• парабола второго и более высоких порядков: 
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой перемен- 1 ной — фактические уровни временного ряда . 
Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни 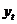 и
и  тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временно м ряде, тем в большей степени будут различаться значения указанных коэффициентов.
тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временно м ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации R2 и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
