Циклические группы
Определение. Группа, составленная положительными и отрицательными степенями одного элемента 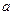 , называется циклической группой.
, называется циклической группой.
Говорят, что элемент 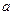 порождает эту группу. Очевидно, что элемент
порождает эту группу. Очевидно, что элемент 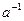 также можно считать порождающим элементом.
также можно считать порождающим элементом.
Определение. Группа называется бесконечной (свободной) циклической, если элементы 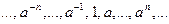 все попарно различны.
все попарно различны.
Определение. Группы  и
и 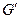 называются изоморфными, если между ними можно установить такое взаимно однозначное соответствие, при котором для любых двух элементов
называются изоморфными, если между ними можно установить такое взаимно однозначное соответствие, при котором для любых двух элементов 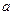 и
и 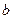 из
из  и соответствующих им элементов
и соответствующих им элементов 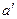 и
и 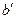 из
из 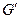 произведению
произведению 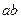 соответствует произведение
соответствует произведение 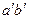 .
.
Примером свободной циклической группы является группа целых чисел относительно сложения. Любая свободная циклическая группа ей изоморфна, изоморфизм задается соответствием 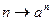 , так как при умножении степеней элемента
, так как при умножении степеней элемента 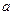 показатели степени складываются.
показатели степени складываются.
Однако среди элементов циклической группы могут встречаться одинаковые. Если 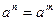 , то
, то 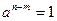 , так что в этом случае некоторая степень с натуральным показателем порождающего элемента равна 1.
, так что в этом случае некоторая степень с натуральным показателем порождающего элемента равна 1.
Определение. Порядком 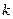 элемента
элемента 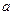 называется наименьший показатель степени такой, что
называется наименьший показатель степени такой, что 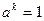 .
.
Если порядок равен числу 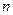 , то среди элементов
, то среди элементов 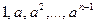 нет равных. Предположим, что
нет равных. Предположим, что 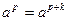 ,
, 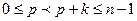 . Тогда
. Тогда 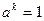 , причем
, причем 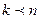 , т. е. порядок элемента равен
, т. е. порядок элемента равен 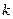 и он меньше
и он меньше 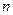 . Всякий элемент
. Всякий элемент 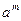 равен одному из элементов
равен одному из элементов 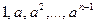 , а именно
, а именно 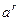 , где
, где 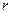 - остаток от деления
- остаток от деления 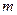 на
на 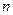 . Таким образом, порядок группы, порожденной элементом порядка
. Таким образом, порядок группы, порожденной элементом порядка 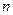 , также равен
, также равен 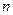 .
.
Пусть  - данная группа. Любой ее элемент порождает некоторую циклическую подгруппу. Если
- данная группа. Любой ее элемент порождает некоторую циклическую подгруппу. Если  - конечная группа, то и все ее циклические подгруппы конечны. Порядок группы делится на порядок любой ее подгруппы, в частности, и на порядок любой циклической подгруппы. Этот порядок равен порядку порождающего элемента. Поэтому верна теорема, которая является следствием из теоремы Лагранжа.
- конечная группа, то и все ее циклические подгруппы конечны. Порядок группы делится на порядок любой ее подгруппы, в частности, и на порядок любой циклической подгруппы. Этот порядок равен порядку порождающего элемента. Поэтому верна теорема, которая является следствием из теоремы Лагранжа.
Теорема. Порядок конечной группы делится на порядок любого ее элемента.
Пусть  - конечная группа порядка
- конечная группа порядка 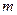 и
и 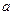 - некоторый ее элемент порядка
- некоторый ее элемент порядка 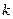 . Тогда
. Тогда 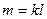 ,
, 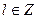 и
и 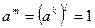 . Отсюда вытекает следующее предложение.
. Отсюда вытекает следующее предложение.
Предложение. Любой элемент конечной группы при возведении в степень, равную порядку группы, дает единицу.
