V7: Система линейных одновременных уравнений

I:

S: При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами

-: состоятельности, смещенности и эффективности

+: состоятельности, несмещенности и эффективности

-: состоятельности, смещенности и неэффективности

-: несостоятельности, смещенности и эффективности

I:

S: Для регрессионной модели вида 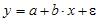построена на координатной плоскости совокупность точек с координатами 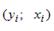, данное графическое отображение зависимости называется

-: параметрами уравнения

-: случайными факторами

-: множественной регрессией

+: полем корреляции

I:

S: Для обнаружения автокорреляции в остатках используется

-: тест Парка

-: тест Уайта

+: статистика Дарбина – Уотсона

-: критерий Гольдфельда – Квандта

I:

S: Величина 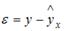называется

-: значением параметра

-: оценкой параметра

-: переменной

+: случайной составляющей

I:

S: Строится эконометрическая модель линейного уравнения множественной регрессии вида

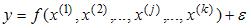(y – зависимая переменная; х(j) – независимая переменная; j = 1,…, k; k – количество независимых переменных). При проверке независимых переменных на отсутствие мультиколлинеарности должно выполняться требование: для любых j и l

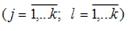абсолютное значение парного коэффициента линейной корреляции

…

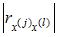-: 0

+: < 0,7

-: > 0,7

-: = 0

I:

S: Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение

-: 0,1

+: 1

-: –1

I:

S: В эконометрической модели линейного уравнения регрессии

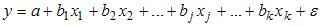коэффициентом регрессии, характеризующим среднее изменение зависимой переменной при изменении независимой переменной на 1 единицу измерения, является

-: xj

-: a

-: y

+: bj

I:

S: Система эконометрических уравнений включает совокупность _________ переменных.

+: эндогенных

-: стационарных

-: постоянных

I:

S: Несмещенность оценок параметров регрессии означает, что …

-: дисперсия остатков минимальная

-: точность оценок выборки увеличивается с увеличением объема выборки

+: математическое ожидание остатков равно нулю

-: дисперсия остатков не зависит от величины

I:

S: Дана автокорреляционная функция временного ряда

Верным будет утверждение, что ряд …

-: содержит только тенденцию, и не содержит сезонной компоненты

-: не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту

+: имеет выраженную сезонную компоненту с лагом 4

-: имеет выраженную сезонную компоненту с лагом 6

I:

S: Если параметр эконометрической модели является статистически значимым, то его значение признается …

-: равным 0

-: равным 1

+: равным коэффициенту парной корреляции

-: отличным от 0

I:

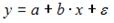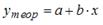S: Для регрессионной модели вида , где рассчитаны дисперсии: 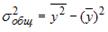; ; 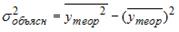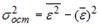. Тогда величина коэффициента детерминации рассчитывается по формуле …

-:

+:

-:

-:

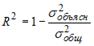
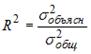
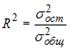
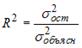
I:

S: Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 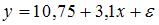. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.

-: 13,85

+: 10,75

-: 7,65

-: 3,1

I:

S: Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …

-:

-:

-:

+:

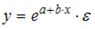
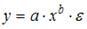
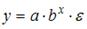
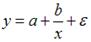
I:

S: Примерами фиктивных переменных в эконометрической модели зависимости стоимости 1 м2 жилья не являются …

-: принадлежность тому или иному региону

-: категория жилья: первичное (новое) жилье / вторичное (неновое) жилье

+: площадь жилья (м2)

I:

S: Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …

+:

-:

-:

-:

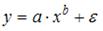
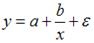
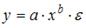
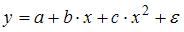
I:

S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …

-:

-:

-:

+:

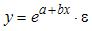
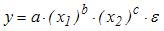
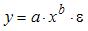
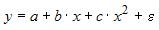
I:

S: По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 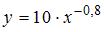, где y – спрос на продукцию, ед.; x – цена продукции, руб. Если фактическое значение t-критерия Стьюдента составляет –2,05, а критические значения для данного количества степеней свободы равны 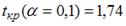, , 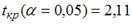, 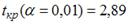то …

-: при уровне значимости 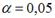можно считать, что эластичность спроса по цене составляет –0,8

-: при уровне значимости 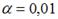можно считать, что эластичность спроса по цене составляет –0,8

-: эластичность спроса по цене составляет –0,8

+: при уровне значимости 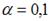можно считать, что эластичность спроса по цене составляет –0,8

I:

S: По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.

-: стохастические и вероятностные

-: линейные и парные

-: множественные и парные

+: линейные и нелинейные

I:

S: Дана таблица исходных данных для построения эконометрической регрессионной модели:

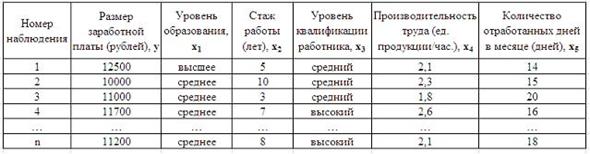
Фиктивными переменными не являются …

+: стаж работы

-: уровень образования

-: уровень квалификации работника

I:

S: При моделировании уравнения множественной регрессии проверку тесноты связи между независимыми переменными (объясняющими переменными, регрессорами, факторами) модели осуществляют на основе …

-: коэффициента множественной корреляции

-: показателей существенности параметров модели

+: матрицы парных коэффициентов линейной корреляции

-: системы нормальных уравнений МНК

I:

S: Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х₁) и уровня безработицы в субъекте (%, х₂) получено уравнение 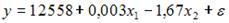. Величина коэффициента регрессии при переменной х₂ свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

-: увеличится на 1,67

-: изменится на (-1,67)

-: изменится на 0,003

+: уменьшится на (-1,67)

I:

S: В модели вида 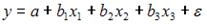количество объясняющих переменных равно …

+: 3

-: 4

-: 1

-: 2

I:

S: В модели множественной регрессии 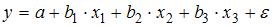определитель матрицы парных коэффициентов корреляции между факторам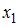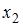и , и 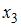близок к нулю. Это означает, что факторы 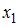, 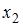и …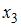

+: мультиколлинеарны

-: значимы

-: независимы

-: количественно измеримы

I:

S: В уравнении линейной множественной регрессии: 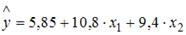, где 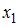– стоимость основных фондов (тыс. руб.); 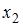– численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х₁, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.

-: на 1 тыс. руб. … уменьшится на 10,8 тыс. руб.

-: на 1% … увеличится на 10,8%

-: на 1 тыс. руб. … увеличится на 10,8%

+: на 1 тыс. руб. … увеличится на 10,8 тыс. руб.

I:

S: Переменная х является нелинейной в уравнении

-:

-:

+:

-:

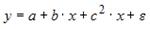
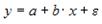
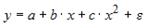
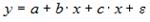
I:

S: Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является

-:

-:

+:

-:

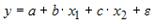
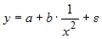
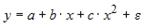
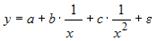
I:

S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной 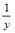. Указанным способом может быть линеаризовано уравнение …

-:

-:

-:

+:

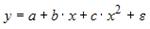
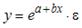
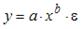
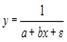
I:

S: Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 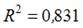(см. рис.).

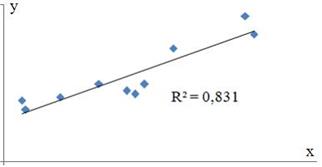
На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.

+: 83,1 %

-: 0,831 %

-: 0,169 %

-: 16,9 %

I:

S: Пусть 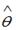– оценка параметра 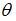регрессионной модели, полученная с помощью метода наименьших квадратов; 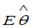– математическое ожидание оценки 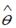. В том случае если 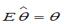, то оценка обладает свойством

+: несмещенности

-: смещенности

-: эффективности

-: состоятельности

I:

S: Степенной модельюне является регрессионная модель …

-:

+:

-:

-:

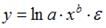
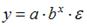
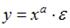
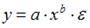
I:

S: Нелинейным уравнением множественной регрессии является …

+:

-:

-:

-:

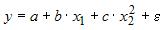
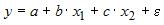
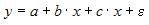
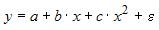
I:

S: Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.

+: бесконечно большого количества

-: трех

-: одного

-: двух

I:

S: В эконометрической модели линейного уравнения регрессии 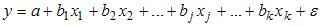ошибкой модели является …

-: a

-: b_j

+:

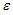
-: x_j

I:

S: Для эконометрической модели линейного уравнения множественной регрессии вида 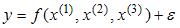построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х⁽¹⁾, х⁽²⁾, х⁽³⁾– независимые переменные):

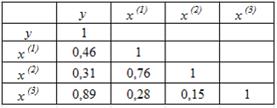
Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …

-: y и x⁽³⁾

+: x⁽¹⁾ и x⁽²⁾

-: x⁽²⁾ и x⁽³⁾

-: x⁽¹⁾ и x⁽³⁾

I:

S: Регрессионная модель вида 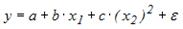является нелинейной относительно …

-: переменной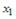

+: переменной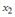

-: параметра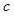

-: переменной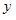

I:

S: Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет

+: 0,8

-:

-:

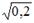
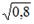
-: 0,64

I:

S: Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками.

-: только гетероскедастичными

-: гомоскедастичными и некоррелированными

+: автокоррелированными и/или гетероскедастичными

-: только автокоррелированными

I:

S: Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.

-: нормальной

+: линейной

-: нелинейной

-: экспоненциальной

I:

S: Автокорреляцией уровней ряда называется корреляционная зависимость между …

-: факторами, формирующими уровень ряда

-: уровнями двух рядов

+: последовательными уровнями ряда

-: компонентами, образующими уровни ряда

I:

S: Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 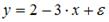является …

-: [0; 1]

-: [–1; 1]

-: [–2; 2]

+: [–1; 0]

I:

S: Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.

-: независимых

+: эндогенных

-: зависимых

-: экзогенных

I:

S: При расчете скорректированного коэффициента множественной детерминации пользуются формулой 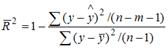, где …

+: n – число наблюдений; m – число факторов, включенных в модель множественной регрессии

-: n – число параметров при независимых переменных; m – число наблюдений

-: n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии

-: m – число наблюдений; n – число факторов, включенных в модель множественной регрессии

I:

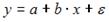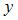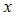S: Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …

-: регрессии

+: корреляции

-: детерминации

-: эластичности

I:

S: Ошибкой спецификации эконометрической модели уравнения регрессии является …

+: использование парной регрессии вместо множественной

-: расчет показателей качества модели

-: учет случайных факторов

-: оценка параметров при помощи МНК

I:

S: В модели множественной регрессии 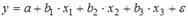определитель матрицы парных коэффициентов корреляции между факторам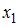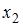и , и 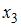близок к единице. Это означает, что факторы 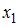, 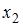и …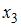

-: мультиколлинеарны

-: независимы

-: количественно измеримы

+: значимы

I:

S: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …

-: автокорреляционной функцией

-: тенденцией

+: временным рядом

-: коррелограммой

I:

S: Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …

-: между трендовой, сезонной и случайной компонентами

+: первого, второго, третьего и последующих порядков

-: факторов, формирующих уровень ряда

-: между несколькими временными рядами

I:

S: Уровень временного ряда (y_t) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда формируют следующие значения компонент уровня временного ряда …

-: y_t = 7; T = 6,5; S = 0; E = 0,5

-: y_t = 7; T = -3,5; S = -2; E = -1

+: y_t = 7; T = 3,5; S = 2; E = 1

-: y_t = 7; T = 3,5; S = -2; E = 1