Дифференциальные уравнения соединений

Рассмотрим три вида соединений двух звеньев: последовательное, параллельное и с обратной связью (рис. 1.14).

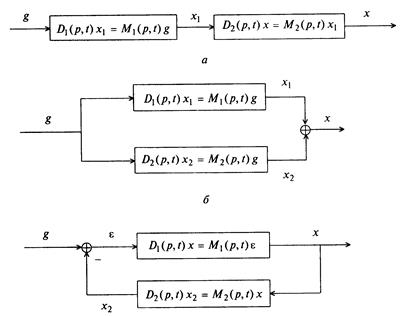
Рис. 1.14

ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ: заданы дифференциальные уравнения звена 1 и звена 2 в операторной форме. Требуется найти дифференциальное уравнение соединения в операторной форме:

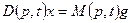. (1.12)

Для решения задачи применим метод уравнивающих операторов [50].

1. Последовательное соединение (см. рис. 1.14,а). Пусть заданы дифференциальные уравнения звеньев 1 и 2 в операторной форме:

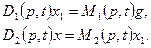(1.13)

Для нахождения дифференциального уравнения последовательного соединения умножим первое уравнение в (1.13) слева на некоторый дифференциаль­ный оператор 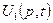, а второе уравнение на 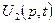. Получим:

,

.

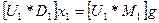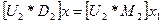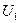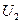Выберем уравнивающие операторы и так, чтобы выполнялось равенство

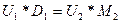. (1.14)

Тогда

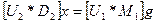, (1.15)

где, сравнивая с (1.12),

, .

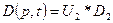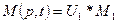Нуги, порядки операторов 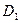, , 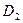, , 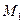, 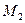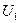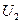равны 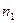, , 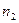, , 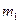, 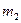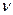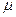. соответственно. Тогда из (1.14) следует равенство порядков операторов в левой и правой части: 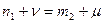. Поэтому можно выбрать 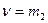, 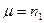и искать уравнивающие операторы в виде

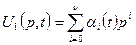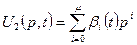, . (1.16)

Общее число неизвестных коэффициентов в (1.16) равно 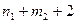, а число уравнений, получающихся в результате приравнивания коэффициентов при одинаковых степенях р в правой и левой части (1.14) составит 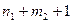. Один коэффициент в процессе решения выбирается произвольно, например .

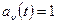При перемножении операторов применяется правило

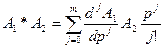, (1.17)

где операторы 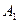, 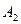имеют порядок соответственно m, n . Если 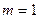, то формула (1.17) имеет вид

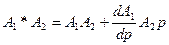. (1.18)

При действии оператора p на функцию, зависящую от аргумент t, производится дифференцирование, например: 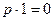, , 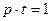, 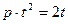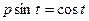и т.д. Для избежания ошибок коэффициенты дифференциальных операторов, равные 1, следует писать явно. Например:

,

,

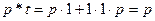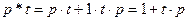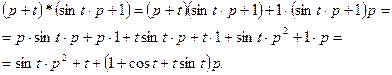
Пример 1.6. Заданы дифференциальные уравнения звеньев

,

.

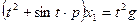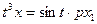Требуется найти дифференциальное уравнение последовательного соединения этих звеньев.

□ Сравнивая с (1.13), имеем 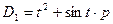, , 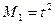, 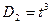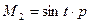. Порядки уравнивающих операторов 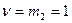, 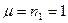и, следо­вательно, они имеют вид 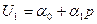, 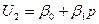. Записываем левую и пра­вую части равенства (1.14), применяя правила (1.17),(1.18):

;

.

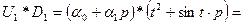
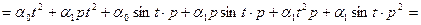
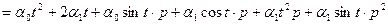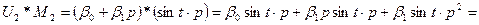
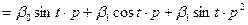Приравнивая коэффициенты при одинаковых степенях р, получаем

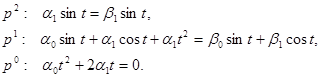
Положим 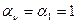. Тогда , , .

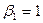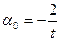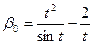Найдем операторы искомого дифференциального уравнения (1.15):

;

.

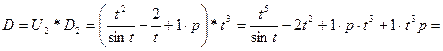
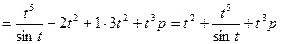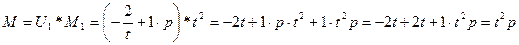Отсюда 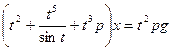, а искомое дифференциальное уравнение имеет вид 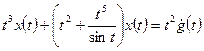или .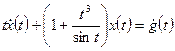

2. Параллельное соединение (см. рис. 1.14,6). Пусть заданы дифференциальные уравнения звеньев 1 и 2 в операторной форме:

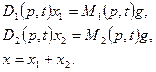
Из второго и третьего уравнений получаем

.

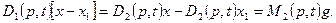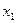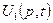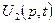Исключим из первого и последнего уравнений. Для этого умножим их слева на уравнивающие операторы и соответственно. Находим

,

.

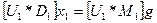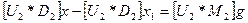Выберем уравнивающие операторы 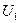и 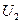так, чтобы выполнялось равенство

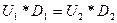. (11.9)

Тогда получаем дифференциальное уравнение параллельного соединения

,

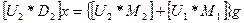а операторы уравнения (1.12) равны

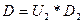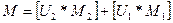, . (1.20)

При этом 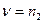, и .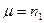

Пример 1.7.Заданы дифференциальные уравнения звеньев I и 2.

,

.

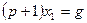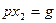Требуется найти дифференциальное уравнение параллельного соединения

этих звеньев.

□ Сравнивая с общей постановкой задачи, имеем 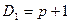, , 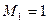, 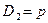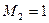. Порядки уравнивающих операторов 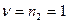, , 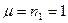по­этому , .

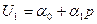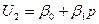Запишем соотношение (1.19):

.

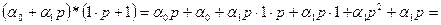
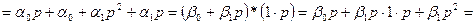
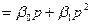Приравнивая коэффициенты при одинаковых степенях р, имеем , , , , , .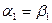

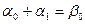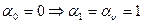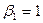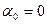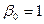Тогда можно записать дифференциальные операторы параллельного соеди­нения в виде (1.20):

;

;

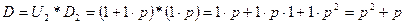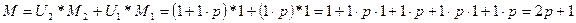а само уравнение — в форме

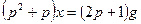или .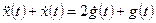

3. Соединение с обратной связью (см. рис. 1.14,в). Пусть заданы дифференциальные уравнения звеньев 1 и 2 в операторной форме, а обратная связь отри­цательная:

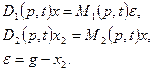
Подставляя третье уравнение в первое, получаем

.

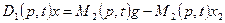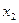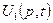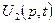Исключим из второго и полученного уравнений. Для этого умножим их слева на уравнивающие операторы и соответственно. Находим

,

.

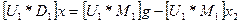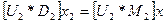Выберем уравнивающие операторы 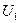, и 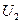так, чтобы выполнялось равенство

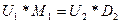. (1.21)

Тогда получаем дифференциальное уравнение соединения с отрицательной обратной связью:

,

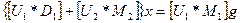а операторы дифференциального уравнения (1.12) равны

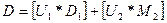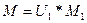, (1.22)

При этом , .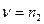

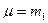Пример 1.8. Заданы дифференциальные уравнения звеньев 1 и 2:

,

.

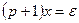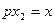Требуется найти дифференциальное уравнение соединения с отрицатель­ной обратной связью.

□ Сравнивая с общей постановкой задачи, имеем 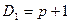, , 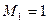, 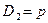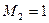. Порядки уравнивающих операторов 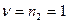, , 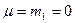по­этому , .

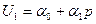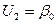Выпишем равенство (1.21) с применением (1.17),(1.18) :

.

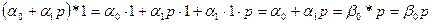Отсюда 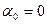, 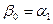. При 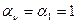имеем 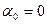, 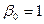. Операторы искомого дифференциального уравнения:

.

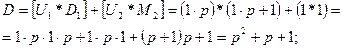
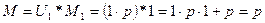Поэтому диференциальное уравнение соединения с обратной связью имеет вид 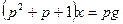или .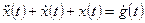

Связь вход-выход

Рассмотрим систему, описываемую дифференциальным уравнением

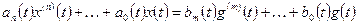; (1.23)

с начальными условиями

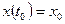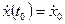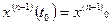, , …, . (1.24)

Требуется по заданному входному сигналу и начальным условиям найти выходной сигнал.

Для линейных систем справедлив принцип суперпозиции, эффект, вызывае­мый суммой нескольких воздействий, равен сумме эффектов каждою из воздействий в отдельности. Поэтому выходной сигнал линейной системы представляется в виде суммы свободного и вынужденного движений:

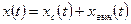. (1.25)

Свободное движение 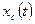происходит при отсутствии внешнего воздейст­вия 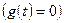вследствие ненулевых начальных условий. Оно является решением однородного дифференциального уравнения, соответствующего исходному урав­нению системы:

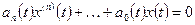(1.26)

с начальными условиями (1.24). В случае, когда начальные условия нулевые, свободное движение в системе отсутствует .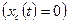

Вынужденное движение 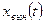происходит вследствие внешнего воздейст­вия 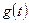при нулевых начальных условиях. Оно является решением неоднород­ного уравнения (1.23) при нулевых начальных условиях. Вынужденное движение 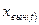отлично от нуля только после приложения внешнего воздействия. Подчеркивая эту причинно-следственную связь, вынужденное движение системы при внешнем воздействии, отличном от нуля при 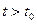, будем обозначать 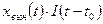, где 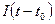— единичная ступенчатая функция (1.2). Выходной сигнал системы будет иметь вид

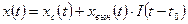, (1.27)

где функции 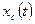, 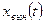можно считать n раз непрерывно дифференцируемыми.

З а м е ч а н и я.

1. Общее решение однородного уравнения (1.26) находится по формуле

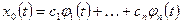, (1.28)

где 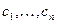— произвольные постоянные; 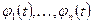— фундаментальная система решений уравнения (1.26).

Если система (1.23) стационарная, т.е. описывается уравнением

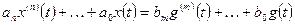
с постоянными коэффициентами, то сначала определяются корни 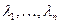характеристического уравнения :

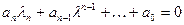. (1.29)

Если корни действительные разные, то (1.28) имеет вид

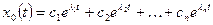. (1.30)

Если среди корней есть кратный действительный корень 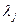кратности к , то ему соответствует следующая составляющая общего решения:

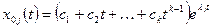. (1 31)

где 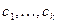— произвольные постоянные.

Паре комплексных сопряженных корней 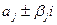соответствует решение

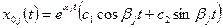, (1.32)

а паре комплексных сопряженных корней кратности k —

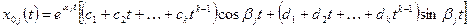, (1.33)

где 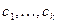; 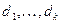— произвольные постоянные.

2. Частное решение неоднородного уравнения (1.23) находится методом вариации произвольных постоянных или методом подбора [40]. В частном случае, когда система описывается уравнением

, ,

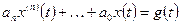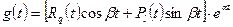где 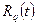, 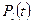— многочлены степеней q и l соответственно, α, β — заданные числа, частное решение ищется в форме

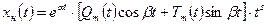, (1.34)

в которой 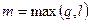, , 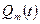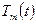— многочлены степени m с неопределен­ными коэффициентами; показатель степени s определяется следующим образом:

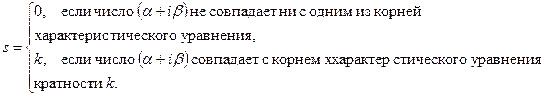
3. Методика решения задачи анализа выходных процессов для стационар­ных систем с помощью перехода от начальных условий к начальным значениям изложена и разд. 3.1.4.

4. По реакции системы на входное воздействие в виде единичной сту­пенчатой функции можно определить основные показатели качества переходных процессов (рис 1.15):

а) статическое отклонение ;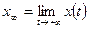

б) максимальное отклонение ;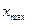

в) время переходного процесса 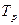— наименьшее время, после которого выполняется услови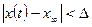е , где 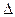— заданная величина;

г) перерегулирование 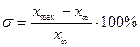, если ;

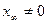д) число колебаний выходного сигнала за время переходного процесса.

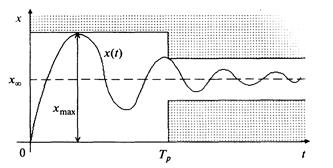
Рис. 1.15

Система управления удовлетворяет требуемому качеству, если все показа­тели качества не превышают заранее заданных значений.

Анализ выходных процессов

ПОСТАНОВКА ЗАДАЧИ

Пусть известны:

а) входной сигнал ;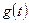

б) система, описываемая дифференциальным уравнением

;

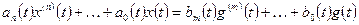в) начальные условия:

, .

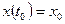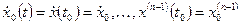Требуется найти выходной сигнал .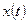

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

1. Найти свободное движение, решив однородное дифференциальное урав­нение (1.26) с заданными начальными условиями (1.24).

2. Найти вынужденное движение, решив неоднородное дифференциальное уравнение (1.23) с нулевыми начальными условиями.

3. Определить выходной сигнал как сумму свободного и вынужденного движений.

Пример 1.9. Найти реакцию системы, описываемой дифференциальным уравнением

, ,

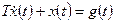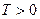на входной сигнал 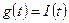при нулевых начальных условиях.

1. Найдем свободное движение. Так как начальные условия нулевые, свободное движение отсутствует, т.е. .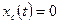

2. Найдем вынужденное движение как решение уравнения 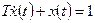при условии :

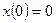а) общее решение однородного уравнения

.

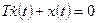Характеристическое уравнение 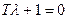имеет корень 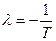. Согласно (1.30)

общее решение однородного уравнения имеет вид ;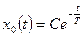

б) частное решение неоднородного уравнения ;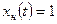

в) общее решение неоднородного уравнения:

;

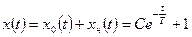г) из начального условия 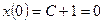следует 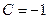. Окончательно

получаем .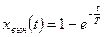

3. Выходной сигнал определяется вынужденным движением

, .

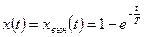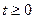Реакция апериодического звена на единичное ступенчатое воздействие изображена на рис. 1.6, в.

Пример 1.10. Найти реакцию колебательного звена, описываемого дифференциальным уравнением

,

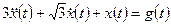на входное воздействие 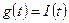при нулевых начальных условиях (здесь ).

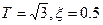1. Найдем свободное движение. Так как начальные условия нулевые, свободное движение отсутствует, т.е. .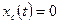

2. Найдем вынужденное движение, которое является решением неоднород­ного дифференциального уравнения 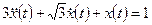при нулевых начальных условиях , :

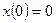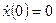а) общее решение однородного уравнения:

.

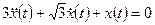Характеристическое уравнение 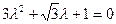имеет корни

.

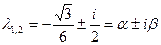
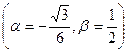Согласно (1.32) общее решение однородного уравнения имеет вид

;

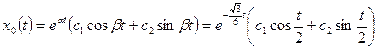б) частное решение неоднородного уравнения: 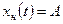. В результате подстановки в неоднородное уравнение имеем ;

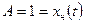в) общее решение неоднородного уравнения:

;

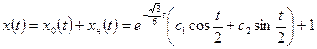г) из начальных условий

,

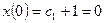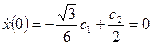
получаем 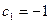, , 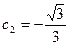а вынужденное движение

.

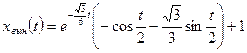3. Выходной сигнал определяется вынужденным движением:

.

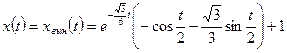Пример 1.11. Найти свободное и вынужденное движения, а также выход­ной сигнал системы, описываемой дифференциальным уравнением

,

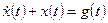с начальным условием 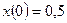при входном сигнале .

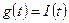1. Определяем свободное движение как решение однородного дифференциального уравнения 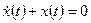при начальном условии .

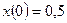Характеристическое уравнение 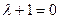имеет корень 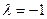. Согласно (1.30) общее решение однородного уравнения имеет вид 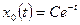. Из начального условия получаем 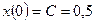, и окончательно свободное движение

.

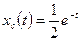2. Находим вынужденное движение как решение неоднородного дифференциального уравнения 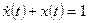при начальном условии :

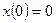а) общее решение однородного уравнения имеет вид 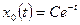(см. п.1);

б) частное решение неоднородного уравнения ищется в виде 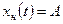. В результате подстановки в неоднородное уравнение имеем , ;

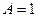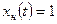в) общее решение неоднородного уравнения:

;

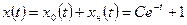г) из начального условия 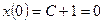следует 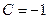. Тогда вынужден­ное движение

.

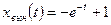3. Выходной сигнал определяется по формуле (1.25):

, .

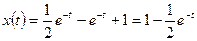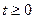Пример 1.12. Найти свободное и вынужденное движения, а также выход­ной сигнал системы, описываемой дифференциальным уравнением

,

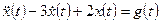с начальными условиями 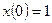, 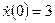при входном сигнале

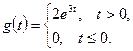
1. Определяем свободное движение как решение однородного дифференциального уравнения 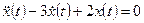при начальных условиях , .

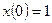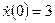Характеристическое уравнение 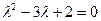имеет два корня: , .

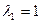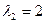Согласно (1.30) получаем общее решение однородного уравнения:

.

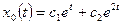Из начальных условий

,

.

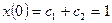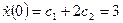имеем 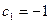, , 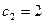а свободное движение

.

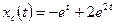2. Находим вынужденное движение как решение неоднородного дифференциального уравнения 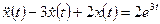при условиях , :

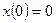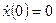а) общее решение однородного уравнения получено в п.1:

;

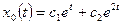б) частное решение неоднородного уравнения 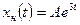. Подставляя в неоднородное уравнение, имеем: 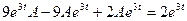. Отсюда , ;

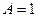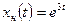в) общее решение неоднородного уравнения:

;

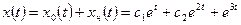г) подставляя в начальные условия, получаем:

,

.

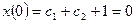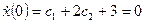Отсюда 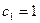, , 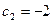а вынужденное движение

.

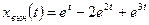3. Выходной сигнал определяется по формуле (1.25):

, .

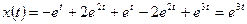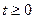Пример 1.13. Найти свободное и вынужденное движения, а также выход­ной сигнал системы, описываемой уравнением

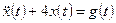
с начальными условиями 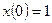, 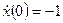при входном сигнале

.

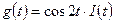□ 1. Определяем свободное движение как решение однородного дифференциального уравнения 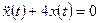при начальных условиях , .

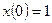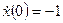Характеристическое уравнение 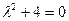имеет два комплексных сопря­женных корня 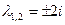( 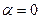, 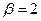). Согласно (1.32) получаем общее решение однородного уравнения:

.

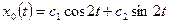Из начальных условий

,

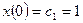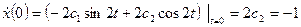
имеем 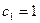, , 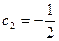а свободное движение

.
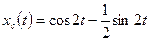