Задание 2. В процессе эксплуатации ЭВМ может рассматриваться как физическая система S, которая в результате проверки может оказаться в одном из следующих состояний: s1 —

В процессе эксплуатации ЭВМ может рассматриваться как физическая система S, которая в результате проверки может оказаться в одном из следующих состояний: s₁ — ЭВМ полностью исправна; s₂ — ЭВМ имеет незначительные неисправности в оперативной памяти, при которых она может решать задачи; s₃ — ЭВМ имеет существенные неисправности и может решать ограниченный класс задач; s₄ — ЭВМ полностью вышла из строя.

В начальный момент времени ЭВМ полностью исправна (состояние s₁). Проверка ЭВМ производится в фиксированные моменты времени t₁ , t₂, t₃. Процесс, протекающий в системе S, может рассматриваться как однородная марковская цепь с тремя шагами (первая, вторая, третья проверки ЭВМ).

1) Составить матрицу переходных вероятностей.

2) Определить вероятности состояний ЭВМ после трех проверок.

В1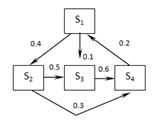
В2
В3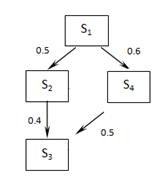
В4
В5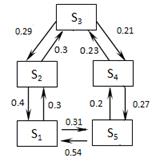
В6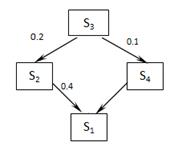
В7
В8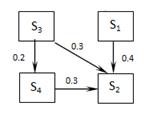
В9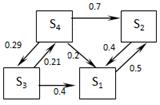
В10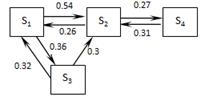

ПРИЛОЖЕНИЕ

Для моделирования цепей Маркова понадобится ряд функций пользователя (Про­граммные модули, реализующие эти функции, представлены на рис. ниже):

1. Функция TrPr(Р, п) вычисляет матрицу переходных вероят­ностей состояний цепи Маркова за п шагов, если матрица переходных вероятностей за шаг есть Р.

2. Безусловные вероятности состояний цепи Маркова на N-м шаге вычисляются функцией UnTrPr(а, Р, п), где а — это вектор вероятно­сти состояний на нулевом шаге.

3. Функция StPr(а, Р, п) вычисляет вероятности состояний для всех п шагов, в предположении, что на нулевом шаге распределе­ние вероятностей состояний есть а.

4. Функция Def(а, х) определяет номер интервала i, в котором содержится число х. Длины интервалов а₀, a₁,... со­держатся и некотором столбце а.

5. Функция ModMCh(а, Р, п, RN) осуществляет де­номинированное моделирование цепи Маркова в течение п шагов, выдавая одну траекторию для заданного вектора RN. В качестве входных переменных используются: вектор а, определяющий начальное распределение вероятностей состоя­ний цепи; матрица Р вероятностей переходов между состояниями за шаг; вектор RN, содержащий п + 1 компоненту RN_i , RN_i < 0 < 1, которые используются при определении состояний цепи Маркова на различных шагах (компонента RN₀ используется для выработки начального состояния цепи согласно распределе­нию а, остальные компоненты — для выработки состояний на шагах 1, 2, п). Эта функция используется в модуле, реализующем основную функцию ImModMCh(а, Р, п, т), которая сама генерирует значение вектора RN. Данный модуль осуществляет имитационное моделирование цепи Маркова в течение п ша­гов. Здесь а, Р, п те же, что и в предыдущей программе, а т — число моделируемых траекторий.

6. Функция ImModMCh в качестве результата возвращает матрицу, стро­ки которой соответствуют номеру шага, а столбцы — номеру реализации. На их пе­ресечении стоит номер состояния на данном шаге в соответствующей реализации.

Пользовательские функции для моделирования цепей Маркова

Группа функций, используемая для анализа поглощающих цепей Маркова:

1.Функция MeanV(Р, т) вычисляет среднее число визитов в невозвратные состояния вплоть до выхода цепи Маркова из множества невозврат­ных состояний. Здесь Р — матрица переходных вероятностей, т — число возвратных состояний. Напомним, что вначале нумеру­ются возвратные состояния, так что первые т строк и столбцов матрицы Р связаны с возвратными состояниями. Последние строки и столбцы описывают ве­роятности переходов между невозвратными состояниями, число которых k - т, где k — общее число состояний цепи. Им соответствует квадратная матрица Q размера k - т. Вышеупомянутое число т находится с помощью функции Dec(Р), которая описывается ниже.

2.Функция AbPr(Р, т) рассчитывает вероятности поглощения в различные воз­вратные состояния, если на начальном шаге цепь Маркова находится в опреде­ленном невозвратном состоянии. В функции используется матрица R, являющаяся подматрицей Р. Столбцы матрицы R соответствуют возвратным, а строки — невозвратным состояниям цепи Маркова, так что эта матрица дает вероятности переходов за шаг из каждого невозвратного в возврат­ное состояние. Результатом работы функции AbPr(Р, т) является матрица, столбцы которой соответствуют т возвратным состояниям, а строки — k - т не­возвратным состояниям. На их пересечении стоит вероятность того, что для цепи Маркова, выходящей из рассматриваемого невозвратного состояния, пер­вым возвратным будет данное состояние.

Заключительные две функции позволяют определять замкнутые классы воз­вратных и класс невозвратных состояний цепи Маркова:

3.Функция Aсс(Р) рас­считывает матрицу достижимости для состояний согласно методу. Строки и столбцы этой матрицы соответствуют состояниям цепь Маркова. На пересечении i-й строки и j-го столбца стоит 1, если состояние j достижимо из состояния i, и 0 — иначе.

4.Функция Dec(Р) для каждого состояния определяет номер замкнутого класса, к которому состояние принадлежит. Исключением здесь являются состояния, ко­торым соответствует нулевой номер класса: эти состояния являются невозврат­ными. Нулевая строка выводимой матрицы содержит номера состояний, а сле­дующая строка — номера классов, к которым принадлежат эти состояния.