Властивості нескінченно малих величин

1. Нескінченно мала величина обмежена.

2. Алгебраїчна сума скінченного числа нескінченно малих величин є нескінченно малою.

3. Добуток нескінченно малої на обмежену або на постійне число є нескінченно малою.

4. Добуток скінченного числа нескінченно малих є нескінченно малою величиною.

Зауваження.Відношення двох нескінченно малих величин може бути величиною скінченною, нескінченно малою і нескінченно великою. Відношення двох нескінченно малих величин являє собою “невизначеність” виду .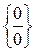

Теорема

Для того, щоб {xn} збігалась до числа а, необхідно і достатньо, щоб an = xn – а була нескінченно малою.

З теореми випливає, що змінну величину {x_n}, яка має границю, можна записати у вигляді суми постійної (границі а) і нескінченно малої:

x_n = a_n + а.

Нескінченно великі величини

Змінна величина xn називається нескінченно великою, якщо для будь-якого як завгодно великого числа M > 0 починаючи з деякого номера N для всіх n > N виконується нерівність xn > M.

Для позначення нескінченно великої послідовності {x_n} використовується такий запис або запис при .

Члени нескінченно великих послідовностей необмежено зростають.

Зауваження. Символ “ 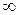” не є числом, тому нескінченно великі послідовності границі не мають. Але прийнято говорити, що нескінченно велика має нескінченну границю, щоб виділити її серед інших послідовностей, що не мають границі, але не є нескінченно великими.

Приклади нескінченно великих: n, n² ,10ⁿ, n!.

Властивості нескінченно великих величин

1. Сума нескінченно великої й обмеженої є нескінченно великою.

2. Сума двох нескінченно великих однакового знаку є нескінченно велика.

3. Добуток двох нескінченно великих є нескінченно великою.

4. Добуток нескінченно великої на сталу додатну величину є нескінченно велика величина.

Зауваження 1.Відношення двох нескінченно великих величин може бути величиною скінченною, нескінченно малою і нескінченно великою. Відношення двох нескінченно великих величин є “невизначеність” виду .

Зауваження 2.Різниця двох нескінченно великих величин може бути величиною скінченною, нескінченно малою і нескінченно великою. Різниця двох нескінченно великих величин являє собою “невизначеність” виду .

Зв'язок між нескінченно великими і нескінченно малими величинами

Якщо x_n – нескінченно мала, то – нескінченно велика. І, навпаки, якщо y_n – нескінченно велика, то – нескінченно мала, (с = const ¹ 0).

Границя функції

Розглянемо функцію , визначену на деякому проміжку Х ÌR . Нехай аргумент х приймає такі значення

х₁, х₂,…,х_n,… (2.2)

де . Відповідні значення функції утворюють:

у₁, у₂,…,у_n,… (2.3)