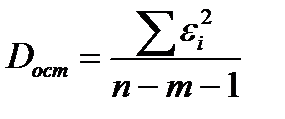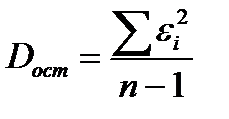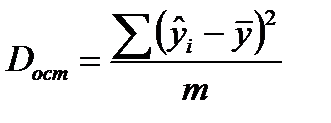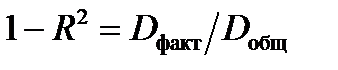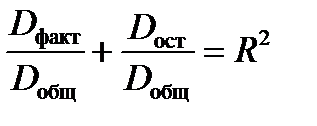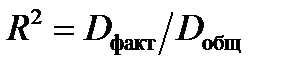O линейный коэффициент корреляции
o множественный коэффициент линейной корреляции
o линейный коэффициент регрессии
o линейный коэффициент детерминации
191. В эконометрических моделях с m независимыми переменными наблюдаемые значения зависимой переменной yi, i=1…n, отличаются от модельных 
на величину εi ( 
). В данных обозначениях формула для расчёта оценки остаточной дисперсии Dост имеет вид:
192. Для общей (Dобщ), факторной (Dфакт) и остаточной (Dост) дисперсий зависимой переменной и коэффициента детерминации R2 выполняется …
193. Для уравнения у=3,14+2х+ε значение коэффициента корреляции составило 2. Следовательно
O значение коэффициента корреляции рассчитано с ошибкой
o теснота связи в 2 раза сильнее, чем для функциональной связи
o связь функциональная
o при увеличении фактора на единицу значение результата увеличивается в 2 раза
194. Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _% дисперсии обусловлено случайными факторами
o 30
o 100
o 70
o 0
195. Доля остаточной дисперсии зависимой переменной у в её общей дисперсии составила 30%, следовательно, величина …
- коэффициента детерминации R2 равна 0,7
- разности (1–R2) равна 0,7, где R2 – коэффициент детерминации
- коэффициента детерминации R2 равна 0,3
- разности (1–R2) равна 0,3, где R2 – коэффициент детерминации
196. Если значение коэффициента корреляции равно единице, то связь между результатом и фактором …
O функциональная
o вероятностная
o стохастическая
o отсутствует
197. Значение F-критерия Фишера зависит только от …
o вида уравнения и числа степеней свободы
o числа переменных
o числа наблюдений
o вида уравнения регрессии
198. Значение коэффициента детерминации составило 0,64. Определите долю случайных факторов в общей дисперсии зависимой переменной
- 0,8
- 0,36
- 0,64
- 64%
199. Значение коэффициента детерминации составило 0,9, следовательно, уравнением регрессии объяснено …
o 10% дисперсии факторного признака x
o 10% дисперсии результативного признака y
o 90% дисперсии факторного признака x
o 90% дисперсии результативного признака y
200. Значение коэффициента детерминации составило 0,9, следовательно, …
- уравнением регрессии объяснено 90% дисперсии результативного признака
- уравнением регрессии объяснено 10% дисперсии результативного признака
- доля дисперсии результативного признака, объяснённая регрессией, в общей дисперсии результативного признака составила 0,1
- доля дисперсии факторного признака, объяснённая регрессией, в общей дисперсии факторного признака составила 0,9
201. Значение коэффициента корреляции может находиться в отрезке
o [–1;1]
o [–1;0]
o [0;1]
o [–2;2]
202. Значение коэффициента корреляции не характеризует