Свойства производной по направлению

1) Производная 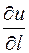определяет величину скорости изменения функции при движении точки М по направлению 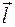. Абсолютная величина производной по направлению определяет величину скорости, а знак производной – характер изменения скорости (ее увеличение или уменьшение).

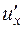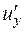2) Производная от функции по положительным направлениям координатных осей Ох, Оу, Оz равны ее частным производным , и 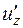. Например, если направление 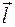совпадает с положительным направлением Ох, то углы, образованные этим вектором и координатными осями Ох, Оу и Оz равны соответственно: α=0, β=g=90°. Тогда, согласно определению, по формуле (1), получим .

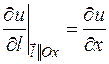3) Производные по прямо противоположным направлениям отличаются только по знаку.

4) Производная по направлению линии уровня (по касательной к линии уровня) функции двух переменных и производная по направлению любой линии, лежащей на поверхности уровня (по любому направлению, касательному к поверхности уровня) функции трех переменных равны нулю.

5) Поле в точке М в направлении 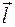возрастает (убывает), если его производная по направлению (соответственно ).

6) Производная по направлению достигает своего наибольшего значения по направлению нормали к поверхности уровня.