Преобразование тригонометрических выражений
5.1. Анализ преобразований.
В тригонометрии существует ряд формул, левая и правая части которых имеют разные области определения. Применение этих формул в процессе решения уравнений приводит к потере корней или к приобретению посторонних. Поэтому такие формулы называют опасными или ненадёжными. Приведём список таких формул.
1. 
2. 
( 
).
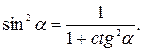3. ( ).
3.1.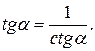 
( ).
3.2. 
4. 5.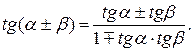 
( 
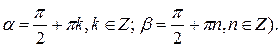
5. 
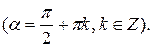
6. 
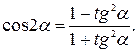
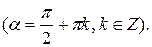
7. 
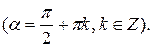
8. 
( 
).
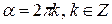9. 
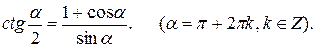
(В скобках указаны числа, расширяющие или сужающие область допустимых значений переменной при переходе от выражения в одной части к выражению в другой части формулы).
Рассмотрим ряд примеров, в которых перечисленные формулы используются в процессе решения уравнения.
Пример 1.Решить уравнение 
Выполним преобразования, не меняющие область определения данного уравнения: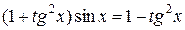 
, 
Далее по формуле 6 получим уравнение 
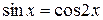с расширенной областью определения. В неё вошли числа вида 
( 
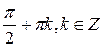), которые могут оказаться посторонними корнями. Следовательно, данное уравнение равносильно системе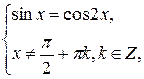 
решая её, получим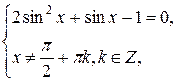 
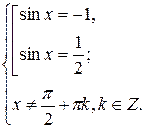
Для решения системы используем окружность (рис. 10).
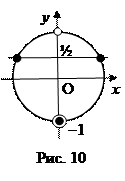
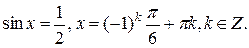
Ответ: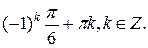 
Применение формулы 6 справа налево привело к расширению области определения данного уравнения и к появлению посторонних решений. Их
отсеивание подстановкой в данное уравнение затруднительно, поэтому целесообразно использовать метод равносильных переходов.
Пример 2. Решить уравнение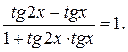 
По формуле 4 данное уравнение может быть записано в виде 
. При этом область определения расширится, так как в неё войдут числа, для которых cos2x = 0. Следовательно, данное уравнение равносильно системе 
, 
которая решений не имеет.
Ответ: решений нет. Покажем на ряде примеров потерю корней уравнения в результате применения перечисленных формул.
Пример 3. Решить уравнение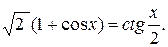 
Область определения данного уравнения: 
Воспользуемся формулой 9, получим уравнение 
с областью определения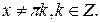 
Применение формулы 9 привело к сужению области определения данного уравнения на числа вида 
, что может явиться возможной причиной потери решений. Подстановкой убеждаемся, что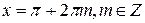 
- решения данного уравнения. Следовательно, оно равносильно совокупности
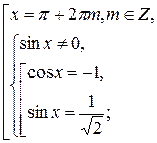
Ответ: 
Пример 4. Решить уравнение 
Область определения данного уравнения составляет множество всех действительных чисел R. Воспользуемся универсальной тригонометрической подстановкой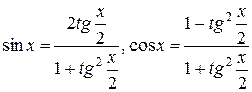 
(формулы 5,6). Получим уравнение 
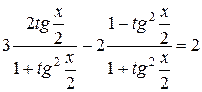, в область определения которого не входят числа вида 
являющиеся корнями данного уравнения. То есть использование формул 5 и 6 слева направо привело к сужению области определения данного уравнения и, как следствие, к потере его корней. Таким образом, данное уравнение равносильно совокупности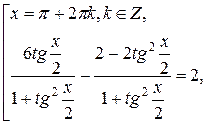 
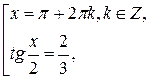
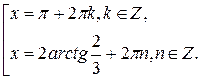
Ответ: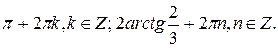 
Пример 5. Решить уравнение 
Область определения данного уравнения задаётся системой
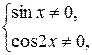
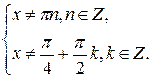
Воспользуемся формулами 5, 7 и 3.2, данное уравнение примет вид 
Его область определения задаётся системой
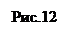
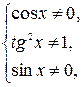
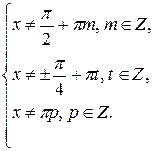
Анализ областей определения данного и полученного уравнения позволяет сделать вывод о её сужении на числа вида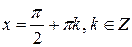 
, которые являются корнями данного уравнения, то есть данное уравнение равносильно совокупности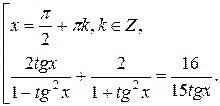 
Решая уравнение совокупности методом замены, получим 
или 
.
Тогда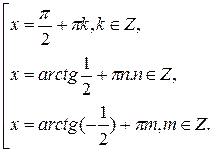 
Ответ: 
5.2. Комплекс заданий
Решить уравнение.
№ 1.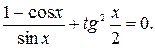 
№ 2. 
№ 3. 
№ 4.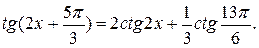 
№ 5. 
№ 6.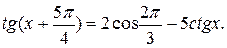 
№ 7.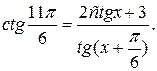 
№ 8. 
№ 9. 
№ 10.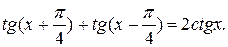 
№ 11.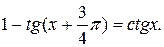 
Ответы:
№ 1.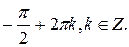 
№ 2.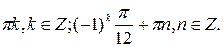 
№ 3.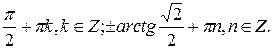 
№ 4.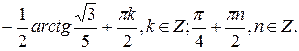 
№ 5. 
№ 6.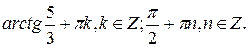 
№ 7. 
№ 8.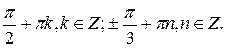 
№ 9. 
№ 10.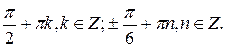 
№ 11.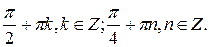 
Приведём таблицу использования формул при решении уравнений составленного комплекса.