Разложения элементарных функций в ряды Маклорена
В этом параграфе мы, используя вид разложения функции в ряд Маклорена
(1) 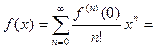
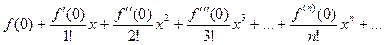 ,
,
найдем разложение по степеням 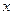 некоторых элементарных функций.
некоторых элементарных функций.
1. Пусть  . Тогда, очевидно,
. Тогда, очевидно, 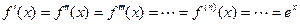 . Поэтому на любом конкретном интервале
. Поэтому на любом конкретном интервале 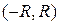 эти производные ограничены одним и тем же числом ( например, числом
эти производные ограничены одним и тем же числом ( например, числом 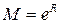 ) и
) и 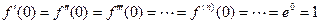 . Поэтому условия теоремы о разложении выполняются на любом интервале
. Поэтому условия теоремы о разложении выполняются на любом интервале 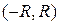 , а потому, согласно (1), для всех
, а потому, согласно (1), для всех 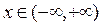 :
:
(2) 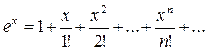 =
= 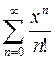 .
.
2. Рассмотрим 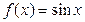 . Тогда
. Тогда  ,
,  ,
, 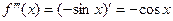 ,
, 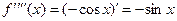 . Поскольку опять получилась функция
. Поскольку опять получилась функция 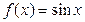 , то дальнейшие производные будут повторять те, что мы уже нашли. Поэтому все производные ограничены на всей числовой прямой (например, числом 1, как все синусы и косинусы) и условия теоремы о разложимости в степенной ряд на всей числовой прямой выполнены. Далее,
, то дальнейшие производные будут повторять те, что мы уже нашли. Поэтому все производные ограничены на всей числовой прямой (например, числом 1, как все синусы и косинусы) и условия теоремы о разложимости в степенной ряд на всей числовой прямой выполнены. Далее, 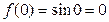 ,
,  ,
, 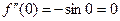 ,
, 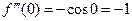 ,
, 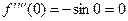 и далее все циклически повторяется. Поэтому разложение (1) будет содержать только нечетные степени
и далее все циклически повторяется. Поэтому разложение (1) будет содержать только нечетные степени 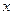 :
:
(3) 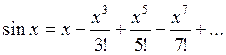 =
= 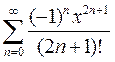
для всех 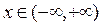 .
.
3. Рассмотрим  . Тогда можно получить разложение в ряд Маклорена тем же путем, что для
. Тогда можно получить разложение в ряд Маклорена тем же путем, что для 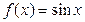 . Но мы сделаем это проще, если учтем полученное разложение (3) для
. Но мы сделаем это проще, если учтем полученное разложение (3) для 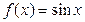 и то, что
и то, что 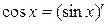 . Дифференцируя (т.е. беря производную) почленно правую и левую части равенства (3), получим, учитывая возможность почленного дифференцирования степенных рядов внутри их интервала сходимости,
. Дифференцируя (т.е. беря производную) почленно правую и левую части равенства (3), получим, учитывая возможность почленного дифференцирования степенных рядов внутри их интервала сходимости,
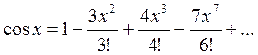
 .
.
Таким образом, для всех 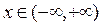 :
:
(4) 

 .
.
4. Рассмотрим 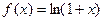 . Тогда, интегрируя почленно полученное ранее разложение
. Тогда, интегрируя почленно полученное ранее разложение 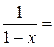
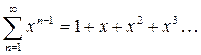 , можно получить
, можно получить
(5) 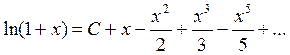 =
= 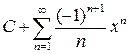
для всех  . Произвольная постоянная
. Произвольная постоянная 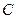 появилась, как обычно, после вычисления неопределенного интеграла. Найдем ее значение. Для этого подставим в (5)
появилась, как обычно, после вычисления неопределенного интеграла. Найдем ее значение. Для этого подставим в (5) 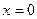 :
: 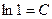 , т.е.
, т.е. 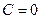 . Поэтому из (5) получаем:
. Поэтому из (5) получаем:
(6) 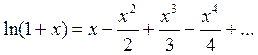 =
= 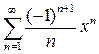 ,
,  .
.
5. Рассмотрим 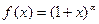 , где
, где 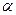 − любое действительное число. Тогда, вычисляя значения производных в нуле, из (1) можно (хотя чуть более громоздко, чем в предыдущих примерах) получить:
− любое действительное число. Тогда, вычисляя значения производных в нуле, из (1) можно (хотя чуть более громоздко, чем в предыдущих примерах) получить:
(7) 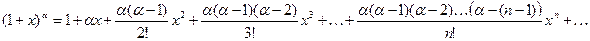 для всех
для всех  . Например, при
. Например, при 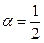 получаем разложение для квадратного корня:
получаем разложение для квадратного корня:
(8) 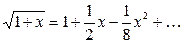 для всех
для всех  .
.
С помощью приведенных выше разложений для основных элементарных можно находить разложения по степеням 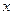 более сложных функций.
более сложных функций.
Пример 1. Разложить по степеням 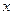 (т.е. в ряд Маклорена) функцию
(т.е. в ряд Маклорена) функцию  .
.
Решение. Заменяя в правой и левой части (6) 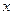 на
на  , получим
, получим
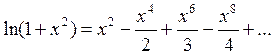 =
= 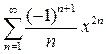 ,
,  .
.
Умножая обе части этого равенства на 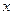 , получаем
, получаем
 =
= 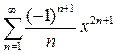 ,
,  .
.
Пример 2. Разложить по степеням 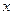 функцию
функцию  .
.
Решение. Применяя формулу понижения степени, получаем
(9) 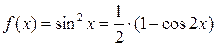 .
.
Подставляя  вместо
вместо 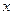 в разложение (4) для косинуса, последовательно для (9) получаем:
в разложение (4) для косинуса, последовательно для (9) получаем:
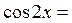
 ,
,
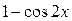
 ,
,

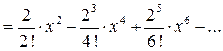
 ,
, 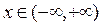 .
.
Пример 3. Разложить по степеням 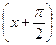 функцию
функцию 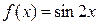 .
.
Решение. Введем новую переменную
(10) 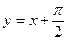
и выразим 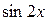 через
через  . Из (10) следует
. Из (10) следует 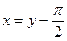 , а потому
, а потому 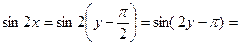 {пользуемся нечетностью синуса}
{пользуемся нечетностью синуса} 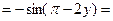 ={пользуемся формулой приведения
={пользуемся формулой приведения 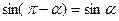 }
}  {в разложение синуса (3) по степеням
{в разложение синуса (3) по степеням 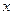 подставляем
подставляем 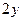 вместо
вместо 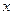 } =
} = 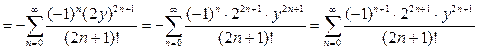 . Подставляя, согласно (10),
. Подставляя, согласно (10), 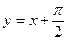 , окончательно получаем:
, окончательно получаем:
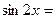
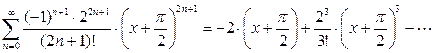 .
.
Это и есть искомое разложение.
С помощью рядов Тейлора и Маклорена можно вычислять приближенные значения функции, обрывая эти ряды на каком-нибудь слагаемом (чем больше оставим членов ряда, тем точнее будет вычисленное значение).
Пример 4. Вычислить приближенно  .
.
Решение. Имеем:  . Из написанного выше в (8) разложения
. Из написанного выше в (8) разложения 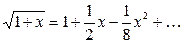 , оставляя 3 слагаемых, получаем приближенную формулу
, оставляя 3 слагаемых, получаем приближенную формулу 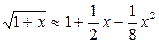 . Применяя ее при
. Применяя ее при 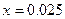 , получим
, получим  . Отметим, что точное значение
. Отметим, что точное значение  .олучим е при _х_ормулу лум (чем больше оставим членов ряда, тем точнее будет вычисленное значение).
.олучим е при _х_ормулу лум (чем больше оставим членов ряда, тем точнее будет вычисленное значение).
Сборник задач по курсу
Элементы теории множеств и математической логики
1. Вставьте пропущенный термин (символ) так, чтобы получилось верное утверждение:
а) множество называется …, если содержит конечное число элементов;
б) запись А...В, означает, что множество А является подмножеством множества В;
 в) символ Æ обозначает … множество;
в) символ Æ обозначает … множество;
2. Соотнесите графическое изображение и
одну из следующих символьных записей: а) DÌ СÌ В
б) ВÌ СÌ D в) CÌ BÌ D
3. Соотнесите текстовую и символьную записи числовых множеств (N, Z, Q, R), заполнив соответствующие клетки следующей таблицы. Приведите примеры чисел, принадлежащих каждому из множеств.
| Множество | Обозначение | Примеры |
| натуральных чисел | ||
| целых чисел | ||
| рациональных чисел | ||
| действительных чисел |
4. Для промежутка на числовой прямой (–4; 3] перечислите списком: а) все натуральные числа, которые принадлежат данному промежутку; б) все целые числа, которые принадлежат данному промежутку.
5. В следующих множествах все элементы, кроме одного, обладают некоторым свойством. Найдите элементы, не обладающие этим свойством:
а) сосна, ель, береза б) 4; 8; 12; 16; 19; 20.
6. Для каждого из слов: сосна, насос, колос, осколок — составьте множества его различных букв, обозначив их соответственно буквами А, В, С, D. Определите, какие из полученных множеств являются равными.
7. Соотнесите символьную запись операции над множествами с ее графическим изображением (результат операции заштрихован). Поставьте знак «+» в нужной клетке таблицы.
|
|
| ||||||||||
| В\A | ||||||||||||
| А\В | ||||||||||||
| АÈВ |
8. Закончите предложение так, чтобы оно было верным, выбрав для ответа один из предложенных вариантов. Если dÎ A∩C, то
а) dÎ A и dÏ С; б) dÏ А и dÎ С; в) dÎ А и dÎ С.
9. Пусть множество А={береза, ель, кедр, осина, пихта, сосна, черемуха}. Составьте множество В — все лиственные, так что ВÌ А. Перечислите списком результат операции А\В.
10. Даны множества D=[–4; 2] и F=[0; 5]. Найдите D È F; D∩F; D\F; F\D. Результаты операций изобразите на числовой прямой.
11. 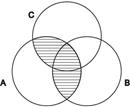 Определите, результат какой операции заштрихован на рисунке. Выберите верный ответ из предложенных и обоснуйте его. а) A∩C∩B
Определите, результат какой операции заштрихован на рисунке. Выберите верный ответ из предложенных и обоснуйте его. а) A∩C∩B
б) A∩C È А∩B
12. Докажите, что если А Ì В и В Ì А, то А = В; если А Ì В, В Ì С, то А Ì С.
13. Установите, истинны или ложны (И, Л) следующие утверждения:
1) пересечение множеств А и В есть множество, состоящее из элементов общих для обоих множеств; 2) если В Ì А, тогда А Ç В = В; 3) если ВÌ А, тогда АÈ В = А;
14. Дан промежуток (–4;3]. Перечислите списком в порядке убывания все натуральные числа, которые принадлежат данному промежутку.
15. Определите, какое из перечисленных множеств является конечным.
1) А=(0; 7); 2) В={4, 5}; 3) С= [4; 5].
16. Какие высказывания истинны: а) 8 делится на 4 б) Крокодил это дерево.
17. Является ли высказыванием уравнение х+4=3 ?
18. Пусть предикат А(х) означает, что студент х из вашей группы является юношей. Истинны ли высказывания: а) 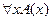 б)
б)  ?
?
19. Истинно ли высказывание  , если
, если 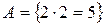 , В={Москва – столица России}?
, В={Москва – столица России}?
Линейная алгебра
1. Пусть 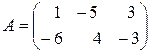 , . А + В = ?
, . А + В = ?
2. , тогда ?
3. Даны матрицы и . Найти матрицу 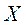 , удовлетворяющую уравнению
, удовлетворяющую уравнению  .
.
4. Пусть  ,
, 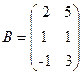 . Тогда
. Тогда 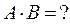
5. Найти миноры и алгебраические дополнения всех элементов матрицы
А =  .
.
6. 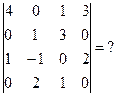
7. 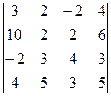 =?
=?
8. Найти обратную для матрицы 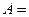
 .
.
9. Решить матричным методом систему  .
.
10. Решить систему  методом Крамера.
методом Крамера.
11. Решить систему методом Гаусса 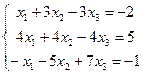 .
.
12. Найти общее решение системы 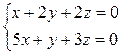 .
.
13. Найти собственные значения матриц: 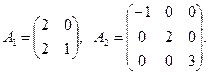
Векторы
1. Даны точки 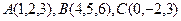 . Найти направляющие косинусы вектора
. Найти направляющие косинусы вектора  .
.
2.  . Найти
. Найти  .
.
3. Найти  и
и  , если
, если 
4.  . Найти значение
. Найти значение  , при котором векторы
, при котором векторы
а) перпендикулярны, б) параллельны.
5.  . Найти угол между векторами .
. Найти угол между векторами .
6. Пусть вершины треугольника расположены в точках А(1,-4,2), В(2,1,1), С(0,4,-1). Найдите площадь треугольника.
7. Найдите угол между медианами треугольника (из предыдущего примера).
8. Пусть 3 вершины параллелограмма расположены в точках А(2,-1,3), В(2,1,1), С(0,4,-1). Найдите его площадь и координату четвертой вершины.
9. Найдите угол между диагоналями параллелограмма из предыдущего примера.
10. Пусть вершины треугольника расположены в точках А(1,-4,2), В(2,1,1), С(0,4,-1). Найдите длину вектора  .
.
Линии на плоскости
1. Найти уравнение прямой, составляющей с осью абсцисс угол 30 градусов и проходящей через точку М(1, 2).
2. Построить прямую с уравнением  .
.
3. Найти координаты точки пересечения прямых с уравнениями 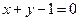 и
и  и угол между ними.
и угол между ними.
4. При каком значении  прямые
прямые 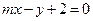 и
и 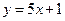 параллельны, а при каком перпендикулярны.
параллельны, а при каком перпендикулярны.
5. Найти уравнение прямой, проходящей через т. М(4, 2) и перпендикулярную прямой  .
.
6. Найти уравнение прямой, проходящей через точку М(2, 3) и точку пересечения прямых 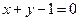 и
и  .
.
7. Найти угол между прямыми 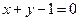 и
и  .
.
8. Найти координаты точки пересечения медиан треугольника с вершинами А(−4,2), В(2, −5),С(5,0).
9. В треугольнике АВС сторона АВ лежит на прямой 3х+у −1=0, сторона ВС лежит на прямой х+3у −22=0, сторона АС лежит на прямой х − у − 2=0, Найти а) угол А; б) уравнение медианы из вершины В; в) уравнение и длину высоты из вершины В.
10. Найти расстояние от точки пересечения прямых 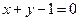 и
и  до прямой
до прямой 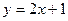 .
.
11. Нарисовать окружность с уравнением 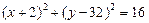 .
.
12. Нарисовать кривую, уравнение которой 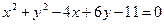 .
.
13. Построить кривую  .
.
14. Построить гиперболу  , найти ее фокусы и эксцентриситет.
, найти ее фокусы и эксцентриситет.
15. Постройте параболу  . Найдите ее фокус и директрису.
. Найдите ее фокус и директрису.
Поверхности и прямые в пространстве
1. Даны точки 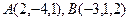 . Написать уравнение плоскости, проходящей через точку
. Написать уравнение плоскости, проходящей через точку  и перпендикулярной вектору
и перпендикулярной вектору 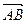 .
.
2. Написать уравнение плоскости, проходящей через точки 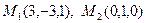 и
и 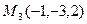 .
.
3. Составить уравнение плоскости, проходящей через точки 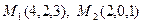 и перпендикулярной к плоскости
и перпендикулярной к плоскости  .
.
4. Составить уравнение плоскости, проходящей через начало координат и параллельной плоскости  .
.
5. Найти расстояние между плоскостью  и плоскостью
и плоскостью 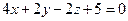 .
.
6. Найти угол между плоскостью  и координатной плоскостью
и координатной плоскостью  .
.
7. Найти уравнение прямой, проходящей через точку М(3,2,1) и параллельной прямой с уравнением  .
.
8. Найти угол между прямой с уравнением  и прямой
и прямой  .
.
9. При каком значении р прямая 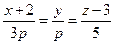 параллельна плоскости
параллельна плоскости 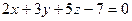 .
.
10. Найти координаты точки пересечения прямой 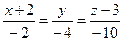 и плоскости
и плоскости 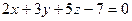 .
.
11. Изобразить поверхность с уравнением  .
.
Пределы и непрерывность функций
1. Найти 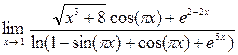 .
.
2. Найти а)  б)
б) 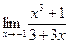 в)
в)  .
.
3. Найти  .
.
4. Найти 1) 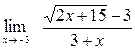 2)
2)  3)
3) 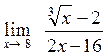 .
.
5. Найти  .
.
6. Найти область определения функции а) 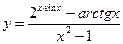 б)
б) 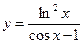 .
.
7. Исследовать на непрерывность функцию 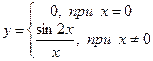 .
.
8. Исследовать на непрерывность функцию:
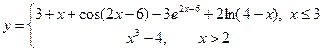 .
.
9. Исследовать на непрерывность следующие функции : а)  ,
,
б) 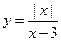 , в)
, в)  , г)
, г) 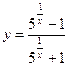 , г) При каком значении
, г) При каком значении 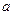 функция
функция  непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Производная функции, ее геометрический смысл
1. Найти по определению значение производной функции y=x3 в точке 2.
2. Найти по определению производную функции y=x3 в произвольной точке.
3. Найти уравнение касательной к графику функции у=х3 в точке с абсциссой, равной (-1) .
4. Найти а) (x7)' ; б)  ; г)
; г) 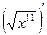 ; д)
; д) 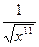 .
.
5. Найти а) 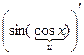 ; б)
; б) 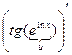 ; в)
; в) 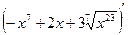 ; г)
; г)  :
:
д) 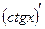 .
.
6. Найти уравнение касательной к графику функции у = 2∙cos(πх) + х2 в точке с заданной абсциссой х0 = 2 .
7. Найти последовательные производные функции f(x)=е2х.
8. Найти вторую производную функции y=x2 e -2x.
Правило Лопиталя. Исследование функций.
1. Найти пределы по правилу Лопиталя: а) 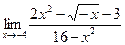 ;
;
б)  ; в)
; в) 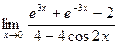 ; г)
; г) 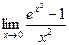 ; д)
; д)  .
.
е)  ; ж)
; ж)  .
.
2. Исследовать на монотонность и экстремум функцию у = х3 – 12х – 1.
3. Найти участки монотонности и экстремумы функции у = х∙е5-х.
4. Найти наибольшее и наименьшее значение функции  на отрезке [1,9].
на отрезке [1,9].
5. Исследовать графики функций на выпуклость и точки перегиба:
а) 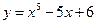 ; б)
; б) 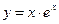 ; в)
; в)  г) у = 2х4 – 24х – 1 .
г) у = 2х4 – 24х – 1 .
6. Найти асимптоты графика функции  .
.
7. Исследовать функцию и построить ее график: а) 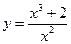 ;
;
б) у=(х-1)е1-х ; в) 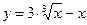 .
.
Функции многих переменных
1. Нарисовать области определения функций:
а)  б)
б) 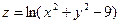 в)
в) 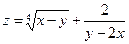 г)
г) 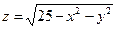
2. Построить линии уровня для функции а)  ; б)
; б)  .
.
3. Найти выражения для обеих частных производных функции z=3x3y2 в произвольной точке М(х,у). Найти z′у(2,2).
4. Доказать, что функция 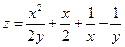 удовлетворяет условию:
удовлетворяет условию:  .
.
5. Найти частные производные функций: а) 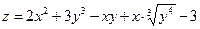
б)  в)
в) 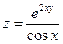 .
.
6. Найти все вторые производные от функции а)z=3x3y2 б) 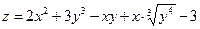 .
.
7. Найти производную функции 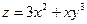 в точке М(1,2) а)по направлению вектора
в точке М(1,2) а)по направлению вектора 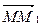 , где М1(3,0), б) по направлению, образующего угол 600 с осью х.
, где М1(3,0), б) по направлению, образующего угол 600 с осью х. 
8. Найти градиент функции 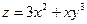 в точке М(1,2).
в точке М(1,2).
9. Найти точки экстремума функций: а) z=7x2+3y2−6xу+2х+6у+3
б) z=10xy − х+3 в) z=x2−xy+4y2+3x−2y+3 г) z=x3 +8y3−6xу +3 д) z=eу(x2+y).
Неопределенный интеграл
1. Вычислить : а) 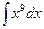 б)
б) 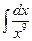 в)
в)  г)
г) 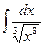 .
.
2. 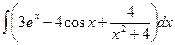 .
.
3. Вычислить интегралы методом непосредственного интегрирования:
а) 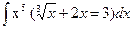 б)
б)  .
.
4. Вычислить интегралы методом внесения под знак дифференциала:
а)  б)
б) 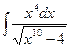 в)
в) 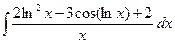 .
.
5. Вычислить интегрированием по частям: а) 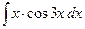 б)
б) 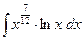
в)  г)
г) 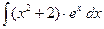 д)
д) 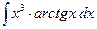
6. Вычислить : а)  б)
б)  в)
в) 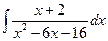
г) 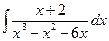 .
.
7. Вычислить : а)  б)
б) 
в)  г)
г)  .
.
8. Вычислить  .
.
9. Вычислить 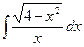 .
.
10. Вычислить  .
.
11. Вычислить 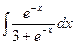 .
.
Определенный интеграл
1. Вычислить а) 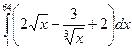 б)
б) 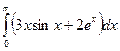 в)
в) 
г) 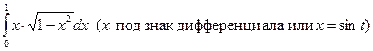 д)
д) 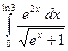 (замена
(замена 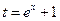 ) е)
) е) 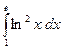 ж)
ж) 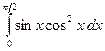 .
.
2. Найти площадь фигуры, ограниченной а) графиками функций y=−3х, y=2x и прямыми х=1 и х=2; б) графиками функций y=х2+х−9, y=2x+3.
3. Вывести формулу  для объема цилиндра высоты H и радиуса основания R.
для объема цилиндра высоты H и радиуса основания R.
4. Найти объем тела, образованного вращением вокруг оси х фигуры, ограниченной а) графиками функций 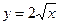 и
и 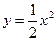 б) графиком функции
б) графиком функции 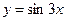 ,
, 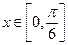 .
.
5. Вычислить несобственные интегралы а) 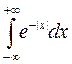 , б)
, б)  .
.
Дифференциальные уравнения
1. Является ли функция 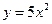 решением дифференциального уравнения
решением дифференциального уравнения 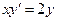 ?
?
2. Найти общее решение уравнения 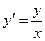 , построить интегральные кривые этого уравнения.
, построить интегральные кривые этого уравнения.
3. Найти решение задачи Коши 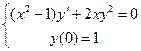 .
.
4. Найти общее решение уравнений (с разделяющимися переменными):
а)  б)
б) 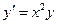 в)
в) 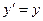 г)
г) 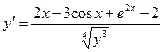 .
.
5. Найти общее решение (или общий интеграл однородных уравнений:
а)  б)
б)  г)
г) 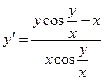 .
.
6. Найти решение задачи Коши  .
.
7. Найти решения линейных уравнений: а) 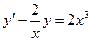 б)
б) 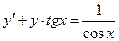 .
.
8. Найти решение уравнения Бернулли  .
.
9. Найти решение задачи Коши  .
.
10. Решить уравнения: а) 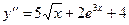 б)
б) 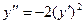 в)
в)  .
.
11. Найти общее решение уравнений:
а) у′′−6у′+5у=0 б) у′′−10у′+25у=0 в) у′′+2у′+2у=0 .
12. Найти общее решение уравнений:
а) у′′−6у′+5у=2х+3 б) у′′−6у′+9у=(х+1)е3х в) у′′+2у′+2у=2ех
г) у′′+2у′+10у=2sinx+3cosx.
Ряды
1. Вычислить  .
.
2. Исследовать сходимость рядов: а) 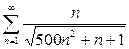 б)
б) 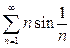 .
.
3. Доказать сходимость рядов (метод сравнения) а)  б)
б)  .
.
4. Исследовать сходимость рядов а)  б)
б) 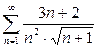
в) 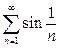 .
.
5. Исследовать сходимость рядов (признак Даламбера) : а) 
б) 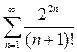 в)
в)  г)
г)  д)
д)  .
.
6. Исследовать сходимость рядов (радикальный признак Коши):
а)  б)
б) 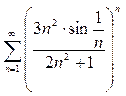 .
.
7. Исследовать сходимость рядов (интегральный признак Коши):
а) 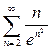 б)
б)  .
.
8. Исследовать ряды на абсолютную и условную сходимость: а) 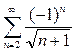
б) 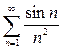 в)
в) 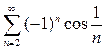 г)
г) 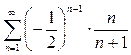 .
.
9. Найти область сходимости функциональных рядов: а) 
б)  .
.
10. Найти область сходимости степенных рядов: а) 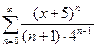
б) 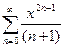 в)
в)  г)
г)  .
.
11. Найти область сходимости и сумму ряда а) 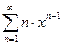 (интегрировать)
(интегрировать)
б)  (дифференцировать).
(дифференцировать).
12. Пользуясь известными разложениями в ряд некоторых элементарных функций, написать разложение по степеням х следующих функций:
а) 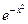 б)
б) 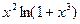 в)
в)  г)
г) 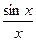 .
.
13. Вычислить приближенно  .
.
Вопросы и задачи для самопроверки
Основы линейной алгебры
1. По какому правилу производится умножение матриц?
2. По какому правилу вычисляются определители матриц? Каковы свойства определителей?
3. Найти определитель матрицы А = 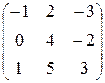 .
.
4. Какие матрицы имеют обратные? Как находить обратную матрицу?
5. Даны матрицы: А =  , В =
, В =  . Найти их произведение. Для матрицы А найти обратную А-1.
. Найти их произведение. Для матрицы А найти обратную А-1.
6. Какими формулами определяется матричный метод решения СЛАУ и метод Крамера?
7. Найти матричным методом и методом Крамера решение следующей системы:  .
.
Векторная алгебра и аналитическая геометрия
8. Как определяется скалярное и векторное произведение векторов? Каковы формулы вычисления скалярного и векторного произведения, угла между векторами по известным их координатам?
9. В пространстве заданы вершины треугольника А(1,–1,0), В(2,1,3) и С(4,0,–3). Найти его углы, площадь, угол между стороной АВ и медианой ВD.
10. Какие имеются виды уравнений прямых на плоскости? Как находить точку пересечения прямых?
11. Как по уравнениям прямых находить угол между ними? Каковы условия перпендикулярности и параллельности прямых?
12. Дана прямая с уравнением 2x + 3y – 6 = 0 и точка М(2,–3). Найти уравнения двух прямых, проходящих через точку М, одна из которых параллельна, а другая перпендикулярна исходной прямой. Найти точку пересечения исходной прямой с перпендикулярной ей прямой.
13. В пространстве заданы вершины треугольника А(1, –1,0), В(2,1,3) и С(4,0, –3). Найти уравнения медианы и высоты треугольника из точки А.
14. Какие существуют виды плоских кривых второго порядка? Каковы их канонические уравнения?
15. Найти уравнение прямой, проходящей через левый фокус эллипса с уравнением 9x2 + 25y2 = 225 и центр окружности с уравнением
x2 + y2 + 4x – 2y – 4 = 0 .
16. Построить гиперболу с уравнением 9x2 – 25y2 = 225 , найти ее эксцентриситет и угол между асимптотами.
17. Как находить уравнение плоскости, перпендикулярной данному вектору и проходящей через данную точку? Как записать уравнение плоскости, проходящей через 3 заданные точки? Каковы условия перпендикулярности и параллельности плоскостей?
18. Найти угол между плоскостью 2x – 3y + 5z – 2 = 0 и координатной плоскостью xOz. Найти уравнение плоскости, содержащей точку М(1,2,3) и параллельной плоскости, проходящей через точки А(1,–1,0), В(2,1,3) и С(4,0, –3).
19. Виды уравнений прямой в пространстве. Как найти углы между прямыми, угол между прямой и плоскостью?
20. Найти угол между прямой и плоскостью, а также точку их пересечения. Прямая задана пересечением плоскостей с уравнениями 2x – 3y + 5z–2 = 0 и 5x – 2y + 3z – 2 = 0, а плоскость имеет уравнение 2x – y + z – 3 = 0.
Пределы, непрерывность, производные функции одного переменного
21. Каковы основные способы раскрытия неопределенностей в пределах?
22. Найти 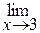
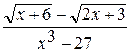 .
.
23. В каких точках непрерывны элементарные функции? Какова классификация точек разрыва функции?
24. Исследовать на непрерывность функцию  .
.
25. Найти наибольшее и наименьшее значение функции y = 2x3 – 15x2 + 36x + 2 на отрезке [0; 2.5].
26. Каков геометрический смысл производной? Как написать уравнение касательной к графику данной функции в известной его точке?
27. Написать уравнения касательных к графику функции y = x2 – 2x + 2 в точках его пересечения с графиком функции y = 3x – 4 .
28. Найти производную функции  .
.
29. В чем заключается правило Лопиталя?
30. Найти 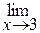
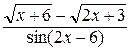 по правилу Лопиталя.
по правилу Лопиталя.
31. Какова схема исследования функции на монотонность и экстремумы?
32. Как находить наклонные и вертикальные асимптоты графика функции?
33. Какова схема общего исследования функции и построения ее графика?
34. Исследовать функцию 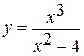 и построить ее график.
и построить ее график.
Функции нескольких переменных
35. Что называется областью определения функции двух переменных?
36. Что такое линия уровня?
37. Построить линию уровня функции z = 4 – x2 – y2 , проходящую через точку А(1;1).
38. Каковы правила нахождения частных производных?
39. Найти частные производные функции  .
.
40. Как вычислить производную функции двух переменных по определенному направлению и ее градиент в заданной точке?
41. Найти градиент и производную функции z = 3x2 + xy – 2y2 + 5 по направлению, составляющему 30о с осью абсцисс, в точке А(2;1).
42. Какова схема нахождения экстремумов функции двух переменных?
43. Найти экстремумы функции z = 6x2 – 7xy + 2y2 + 6x – 3y + 2.
Неопределенный и определенный интеграл
44. Какая функция называется первообразной для данной функции? Сколько первообразных может иметь функция?
45. Что такое метод непосредственного интегрирования?
46. Вычислить  .
.
47. Какие формулы описывают метод замены переменной в неопределенном интеграле?
48. Вычислить 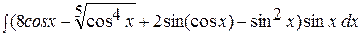 .
.
49. Какой формулой описывается метод интегрирования по частям? Какие классы функций интегрируются этим методом?
50. Вычислить 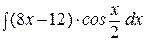 ,
, 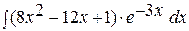 .
.
51. По какой схеме вычисляются интегралы от рациональных функций?
52. Вычислить 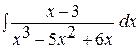 .
. 
53. Какими приемами вычисляются интегралы от тригонометрических функций?
54. Вычислить 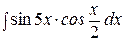 ,
,  .
.
55. Каковы основные приемы интегрирования иррациональных функций?
56. Вычислить 
 ,
,  .
. 
57. Что называется определенным интегралом от функции по заданному интервалу? Какой вид имеет формула Ньютона-Лейбница?
58. Какой вид имеют формулы замены переменной и интегрирования по частям для определенного интеграла?
59. Вычислить 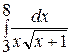 ,
, 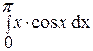 .
.
60. По какой формуле находится площадь фигуры, ограниченной графиками функций?
61. Найти площадь фигуры, ограниченной графиками функций y = 3x – 4 , y = x2 – 2x + 2.
62. Какой формулой выражается объем тела вращения?
63. Вычислить объем тела, полученного вращением вокруг оси абсцисс фигуры, ограниченной графиками функций 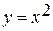 и
и  .
.
64. Как определяется несобственный интеграл с бесконечным верхним пределом?
65. Вычислить 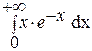 .
.
Дифференциальные уравнения
66. Что такое задача Коши?
67. Какова схема решения дифференциального уравнения 1-го порядка с разделяющимися переменными?
68. Найти решение задачи Коши 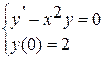 .
.
69. Какова схема решения линейного дифференциального уравнения 1-го порядка?
70. Найти общее решение уравнения  .
.
71. Какие уравнения второго порядка допускают понижение порядка?
72. Найти общее решение уравнения 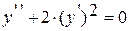 .
.
73. Каковы формулы общего решения линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами?
74. Какой вид имеет общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами? Как находить частное решение в случае правой части специального вида?
75. Найти решение задачи Коши  .
.
Числовые и степенные ряды
76. Какие числовые ряды называются сходящимися? Что называется суммой сходящегося ряда?
77. Каков общий признак расходимости рядов?
78. Исследовать на сходимость ряд 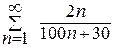 .
.
79. Как формулируется признак сравнения для положительных рядов (в простой и предельной форме)? Какие ряды являются «эталонными»?
80. Исследовать на сходимость ряды 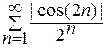 ,
, 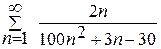 .
.
81. Как формулируются признаки Даламбера и Коши (радикальный и интегральный) сходимости положительных рядов?
82. Исследовать на сходимость ряды 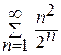 ,
, 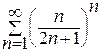 .
.
83. Какие ряды называются знакочередующимися? Как формулируется признак Лейбница сходимости знакочередующихся рядов?
84. Исследовать на сходимость ряд  .
.
85. Какая связь между сходимостью, абсолютной сходимостью и условной сходимостью знакопеременных рядов?
86. Исследовать ряды на абсолютную и условную сходимость  ,
, 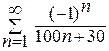 .
.
87. Какой вид имеет область сходимости степенного ряда? Как она ищется?
88. Найти области сходимости степенных рядов 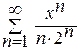 ,
,  .
.
89. Какие функции могут быть разложены в ряд Тейлора? Как вычислить коэффициенты такого ряда? Что такое ряд Маклорена?
90. Какой вид имеют разложения в степенные ряды функций: y = sin(x), y = cos(x), y = ex, y = arctg(x), y = (1+x)m, y = ln(1+x).
91. Разложить функцию y = cos2x по степеням х.