Кусочно-линейная аппроксимация

При использовании степенных полиномов первого порядка кривая в промежутке между двумя известными значениями аппроксимируется отрезком прямой. Такая аппроксимация называется кусочно-линейной. Погрешность при этом будет наибольшей на тех участках изменения функции, где вторая производная достигает наибольшего значения.
При синусоидальной модели сигнала погрешность 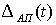будет наибольшей в зоне максимума (рис. 5).

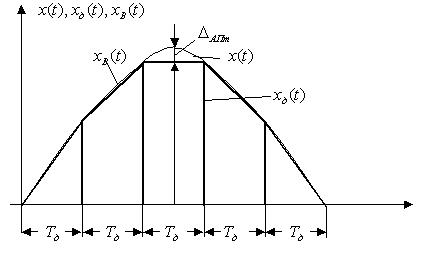
Рис. 5. Погрешность аппроксимации при кусочно-линейной аппроксимации

.

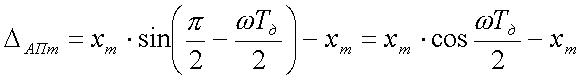(14)

После преобразований в выражении (14) получаем

,

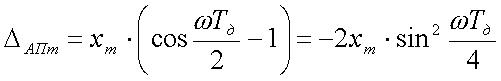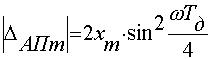
Если принять в виду малости 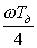, что 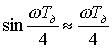, получаем

;

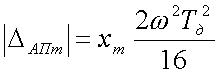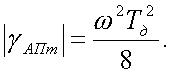
(15)

Тогда требования к частоте дискретизации при заданной погрешности аппроксимации 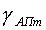при синусоидальной модели сигнала может быть сформулирована следующим образом:

.

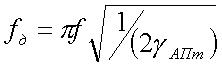(16)

Для 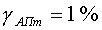получаем

_.

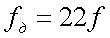Если сравнить результаты расчета 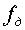для ступенчатой и кусочно-линейной аппроксимации при синусоидальной модели сигнала, то видно, что выигрыш в быстродействии при кусочно-линейной аппроксимации очень большой.

Общий подход к оцениванию суммарной погрешности СИ

При оценивании суммарной погрешности линейного СИ необходимо выполнить следующие этапы (рис.1)

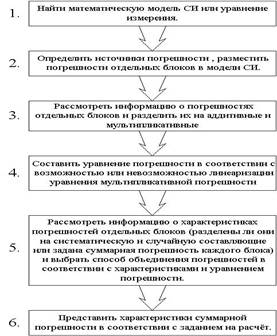
Рис. 1. Этапы оценивания суммарной погрешности СИ

Рассмотрим первый этап оценивания суммарной погрешности СИ. Для удобства СИ представляют в виде структурной модели. В качестве примера рассмотрим структурную схему СИ (рис.2), где Д-датчик с коэффициентом преобразования 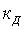, АИП - аналоговый измерительный преобразователь с коэффициентом преобразования 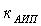, АЦП – аналогово-цифровой преобразователь с уравнением измерения.

,

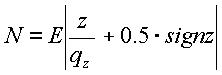(1)

где 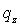- ступень квантования.

Рис.2 Пример структурной схемы СИ

Тогда с учётом того, что блоки Д, АИП линейные, получаем математическую модель СИ или уравнение измерения

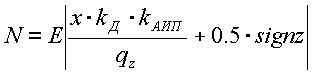
(2)

Используя линеаризацию выражения (2) получаем

,

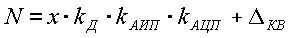(3)

где .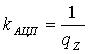
Пренебрегая погрешностью квантования получаем уравнение измерения идеального СИ (без погрешностей):

,

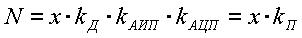(4)

где

.

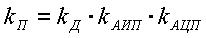(5)

Связь между нормирующими значениями по входу и по выходу представляется в виде

.

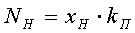(6)

2.11Уравнение погрешности без использования линеаризации

При составлении уравнения погрешности погрешности вводят в математическую модель 2.

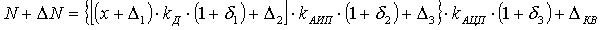
(8)

Тогда абсолютная погрешность СИ равна

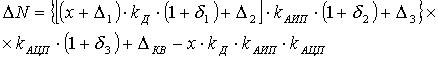
(9)

Относительная погрешность СИ равна

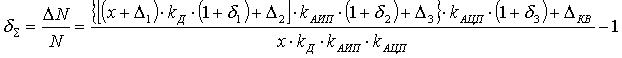
(10)

После преобразований выражения (10) получаем

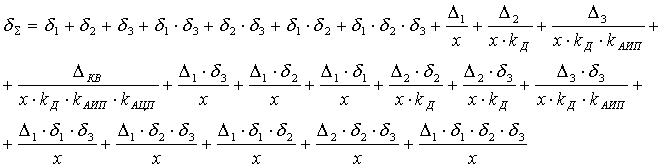
(11)

Если выделить в выражении (11) аддитивную и мультипликативную составляющие

,

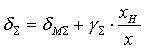(12)

то выражения для мультипликативной составляющей 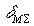и приведенной аддитивной составляющей 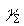имеют вид:

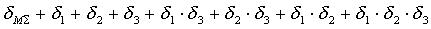
(13)

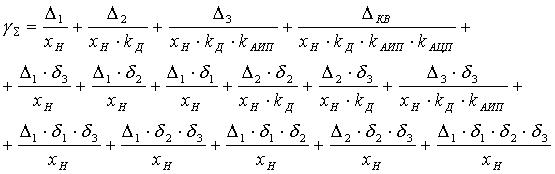
(14)