Метод обращения движения и формула Виллиса

Угловые скорости центральных зубчатых колёс и водило связаны в планетарных механизмах уравнением, которое называют формулой Виллиса. При составлении формулы применяется общее направление отсчёта положительных угловых скоростей основных звеньев, одинаковое для всех звеньев (рис.12.5).

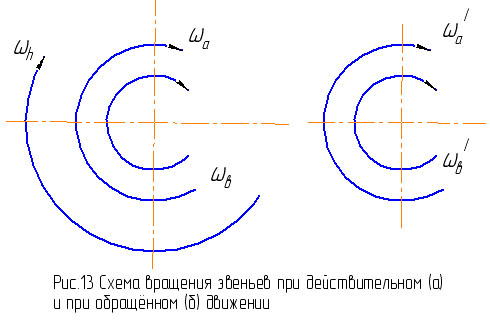
Рис.12.5 Рис.12.6

Если всем основным звеньям планетарного механизма сообщить дополнительное вращательное движение около их общей оси в направлении, противоположном направлению отсчёта угловых скоростей, с угловой скоростью, равной скорости водила, то водило станет неподвижным (рис.12.6), а угловые скорости ω_a^’ и ω_в^’ центральных зубчатых колёс будут определяться по формулам:

ω_a^’ = ω_a - ω_{h ,} ω_в^’ = ω _в - ω_h .

После обращения движения и остановки водила механизм представляет собой многоступенчатую передачу с неподвижными осями зубчатых колёс. В этой передачи передаточное отношение от колеса а колесу в будет определяться по формуле: 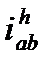= ω_a^’ / ω_в^’ . Подставляя ω_a^’ и ω_в^’ , получаем формулу Виллиса:

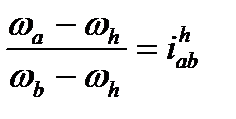(12.1)

Здесь 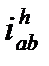- передаточное отношение от колеса a к колесу b при неподвижном водиле, определяемое в зависимости от чисел зубьев зубчатых колёс и с учётом знаков передаточных отношений каждой ступени.

Методика составления формул для определения передаточного отношения планетарной передачи

Определим передаточное отношение i_ah от колеса a к водилу h в планетарной передаче с неподвижным колесом в (рис.12.8). Оно представляет собой отношение угловых скоростей колеса а и водила: i_ah = ω_a / ω _h .

Подготавливаем выражение для нахождения i_ah в зависимости от передаточного отношения при неподвижном водиле, для чего применяем формулу Виллиса. Для удобства практического применения формулы освобождаемся от знаменателя:

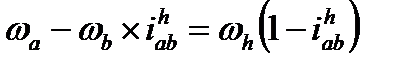
Применительно к нашей расчётной схеме полагаем ω_в =0. Уравнение упрощается. Получаем формулу для определения передаточного отношения в планетарной передаче с одной степенью свободы:

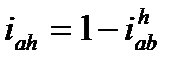(12.2)

Для того чтобы определить передаточное отношение 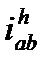при неподвижном водиле в зависимости от чисел зубьев зубчатых колёс, выполняем обращение движения и вычерчиваем кинематическую схему механизма, полученного после обращения движения (рис. 12.9).

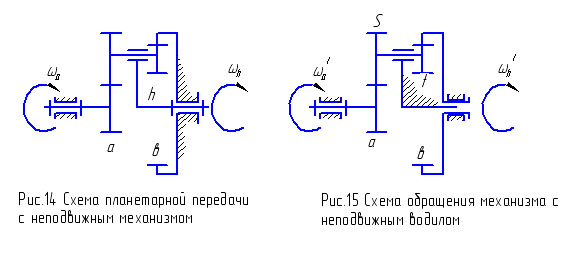
Рис.12.8 Рис.12.9

Этот механизм представляет собой двухступенчатую передачу с неподвижными осями зубчатых колёс, в которой

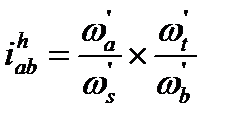, где ω_s^’ и ω_t^’ - угловые скорости сателлитов, ω_s^’ = ω_t^’ .

Заменяем отношения угловых скоростей обратными отношениями чисел зубьев с учётом знаков передаточных отношений:

.

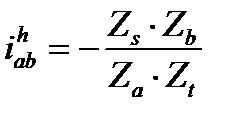Путём подстановки получаем формулу для определения передаточного отношения в планетарной передаче в зависимости от чисел зубьев колёс:

.

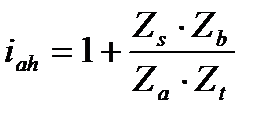Пусть, например, Z_a =16, Z_s=48, Z_t =16, Z_b=80.

Тогда

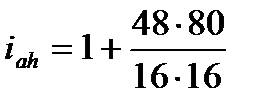= 16 . Передаточное отношение имеет знак «плюс». Следовательно, ведомое звено (в данном случае – водило) вращается в ту же сторону, что и ведущее звено (колесо а ).

Реальные конструкции плоских планетарных передач выполняют состоящими из трёх-четырёх блоков сателлитов (рис.12.10). Это необходимо для обеспечения требуемой нагрузочной способности равномерности распределения нагрузок на опоры.

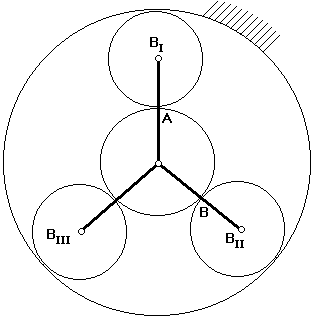
Рис.12.10

При проектировании должны выполнятся следующие условия /1/:

а) условие соосности всех центральных колёс и водила, которые должны иметь общую ось вращения;

б) условие соседства, которое требует, чтобы при многосателлитной конструкции соседние сателлиты не задевали друг друга своими зубьями;

в) условие сборки, которое учитывает одновременного зацепления всех сателлитов с центральными колёсами при симметричности зон зацепления.

Область применения планетарных механизмов.

Планетарные передачи с одной степенью свободы находят большое применение в машиностроении в качестве редукторов и мультипликаторов. Их основное достоинство состоит в том, что при тех же габаритах, что и обычные редуктора, планетарные позволяют передавать значительно большие мощности.

Однако при этом более сложны в изготовлении и монтаже, имеют несколько меньший к. п.д.

Дифференциальные механизмы с двумя степенями свободы находят применение в приборах для суммирования движений, кинематических цепях станков (например, зубофрезерных). Наибольшее применение они имеют в приводах автомобилей. Автомобильный дифференциал позволяет при поворотах автомобиля ведущим левым и правым колёсам вращаться с разными скоростями.