Гармонические электромагнитные колебания

Электрические и магнитные явления неразрывно связаны между собой. Изменение электрических характеристик какого-либо явления влечет за собой изменение его магнитных характеристик. Особую практическую ценность представляют электромагнитные колебания.

Электромагнитные колебания – это взаимосвязанные изменения электрического и магнитного полей, при которых значения величин, характеризующих систему (электрический заряд, ток, напряжение, энергия), повторяются в той или иной степени.

Следует отметить, что между колебаниями различной физической природы существует аналогия. Они описываются одинаковыми дифференциальными уравнениями и функциями. Поэтому сведения, полученнные при изучении механических колебаний, оказваются полезными и при изучении электромагнитных колебаний.

В современной технике электромагнитные колебания и волны играют большую роль, чем механические, так как используются в устройствах связи, телевидения, радиолокации, в различных технологических процессах, определивших научно-технический прогресс.

Электромагнитные колебания возбуждаются в колебательной системе, называемой колебательным контуром. Известно, что любой проводник обладает электрическим сопротивлением R, электроемкостью С и индуктивностью L, причем эти параметры рассредоточены по длине проводника. Сосредоточенными параметрами R, С, L обладают резистор, конденсатор и катушка соответственно.

Колебательным контуром называется замкнутая электрическая цепь, состоящая из резистора, конденсатора и катушки (рис. 4.1). Такая система аналогична механическому маятнику.

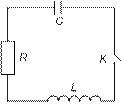Контур находится в состоянии равновесия, если в нем нет зарядов и токов. Чтобы вывести контур из равновесия, необходимо сообщить конденсатору заряд 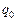(или возбудить индукционный ток 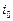с помощью из меняющегося магнитного поля). Тогда в конденсаторе возникнет электрическое поле с напряженностью 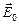. При замыкании ключа К в контуре пойдет ток, в результате конденсатор будет разряжаться, энергия электрического поля уменьшаться, а энергия магнитного поля катушки индуктивности увеличиваться.

Рис. 4.1 Колебательный контур

В некоторый момент времени, равный четверти периода конденсатор полностью разрядится, а магнитное поле достигнет максимума. Это означает, что произошло превращение энергии электрического поля в энергию магнитного поля. Так как токи, поддерживающие магнитное поле исчезли, то оно начнет убывать. Убывающее магнитное поле вызывает ток самоиндукции, который по закону Ленца направлен так же, как ток разряда. Поэтому конденсатор будет перезаряжаться и между его пластинами появится электрическое поле с напряженностью, противоположной первоначальной. Через время, равное половине периода магнитное поле исчезнет, а электрическое – достигнет максимума.

Затем все процессы будут происходить в обратном направлении и через время, равное периоду колебаний, колебательный контур придет в первоначальное состояние с зарядом конденсатора 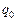. Следовательно, в контуре возникают электрические колебания.

Для полного математического описания процессов в контуре надо найти закон изменения одной из величин (например, заряда) с течением времени, который при использовании законов электромагнетизма позволит найти закономерности изменения всех других величин. Функции, описывающие изменение величин, характеризующих процессы в контуре, являются решением дифференциального уравнения. Для его составления применяют закон Ома и правила Кирхгофа. Однако они выполняются для постоянного тока.

Анализ процессов, происходящих в колебательном контуре, показал, что законы постоянного тока можно применять и для изменяющегося во времени тока, удовлетворяющего условию квазистационарности. Это условие состоит в том, что за время распространения возмущения до самой удаленной точки цепи сила тока и напряжение изменяются незначительно, тогда мгновенные значения электрических величин во всех точках цепи практически одинаковы. Так как электромагнитное поле распространяется в проводнике со скоростью света в вакууме, то время распространения возмущений всегда меньше периода колебаний тока и напряжения.

В отсутствие внешнего источника в колебательном контуре происходят свободные электромагнитные колебания.

Согласно второму правилу Кирхгофа сумма напряжений на резисторе 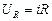и на конденсаторе 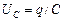равна электродвижущей силе, в данном случае ЭДС самоиндукции, возникающей в катушке при протекании в ней изменяющегося тока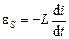

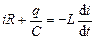. (4.1)

Учитывая, что 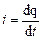, и, следовательно, 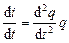, представим выражение (4.1) в виде:

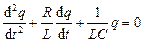. (4.2)

Введем обозначения: , .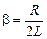

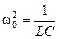Тогда уравнение (4.2) примет вид:

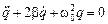. (4.3)

Полученное выражение является дифференциальным уравнением, описывающим процессы в колебательном контуре.

В идеальном случае, когда сопротивлением резистора можно пренебречь, свободные колебания в контуре являются гармоническими.

В этом случае дифференциальное уравнение (4.3) примет вид:

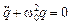, (4.4)

а его решение будет являться гармонической функцией

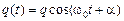, (4.5)

где 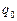– амплитуда колебаний заряда конденсатора; 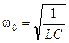– собственная частота колебаний; 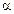– начальная фаза.

Используя выражение для собственной частоты, легко получить формулу Томсона для периода колебаний:

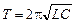. (4.6)

Подстановка (4.5) в уравнение (4.4) показывает, что напряжение на конденсаторе изменяется в одной фазе с изменением заряда:

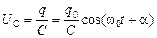. (4.7)

Для силы тока можно получить выражение

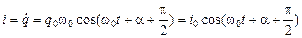. (4.8)

Из формулы (4.8) следует, что колебания силы тока опережают по фазе колебания заряда на 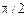. Такой же сдвиг фаз наблюдается для энергий электрического и магнитного полей. Используя выражение для энергии электрического поля заряженного конденсатора 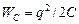и энергии магнитного поля 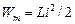и законы колебаний заряда (4.5) и тока (4.8), легко показать, что полная энергия колебательного контура с течением времени не изменяется, т. е. выполняется закон сохранения энергии.