Динамические усилия в цепных тяговых органах.

При расчете и проектировании приводов с цепным тяговым органом определяют динамические усилия в цепи, возбуждаемые приводной звездочкой, а также динамические усилия, возникающие в цепи в пусковой период.

В случае стопорения цепи определяют в ней динамические усилия, которые, как правило, достигают больших значений и часто вызывают разрыв ее.

Для выбора цепей необходимо знать максимальное тяговое усилие в период установившегося движения.

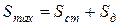, (7.1)

где 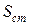- статическое усилие;

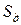- динамическое усилие, возбуждаемое приводной звездочкой.

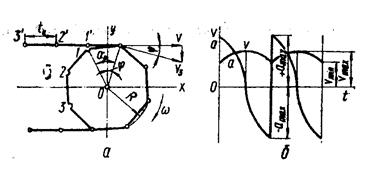
а - зацепление цепи со звездочкой; б - график скорости и ускорения

Рисунок 7.1 - Схемы к расчету скорости и ускорения цепи

Как известно, особенностью цепных передач является то, что цепь движется неравномерно, так как мгновенный радиус набегания цепи на ведущую звездочку изменяется от R до 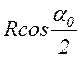, где a₀ – центральный угол звездочки, соответствующий шагу цепи t_ц. При постоянной скорости вращения звездочки скорость зуба по начальной окружности V₃ = const, а скорость цепи (рис.7.1.а,б) будет изменяться по закону

V=V₃cosj=wRcosj, (7.2)

где j = w t – угловое перемещение шарнира, рад;

w - угловая скорость шарнира, рад/с;

R - радиус звездочки по начальной окружности, м;

t - текущее значение времени движения шарнира цепи, с.

Предложим, что цепь во время движения параллельна сама себе. Тогда ускорение цепи

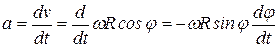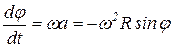
, при (7.3)

Так как угол j изменяется от 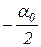до, 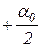то максимальное ускорение изменяется от 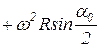до 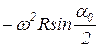(рис.7.1.б).

Подставив в выражение (7.3) 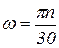, , 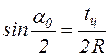,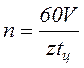получим

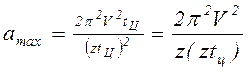м/с², (7.4)

где n – частота вращения звездочки, мин^-1;

t_ц – шаг цепи, м;

z – число зубьев звездочки.

Из формулы (7.4) видно, что ускорение, а следовательно, и динамическое усилие в цепи прямо пропорциональны квадрату скорости ее движения и обратно пропорциональны числу зубьев и диаметру (или периметру) звездочки.

Так как ускорение мгновенно изменяется от – a_max до + a_max, то инерционная сила от ускорения равна 2m a_max , где m – приведенная масса движущихся частей конвейера и груза. Поскольку сила прикладывается мгновенно, производя удар, то динамическая нагрузка на цепь составит 4m a_max. Если учесть инерционную силу, направленную в сторону движения в тот момент, когда цепь движется с замедлением (- a_max), то расчетная динамическая нагрузка на цепь составит

S_д = 4m a_max – m a_max = 3m a_max, (7.5)

Приведенная масса для цепного конвейера

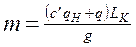, (7.6)

где с’ – коэффициент, учитывающий уменьшение приведенной массы движущихся частей конвейера,

c’ = 2 при L_к < 25 м;

c’ = 1,5 при L_к = 25…60 м;

c’ = 1,0 при L_к > 60 м;

g – ускорение силы тяжести, м/с²;

q и q_н – погонные нагрузки от транспортируемого груза и движущегося органа машины, Н/м.

Подставив в формулу (7.5) значения a_max и m, получим

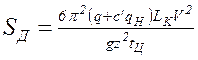. (7.7)

Формула (7.7) получена при условии, что тяговая цепь является абсолютно твердым телом. Динамические усилия, определенные по формуле (7.7), в цепях коротких приводов незначительно отличаются от действительных. Введение коэффициента c’ дало возможность приспособить формулу (7.7) для определения динамических усилий в цепях длинных приводов и широко использовать в инженерных расчетах. В действительности в тяговых цепях, обладающих упругостью и приводимых в движение звездочками, возникают динамические усилия колебательного характера.

Установлено, что в тяговых цепях возникает сложный колебательный процесс, зависящий от параметров и характеристик цепей, звездочек, скорости движения, величины движущихся масс, конструкции рабочего органа цепного привода, размеров и формы трассы и др. Доказано, динамические усилия в цепях возрастают при приближении частоты вынужденных колебаний цепи к собственной частоте, а при работе на резонансной частоте динамические усилия становятся максимальными.

Однако до настоящего времени не разработан инженерный метод определения динамических усилий в цепях различных приводов.

Более точное решение задачи по определению динамических усилий в цепях возможно при условии, когда тяговая цепь рассматривается как односторонняя упругая связь.

Таким образом, предварительно натянутую цепь можно представить в виде упругого стержня, один конец которого получает продольные силовые импульсы от приводной звездочки. Периодически прикладываемые импульсы вызывают в упругом стержне вынужденные продольные колебания, а периодическое изменение знака ускорения конца упругого стержня приводит к возникновению в нем собственных колебаний.

Скорости распространения упругой волны вдоль тягового органа соответственно в рабочей и холостой ветвях:

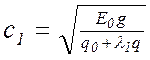; (7.8)

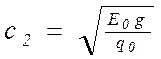, (7.9)

где Е₀ – статическая жесткость цепи, кгс;

g – ускорение силы тяжести, м/с²;

q₀ и q – погонный вес цепи и транспортируемого груза , Н/м;

l₁ – коэффициент участия массы перемещаемого груза в неравномерном движении цепи; для скребковых конвейеров l₁ @ 0,4.

Если груз перемещается в сосудах (ковшовые элеваторы) или на пластинчатом полотне, то принимают l₁ = 1.

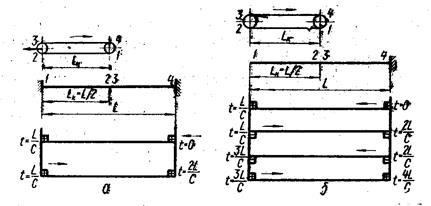
а - первоначальное натяжение больше критического;

б - первоначальное натяжение меньше критического.

Рисунок 7.2 - Модели из упругих стержней цепного привода для одной цепи

и схемы распространения упругих деформаций в цепях.

Так как скорости распространения упругих волн в рабочей и холостой ветвях различны, то эквивалентная схема тягового органа может быть представлена составным упругим стержнем, колебательное движение которого описывается системой двух волновых уравнений:

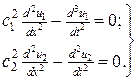(7.10)

где u₁ и u₂ – функции упругого смещения набегающей и сбегающей ветвей.

Для решения этих уравнений приняты следующие граничные условия:

1) первоначальное натяжение цепи больше критического (под критическим понимается такое первоначальное натяжение, при котором статическое натяжение в сумме с динамическим (рис. 7.2. а) не падает до нуля ни в одной из точек тягового органа);

2) первоначальное натяжение меньше критического, т.е. в месте сбегания со звездочки цепь провисает (рис. 7.2. б).

В первом случае представим, что концы упругого стержня жестко заделаны (рис. 7.2.а).

Приложим в точку 4 продольный импульс. Тогда период основного тона собственных колебаний цепи равен времени двукратного пробега упругой волны по ее контуру, т. е.

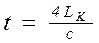, (7.11)

где L_к – длина конвейера, м;

с – средняя скорость распространения упругой волны, м/с,

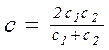. (7.12)

Во втором случае представим, что один конец упругого стержня жестко закреплен, а второй – свободный (рис. 1.2. б). В этом случае период основного тона собственных колебаний равен времени четырехкратного пробега упругой волны по контуру цепи, т. е.

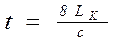(7.13)

Период возмущающей силы (время поворота звездочки на одну грань)

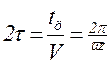, (7.14)

где V – скорость движения цепи, м/с;

w - угловая скорость вращения звездочки, рад/с;

z - число граней звездочки.

При совпадении периода собственных колебаний и периода возмущающей силы наступает резонанс, т. е. при 2t = t.

Если натяжение цепи больше критического, то резонанс наступает при

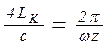, (7.15)

а если натяжение меньше критического, то при

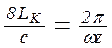. (7.16)

Для одноприводных конвейеров из формул (7.15) и (7.16) находят резонирующие длины ( 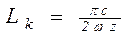и 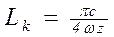) и резонансные скорости при натяжении больше критического

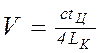, (7.17)

при натяжении меньше критического

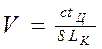. (7.18)

Максимальная нагрузка в цепном тяговом органе равна сумме статических и динамических нагрузок, а минимальная – их разности.

Максимальную динамическую нагрузку на цепь определяют по формуле

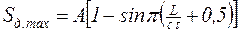, (7.19)

где А – амплитуда колебаний усилия, кгс;

t - полупериод возмущающей силы (формула 7.14);

L - длина тяговой цепи, м.

Нагрузка S_{д. max} (7.19) становится равной нулю при L = 0; 4сt и 2А при

L= сt; 3сt; 5сt.

Таким образом, явление резонанса возникает тогда, когда отношение периода собственных колебаний цепи к периоду возмущающей силы 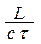будет нечетным числом, а если 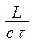будет четным числом, то колебания будут совершаться в противофазе.

Амплитуда А может быть выражена половиной величины динамических нагрузок при резонансе, т. е.

А= 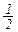(j₄-j₂) 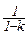, (7.20)

где (j₄ - j₂ )– разность значений исходных составляющих. Величина которой зависит от полупериода возмущающей силы t, усредненного коэффициента f и жесткости цепи Е_0; для вычисления значения (j₄ - j₂)построена номограмма (рис.3);

k – коэффициент затухания собственных колебаний,

k=k₁k₂, (7.21)

k₁ = 0,65 … 0,68 – коэффициент отражения;

k₂ – коэффициент прохождения,

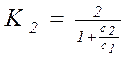. (7.22)

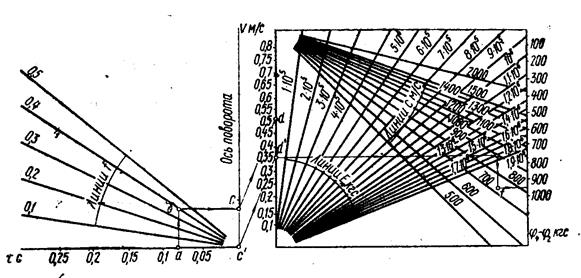
Рисунок 7. 3 - Номограмма для вычисления функции (φ₄ - φ₂)

Усредненный коэффициент сопротивления

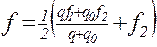, (7.23)

где f₁ – коэффициент сопротивления движению материала по желобу;

f₂ – коэффициент сопротивления движению скребковой цепи по желобу.

Динамическое усилие в цепи при пуске конвейера вычисляют приближенно по формуле

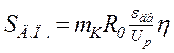, (7.24)

где m_к – приведенная масса движущихся частей конвейера и груза,

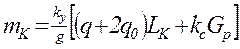, (7.25)

k_y = 0,85…0,95 – коэффициент, учитывающий упругое удлинение цепей;

k_c = 0,5…0,7 – коэффициент, учитывающий, что окружная скорость части вращающихся масс меньше, чем V;

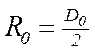- радиус делительной окружности звездочки;

e_дв – угловое ускорение вала двигателя;

h - к. п. д. привода;

U_p – передаточное число привода.