Закон Архимеда. Плавание тел
5.1. Основные положения
Основным законом теории плавания тел является закон Архимеда: Сила давления покоящейся жидкости на погруженное в нее тело равна весу жидкости в объеме, вытесненном телом, направлена по вертикали вверх и приложена в центре тяжести этого объема.
Рис. 5.1
Достаточно просто обосновать закон Архимеда экспериментально. Плавание тела легко наблюдать. Не сложно экспериментально определить и значение силы, выталкивающей плавающее тело из жидкости. Для тел простой геометрической формы легко установить и линию действия равнодействующей сил избыточного давления (рис. 5.1).
Избыточное давление, создаваемое столбом жидкости в каждой точке боковой поверхности цилиндрического тела определяется как функция угла 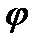
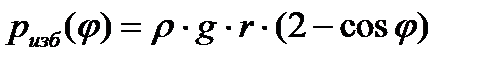 . . | (5.1) |
В силу симметричности действующей нагрузки относительно оси  , равнодействующая сил давления
, равнодействующая сил давления  направлена по оси
направлена по оси 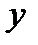 вверх и имеет модуль
вверх и имеет модуль
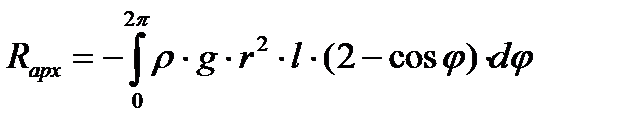 . . | (5.2) |
Вычисление интеграла (5.2) дает результат
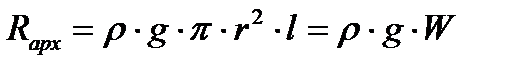 , , | (5.3) |
где 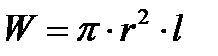 - объем жидкости, вытесненной плавающим телом.
- объем жидкости, вытесненной плавающим телом.
Полученный результат справедлив и для тела с произвольной формой внешней поверхности и называется законом Архимеда
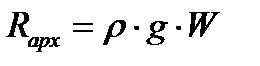 . . | (5.4) |
В зависимости от соотношения силы тяжести тела 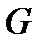 и выталкивающей силы
и выталкивающей силы 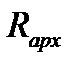 возможны три случая:
возможны три случая:
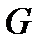 >
> 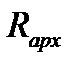 - тело тонет;
- тело тонет;
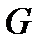 <
< 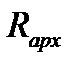 - тело всплывает;
- тело всплывает;
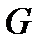 =
= 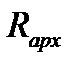 - тело плавает.
- тело плавает.
В состоянии плавания положение тела может измениться в результате приложения внешних возмущающих сил, которые выводят его из положения статического равновесия. Способность тела восстанавливать исходное положение после прекращения действия возмущающих сил называют остойчивостью. Условия остойчивости при подводном плавании (когда тело полностью погружено в жидкость) и надводном плавании (тело частично погружено в жидкость) различны.
При подводном плавании (рис. 5.2а) остойчивость имеет место, если центр тяжести тела 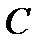 располагается ниже центра водоизмещения
располагается ниже центра водоизмещения 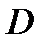 . В этом случае пара, образованная силой тяжести и архимедовой силами стремится повернуть тело в сторону уменьшения возникшего крена. Если точка
. В этом случае пара, образованная силой тяжести и архимедовой силами стремится повернуть тело в сторону уменьшения возникшего крена. Если точка 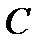 располагается выше точки
располагается выше точки 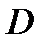 , пара (
, пара ( 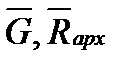 ) будет способствовать увеличению крена, вызванного возмущающими силами (рис. 5.2б), и тело потеряет остойчивость.
) будет способствовать увеличению крена, вызванного возмущающими силами (рис. 5.2б), и тело потеряет остойчивость.
Рис. 5.2
При надводном плавании тело остойчиво при расположении центра тяжести 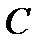 ниже центра давления
ниже центра давления 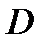 (рис.5.3а), когда пара (
(рис.5.3а), когда пара ( 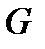 ,
, 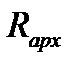 ) с плечом
) с плечом 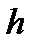 стремится уменьшить угол крена
стремится уменьшить угол крена 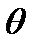 , появившийся в результате действия внешних возмущений. Ярким примером высокой остойчивости служит плавание яхты.
, появившийся в результате действия внешних возмущений. Ярким примером высокой остойчивости служит плавание яхты.
| а) б) в) |
Рис.5.3
Следует обратить внимание на то, что при надводном плавании центр давления не остается в плоскости продольной симметрии тела, а смещается из положения 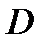 в новое положение – точку
в новое положение – точку 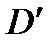 . Точку пересечения линии действия архимедовой силы с плоскостью продольной симметрии тела называют метацентром (на рис. 5.3 точка М).
. Точку пересечения линии действия архимедовой силы с плоскостью продольной симметрии тела называют метацентром (на рис. 5.3 точка М).
Остойчивость при надводном плавании будет сохраняться и в том случае, если центр тяжести располагается выше центра давления, но только при условии, что он находится ниже метацентра М (рис. 5.3 в). Если же центр тяжести располагается выше центра давления и метацентра, то пара ( 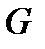 ,
, 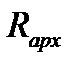 ) стремится увеличить угол крена
) стремится увеличить угол крена 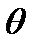 . Плавающее тело в этом случае не обладает статической остойчивостью (рис. 5.3б).
. Плавающее тело в этом случае не обладает статической остойчивостью (рис. 5.3б).
Примеры решения задач
Пример 5.1
Плавучий железобетонный тоннель с наружным диаметром D =10 м и толщиной стенок 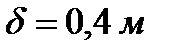 удерживается от всплытия тросами, расположенными попарно через каждые
удерживается от всплытия тросами, расположенными попарно через каждые 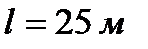 длины тоннеля. Определить натяжение тросов, если вес 1м дополнительной нагрузки от дорожного покрытия составляет q=9,8 кН/м, удельный вес бетона
длины тоннеля. Определить натяжение тросов, если вес 1м дополнительной нагрузки от дорожного покрытия составляет q=9,8 кН/м, удельный вес бетона 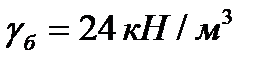 и угол
и угол 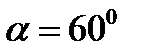
Рис. 5.4
Решение
На участок тоннеля длиной 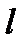 действуют:
действуют:
· сила тяжести 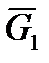 участка железобетонной трубы;
участка железобетонной трубы;
· сила тяжести 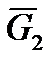 дорожного покрытия;
дорожного покрытия;
· архимедова сила 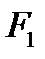 , выталкивающая тоннель вверх;
, выталкивающая тоннель вверх;
· силы натяжения тросов 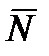 , удерживающие тоннель в затопленном состоянии.
, удерживающие тоннель в затопленном состоянии.
Вес участка тоннеля длиной l= 25 м с дополнительной нагрузкой 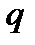 равен
равен
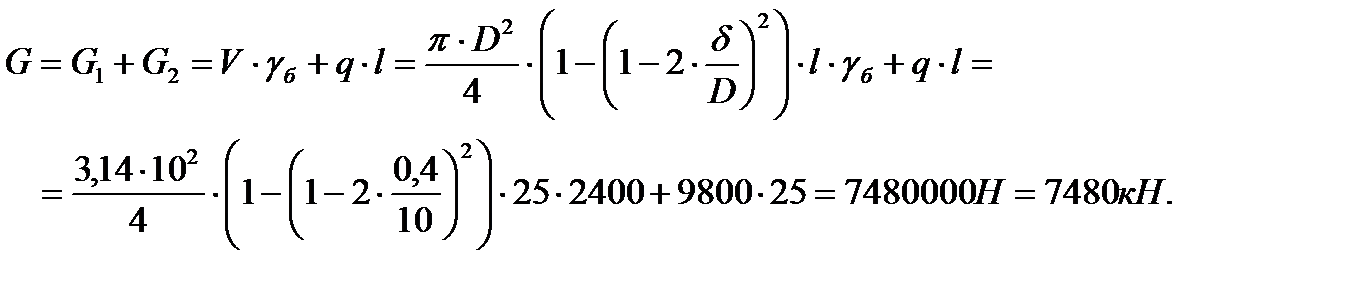 | (5.1) |
Выталкивающая сила равна весу воды в объеме, вытесняемом 25 метрами тоннеля
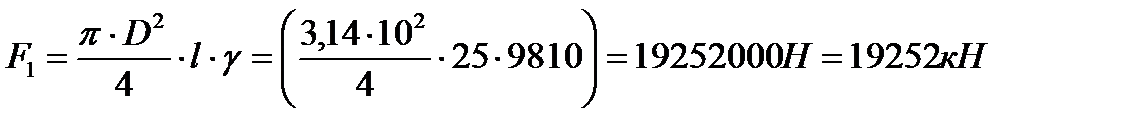 . . | (5.2) |
Из условия равновесия сил, действующих на участок тоннеля
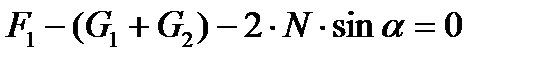 , , |
находим
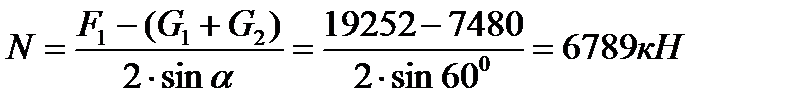 , , | (5.3) |
Пример 5.2
Нефтеналивной танкер, груженный моторным топливом удельного веса 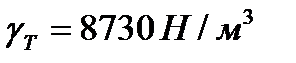 , перекачал в рейдовую баржу
, перекачал в рейдовую баржу 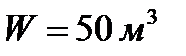 топлива. Осадка танкера (глубина его погружения в воду) уменьшилась при этом на H = 0,1 м . Определить площадь сечения танкера по ватерлинии.
топлива. Осадка танкера (глубина его погружения в воду) уменьшилась при этом на H = 0,1 м . Определить площадь сечения танкера по ватерлинии.
Рис. 5.5
Решение
На плавающее тело действуют сила тяжести 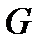 и выталкивающая сила воды
и выталкивающая сила воды 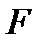 . При сливе
. При сливе 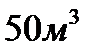 топлива вес танкера уменьшается на величину
топлива вес танкера уменьшается на величину
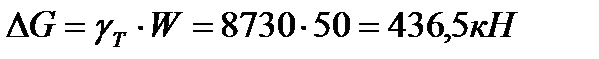 | (5.4) |
На такую же величину уменьшится и выталкивающая сила за счет всплытия корпуса на 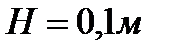 . Считая площадь сечения корпуса в окрестности ватерлинии постоянной, можно записать
. Считая площадь сечения корпуса в окрестности ватерлинии постоянной, можно записать
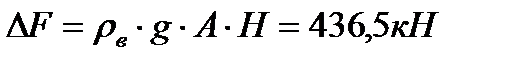 . . | (5.5) |
Из последнего равенства и находим площадь сечения танкера по ватерлинии
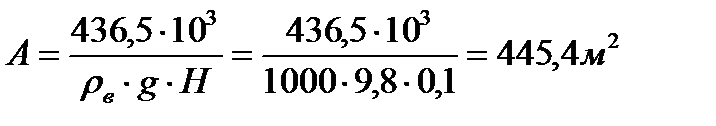 . . | (5.6) |
Пример 5.3
Давление p воды в водопроводной трубе диаметра d стремится открыть клапан k . Клапан при горизонтальном положении рычага ab закрывает отверстие трубы. Полагая стержень abc и полый шар диаметра D невесомыми, определить соотношение между плечами a и b рычага, обеспечивающее плотное закрытие клапана. Известно, что 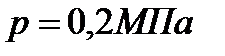 ,
, 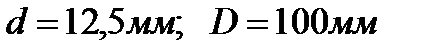
Рис. 5.6
Решение
Рычаг 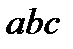 запорного устройства, закрепленный в шарнире
запорного устройства, закрепленный в шарнире  , находится в равновесии под действием силы давления воды на клапан
, находится в равновесии под действием силы давления воды на клапан  и силы, выталкивающей поплавок
и силы, выталкивающей поплавок 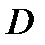 из воды
из воды 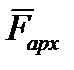 . Величина этих сил
. Величина этих сил
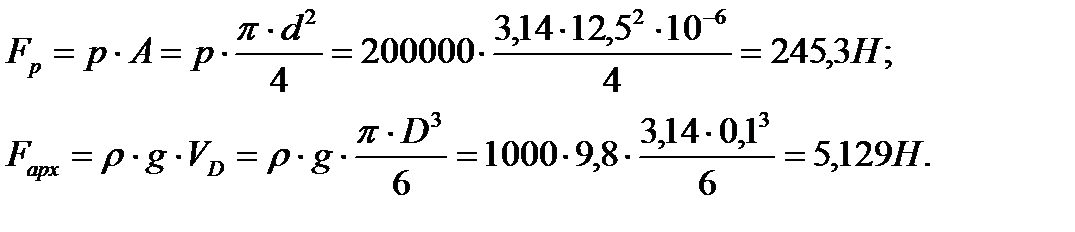 | (5.7) |
Из условия равновесия рычага 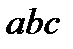
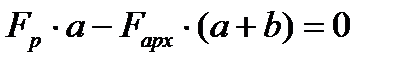 | (5.8) |
находим
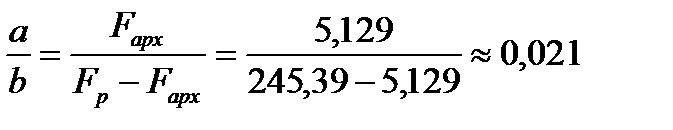 | (5.9) |
Пример 5.4
Резервуар водонапорной башни оборудован ограничителем уровня воды, представляющим собой клапан 1, соединенный тягой с поплавком 2.
Определить расстояние h от дна резервуара до нижней плоскости поплавка, при котором будет обеспечена глубина воды в резервуаре H = 4,5 м . Диаметр поплавка D = 0,4 м , вес поплавка с тягой и клапаном 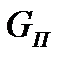 =120 H , диаметр клапана d = 0,1 м .
=120 H , диаметр клапана d = 0,1 м .
Рис. 5.7
Решение
При уровне воды H менее 4,5м клапан закрыт. При повышении уровня более 4,5м погружение поплавка в воду достигает такой величины, при которой выталкивающая сила воды 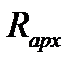 превышает силу тяжести поплавка
превышает силу тяжести поплавка 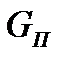 и равнодействующую гидростатического давления воды
и равнодействующую гидростатического давления воды 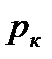 , действующую на клапан. Клапан открывается и через него сбрасывается часть воды.
, действующую на клапан. Клапан открывается и через него сбрасывается часть воды.
Сила давления воды на клапан
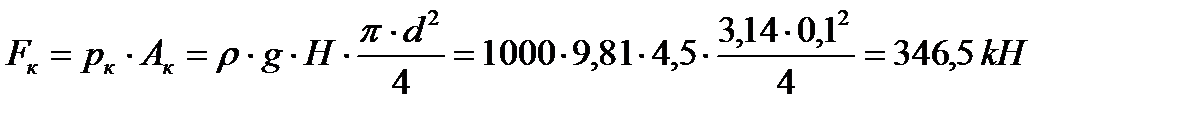 | (5.10) |
Выталкивающая сила 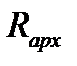 равна весу воды, в объеме подводной части поплавка
равна весу воды, в объеме подводной части поплавка
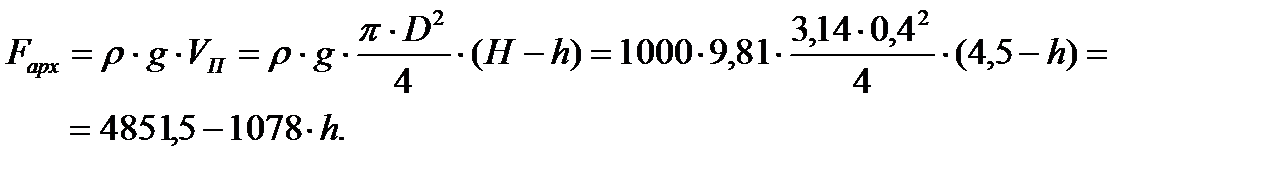 | (5.11) |
Из условия равновесия сил, действующих на поплавок
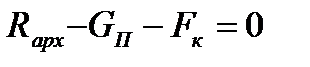 , , | (5.12) |
находим
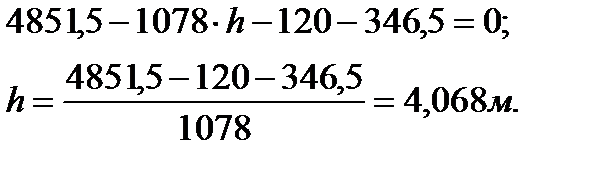 | (5.13) |
Пример 5.5
Определить количество бревен 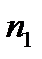 , из которых нужно сколотить плот, чтобы перевезти груз весом
, из которых нужно сколотить плот, чтобы перевезти груз весом 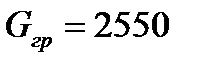 H . Диаметр бревен d =16см, их длина L = 7 м. Осадка плота H равномерная и составляет 0,13 м. Массу перевозчика принять m = 75 кг, а относительную плотность намокших бревен δ=0,75. Какое количество бревен
H . Диаметр бревен d =16см, их длина L = 7 м. Осадка плота H равномерная и составляет 0,13 м. Массу перевозчика принять m = 75 кг, а относительную плотность намокших бревен δ=0,75. Какое количество бревен 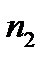 понадобится для решения той же задачи, если их верх (верх плота) будет заподлицо со свободной поверхностью воды?
понадобится для решения той же задачи, если их верх (верх плота) будет заподлицо со свободной поверхностью воды?
Рис. 5.8
Решение
Плавание плота возможно, если сумма сил тяжести плота, груза и перевозчика 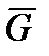 , будет уравновешена выталкивающей силой
, будет уравновешена выталкивающей силой 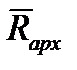
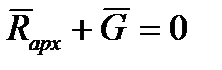 | (5.14) |
При осадке плота на величину 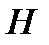 выталкивающая сила
выталкивающая сила 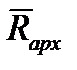 будет равна весу воды в объеме, ограниченном затопленной площадью поперечного сечения
будет равна весу воды в объеме, ограниченном затопленной площадью поперечного сечения  при длине бревна
при длине бревна 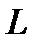 , с учетом количества бревен
, с учетом количества бревен
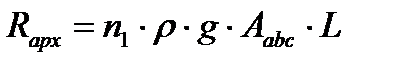 , , | (5.15) |
здесь
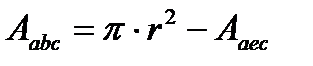 . . | (5.16) |
Немного геометрии
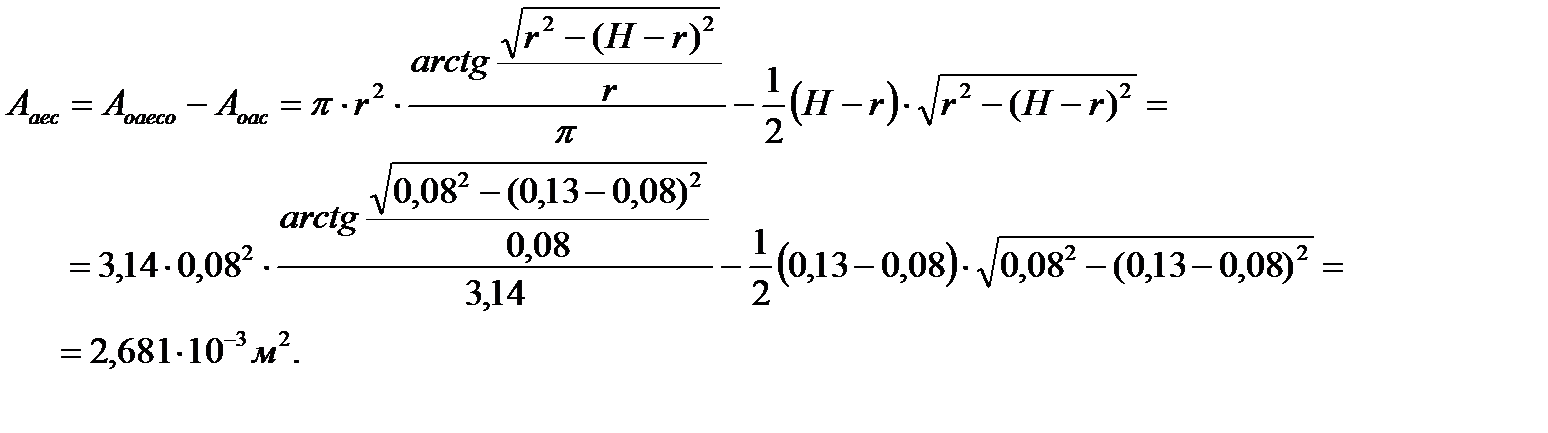 | (5.17) |
Тогда
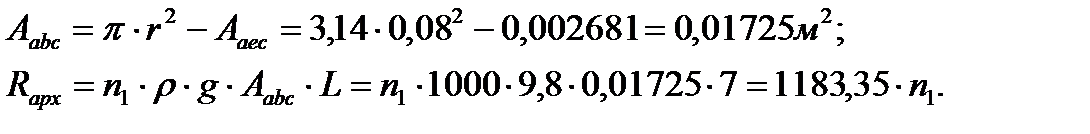 . . | (5.18) |
Теперь из условия уравновешенности найдем необходимое число бревен для плота
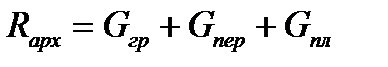 , , | (5.19) |
где
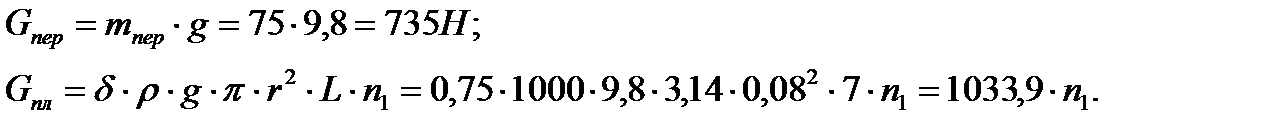 , , |
Теперь находим необходимое число бревен в составе плота
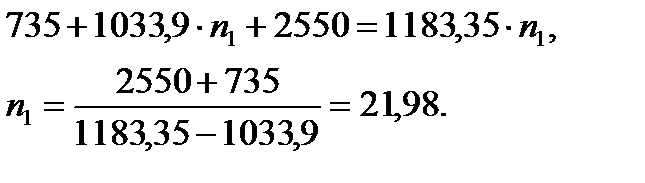 , , | (5.20) |
Следует принять 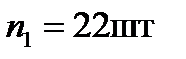 при осадке
при осадке 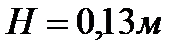 .
.
При H=d выталкивающая сила плота из 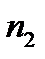 бревен
бревен
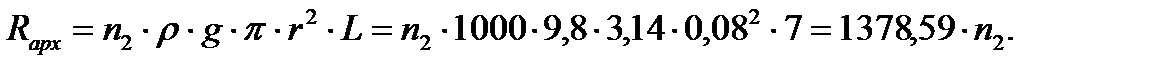 | (5.21) |
В этом случае количество бревен в конструкции плота должно быть равно
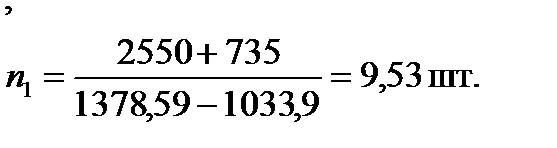 , , | (5.22) |
Необходимо принять при осадке 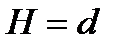 число бревен в конструкции плота
число бревен в конструкции плота 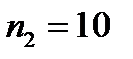 шт.
шт.
6. Равновесие жидкости в движущемся сосуде
Эти задачи представляют интерес при определении нагрузок на стенки сосуда, движущегося поступательно и прямолинейно или вращающегося с постоянной угловой скоростью, когда модуль ускорения каждой частицы жидкости не изменяется по величине. Использование принципа Д’Аламбера позволяет свести эти задачи к задаче равновесия жидкости в движущемся сосуде и использовать для их решения основное уравнение гидростатики.
6.1. Равновесие жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси
При равновесии жидкости в сосуде, равномерно вращающемся относительно вертикальной оси, поле массовых сил неоднородно. Поверхности уровня представляют параболоиды вращения, ось которых совпадает с осью вращения сосуда.
Рис. 6.1
Уравнение поверхности постоянного давления в подвижных координатах 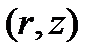 (в частности, свободной поверхности жидкости), имеет вид
(в частности, свободной поверхности жидкости), имеет вид
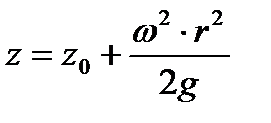 . . | (6.1) |
Высота параболоида свободной поверхности определяется по формуле
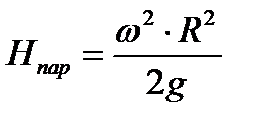 . . | (6.2) |
Давление в произвольной точке вращающейся жидкости определяется уравнением
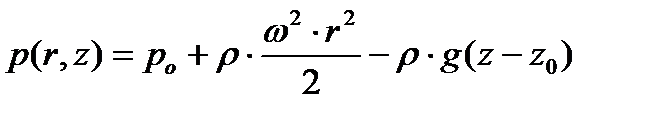 , , | (6.3) |
где
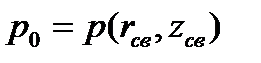 – давление в точках параболоида свободной поверхности, координаты вершины которого
– давление в точках параболоида свободной поверхности, координаты вершины которого 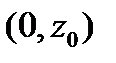 .
.
По вертикали давление определяется глубиной расположения точки под параболоидом свободной поверхности 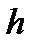 , т.е. давление распределяется по гидростатическому закону
, т.е. давление распределяется по гидростатическому закону
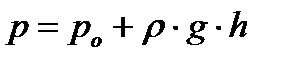 . . | (6.4) |
Значение координаты 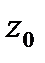 находят, как правило, из условия равенства объемов жидкости в состоянии покоя и при равномерном вращении
находят, как правило, из условия равенства объемов жидкости в состоянии покоя и при равномерном вращении
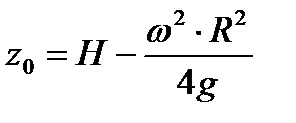 . . | (6.5) |
Уравнение свободной поверхности вращающейся жидкости легко получить из уравнения (6.3) при условии, что 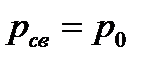 ,
, 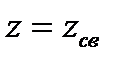
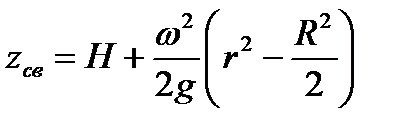 . . | (6.6) |
6.2. Примеры решения задач
Пример 6.1
Открытый цилиндрический сосуд диаметром D = 0,04 м и высотой Н = 0,1 м наполнен до половины водой. С каким предельным числом оборотов 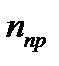 можно вращать этот сосуд относительно его геометрической вертикальной оси, чтобы из него не выливалась вода?
можно вращать этот сосуд относительно его геометрической вертикальной оси, чтобы из него не выливалась вода?
Рис. 6.2
Решение
Свободная поверхность жидкости, вращающейся с угловой скоростью 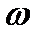 , имеет форму параболоида вращения и описывается уравнением (6.6), необходимо только учесть, что в покое высота слоя воды по условию задачи равна
, имеет форму параболоида вращения и описывается уравнением (6.6), необходимо только учесть, что в покое высота слоя воды по условию задачи равна 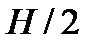
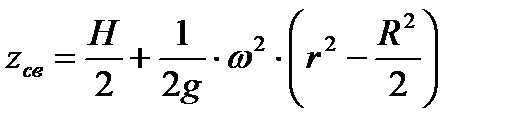 . . | (6.7) |
При максимальной угловой скорости 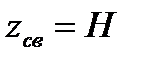 ,
, 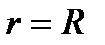 . Тогда
. Тогда
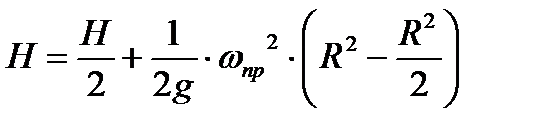 . . | (6.8) |
Откуда находим
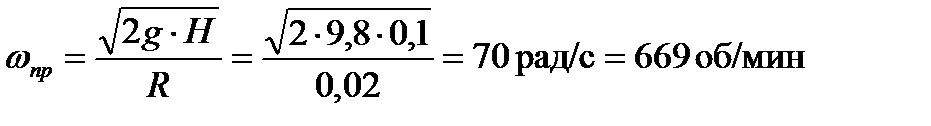 . . | (6.9) |
Пример 6.2
Закрытая цилиндрическая коробка высотой H и диаметром 2R наполнена жидкостью на 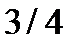 высоты. С какой угловой скоростью
высоты. С какой угловой скоростью 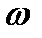 должна вращаться коробка около ее вертикальной оси, чтобы параболоид вращения коснулся дна свободной поверхности?
должна вращаться коробка около ее вертикальной оси, чтобы параболоид вращения коснулся дна свободной поверхности?
Рис. 6.2
Решение
Вершина свободной поверхности жидкости во вращающемся сосуде имеет координату 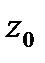 , которая определяется по формуле (6.5). Принимая во внимание, что в состоянии покоя уровень жидкости в сосуде равен
, которая определяется по формуле (6.5). Принимая во внимание, что в состоянии покоя уровень жидкости в сосуде равен 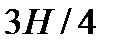 , запишем
, запишем
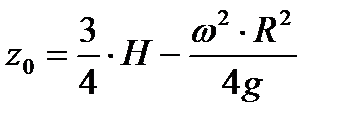 . . | (6.10) |
При касании вершины свободной поверхности дна сосуда 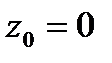 . Угловая скорость вращения в этот момент равна
. Угловая скорость вращения в этот момент равна
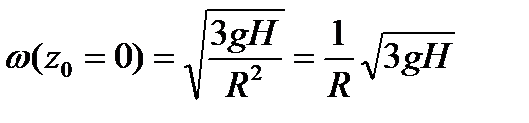 . . | (6.11) |
Высота параболоида свободной поверхности при такой скорости вращения определяется по формуле (6.2)
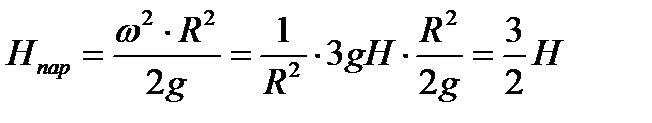 . . | (6.12) |
Пример 6.3
Вертикальный открытый сверху цилиндрический сосуд радиуса R и высотой H равномерно вращается вокруг вертикальной оси. делая n оборотов в минуту. Какой объем жидкости будет удерживаться в этом сосуде?
Рис. 6.3
Решение
Максимальный объем жидкости, удерживаемый в сосуде при вращении с угловой скоростью 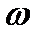 , определяется условием достижения верхней точкой свободной поверхности жидкости верхнего края боковой стенки. Формально это условие можно записать так (см. (6.2), (6.5))
, определяется условием достижения верхней точкой свободной поверхности жидкости верхнего края боковой стенки. Формально это условие можно записать так (см. (6.2), (6.5))
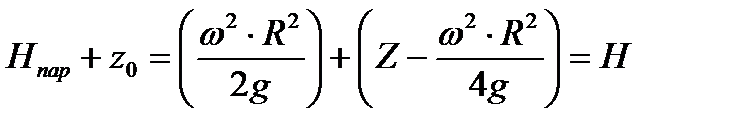 , , | (6.13) |
где 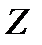 - высота жидкости в неподвижном сосуде
- высота жидкости в неподвижном сосуде
Решение уравнения (6.13) относительно 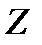 дает следующий результат
дает следующий результат
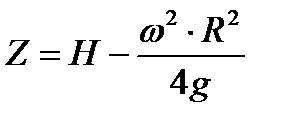 . . | (6.14) |
Объем жидкости, находящейся в сосуде при угловой скорости вращения 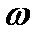 равен
равен
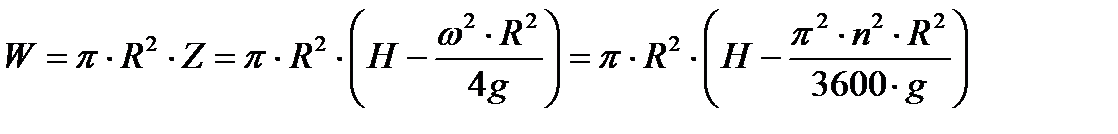 . . | (6.15) |
Пример 6.4
Отливка чугунных полых цилиндров производится в форму, вращающуюся вокруг вертикальной оси. Отливка вращается, делая 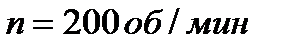 ; высота отливки H = 0,25 м; максимальный внутренний диаметр
; высота отливки H = 0,25 м; максимальный внутренний диаметр 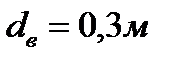 . Насколько толщина стенки цилиндра в нижней части будет больше, чем в верхней?
. Насколько толщина стенки цилиндра в нижней части будет больше, чем в верхней?
Найти число оборотов в минуту 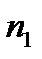 , которое следует сообщить форме, чтобы разница в толщине стенки
, которое следует сообщить форме, чтобы разница в толщине стенки 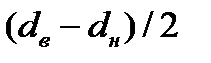 была не более 0,01м.
была не более 0,01м.
Рис. 6.4
Решение
Внутренняя поверхность отливки во вращающейся форме представляет параболоид вращения. Различие в толщине стенки у нижнего торца (сечение 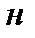 ) и верхнего торца (сечение
) и верхнего торца (сечение 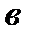 ) отливки определяется разностью координат
) отливки определяется разностью координат 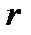 точек свободной поверхности
точек свободной поверхности
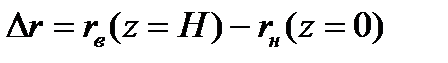 . . | (6.16) |
Используя уравнение свободной поверхности (6.1), находим
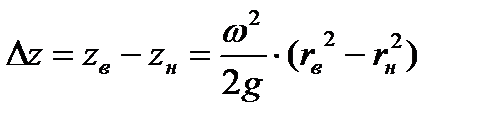 . . | (6.17) |
Далее после очевидных преобразований получаем
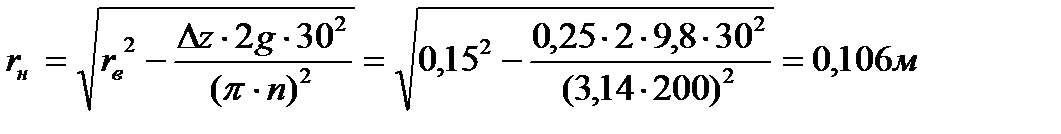 , , | (6.18) |
что дает возможность определить разность в толщине стенок
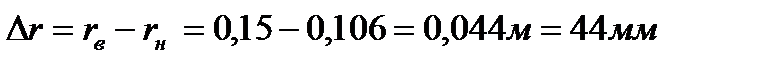 . . | (6.19) |
Для определения угловой скорости, при которой разность в толщине стенки не превысит 0,01м, имеем условие
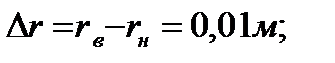 . . | (6.20) |
При 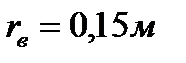
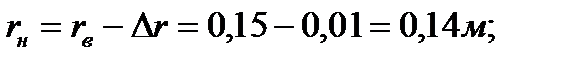 . . | (6.21) |
Тогда из формулы (6.17) следует
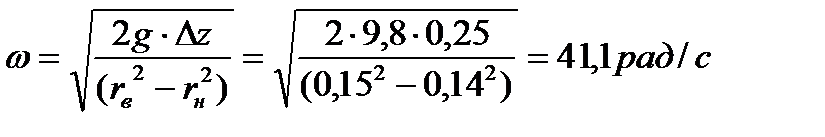 . . | (6.22) |
Число оборотов в минуту, обеспечивающее разность толщин стенки в верхней и нижней части цилиндра 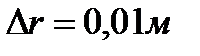 , равно
, равно
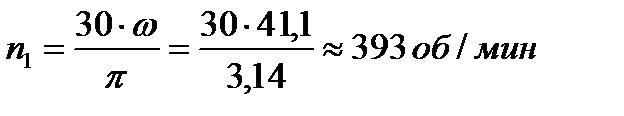 . . | (6.23) |
Пример 6.5
| Рис. 6.5 | Открытый цилиндрический сосуд наполнен водой и вращается с постоянной угловой скоростью 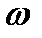 . В результате вращения вода поднялась над дном сосуда на высоту H = 2 м. Определить манометрическое давление p на дне сосуда в центре и через каждые 20 см от его оси до стенки, а также расстояние . В результате вращения вода поднялась над дном сосуда на высоту H = 2 м. Определить манометрическое давление p на дне сосуда в центре и через каждые 20 см от его оси до стенки, а также расстояние 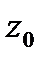 от дна сосуда до вершины параболоида (точка А). Диаметр сосуда D =1,2 м, число оборотов сосуда от дна сосуда до вершины параболоида (точка А). Диаметр сосуда D =1,2 м, число оборотов сосуда  . . |
Решение
Манометрическое давление в произвольной точке дна сосуда можно определить, используя формулу (6.3)
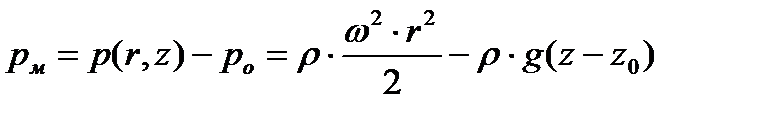 , , | (6.24) |
что при 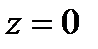 дает расчетную формулу
дает расчетную формулу
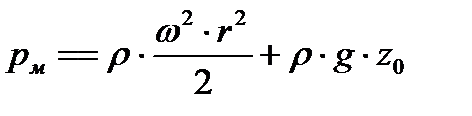 . . | (6.25) |
Так как 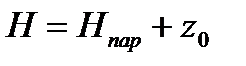 , то, применяя формулу (6.2), находим
, то, применяя формулу (6.2), находим
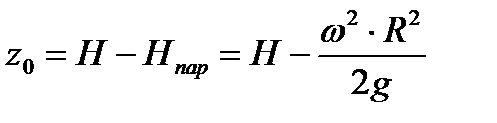 . . | (6.26) |
Подставляя (6.26) в (6.25), получаем
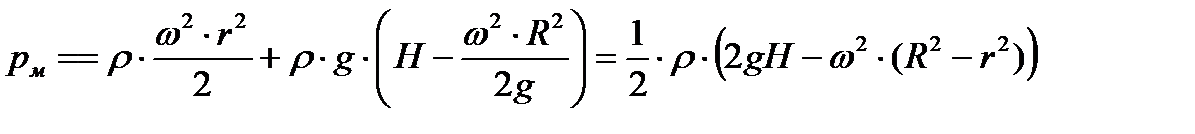 . . | (6.27) |
Расчет по формуле (6.27) дает следующие результаты
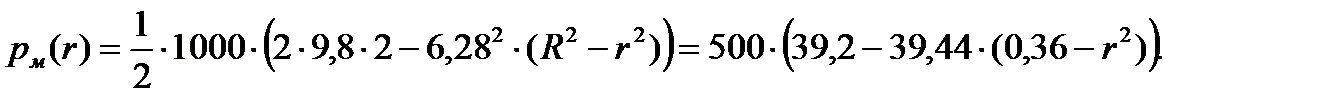 | |
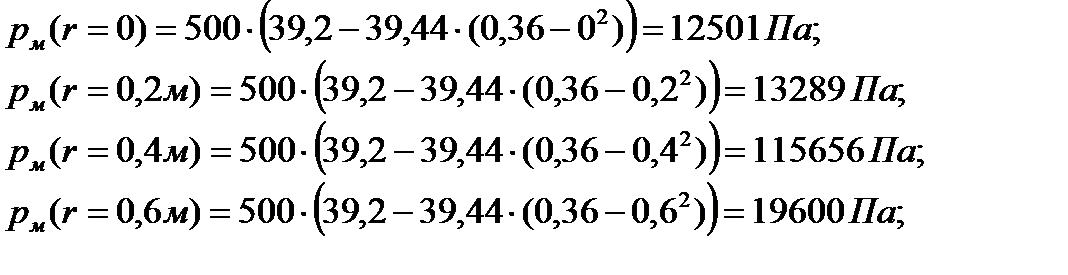 | (6.28) |
Графически результаты расчета представлены на рис. 6.5.
Литература
1. Гидравлика и гидропневмопривод (задачник), под ред. проф. Ю.А. Беленкова. М., «ЭКЗАМЕН», 2009 – 286с.
2. Гориславец С.С. Сборник задач с примерами гидравлических расчетов по «Гидростатике», ООО « Издательский дом – Типография купца Тарасова», Пермский край, г. Березники, 2007г., 234 с.
3. Кудинов В.А., Карташов Э.М. Гидравлика. М., «Высшая школа», 2008 -199с.
4. Метревели В.Н.Сборник задач по курсу гидравлики с решениями. М., «Высшая школа», 2008 – 190с.
5. Примеры расчетов по гидравлике, под ред. А.Д.Альтшуля. М., «Стойиздат», 1976 – 255с.
6. Сазанов И.М. Гидравлика (конспект лекций). М., МГТУ «СТАНКИН», 2005 -190с.
7. Шейпак А.А. Гидравлика и гидропривод (учебное пособие, Ч I). Основы механики жидкости и газа. М., МГИУ, 2003 - 192с.
8. Штеренлихт Д.В. Гидравлика. М., КолоС, 2005 - 655с.
Оглавление
| Основные физические свойства жидкости и газа ……………… | |
| Гидростатика ……………………………………. .……………… | |
| Давление жидкости на плоскую стенку ……….. .……………… | |
| Давление жидкости на криволинейную стенку ………………… | |
| Закон Архимеда. Плавание тел …………………..……………… | |
| Равновесие жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси ………………………….……………… | |
| Литература ………………………………………………………… |
