Формулы полной вероятности и бейеса

Если событие А может осуществиться только при наступлении одного из событий 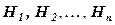которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле полной вероятности

.

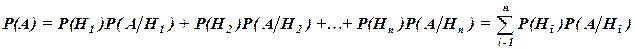Для вычисления вероятности гипотезы 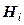в предположении, что событие А произошло, используют формулу Бейеса

.

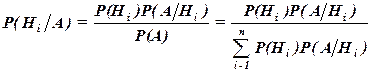5.1. В тире имеется пять винтовок, вероятности попадания из которых равны соответственно 0,5, 0,6, 0,7, 0,8, 0,9. Найти вероятность попадания при одном выстреле, взяв винтовку наугад.

5.2. 30% приборов собирает специалист высокой квалификации и 70% – специалист средней квалификации. Надёжность работы прибора, собранного специалистом высокой квалификации, равна 0,9, собранного специалистом средней квалификации – 0,8. Взятый прибор оказался надёжным. Найти вероятность того, что он собран специалистом высокой квалификации.

5.3. В первом ящике находятся 3 белых и 2 чёрных шара, а во втором ящике – 4 белых и 4 чёрных шара. Из первого ящика переложили во второй 2 случайным образом выбранных шара. Затем из второго ящика достали один шар. Какова вероятность того, что он белый?

5.4. Допустим, что 20% всех людей – флегматики. Пусть 40% всех флегматиков страдают избыточным весом (из остальных людей – 30%). Встретился полный человек. Какова вероятность того, что он флегматик?

5.5. На сборку поступают детали с трёх автоматов. Первый даёт 25% , второй – 30%, третий – 45% всех деталей, поступающих на сборку. Первый автомат допускает 0,1% брака деталей, второй – 0,2%, третий – 0,3%. Найти вероятность поступления на сборку бракованной детали и вероятность того, что оказавшаяся бракованной деталь изготовлена первым станком.

5.6. Из 10 студентов 3 подготовлены отлично (знают все 20 вопросов ), 4 – хорошо (знают 16 вопросов), 2 – посредственно (знают 10 вопросов), 1 – плохо (знает 5 вопросов). Вызванный студент ответил на два заданных ему вопроса. Какова вероятность того, что он был подготовлен отлично?

5.7. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле равна 0,3, при втором – 0,6, при третьем – 0,8. При одном попадании вероятность поражения цели – 0,4, при двух попаданиях – 0,7, при трёх попаданиях – 1,0. Найти вероятность поражения цели при трёх выстрелах.

5.8. В первом ящике находятся 7 белых и 3 чёрных шара, а во втором –
2 белых и 3 чёрных шара. Из первого ящика выбирают случайным образом один шар и перекладывают его во второй ящик. Затем из второго ящика один шар перекладывают в первый ящик. После этой процедуры из первого ящика извлекают один шар. Найти вероятность того, что шар, извлечённый из первого ящика, оказался белым.

5.9. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых автомашин, проезжающих по тому же шоссе, как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1, для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

5.10. Вероятность изготовления стандартной детали равна 96%. Упрощённая схема контроля признаёт пригодной стандартную продукцию с вероятностью 0,98 и нестандартную с вероятностью 0,05. Найти вероятность того, что изделие дважды прошедшее упрощённый контроль, удовлетворяет стандарту.

5.11. На сборку поступают детали из трёх цехов. Первый цех даёт 3% брака, второй – 2%, третий – 1%. Найти вероятность попадания бракованной детали на сборку, если каждый цех поставляет соответственно 500, 200 и 300 деталей.

5.12. Имеется пять винтовок, три из которых с оптическим прицелом. Вероятность поразить цель из винтовки с оптическим прицелом равна 0,95, из обычной – 0,8. Выбрав винтовку наугад, стрелок промахнулся. Какова вероятность того, что он стрелял из винтовки без оптического прицела?

5.13. В первом ящике находятся 6 белых и 4 чёрных шара, а во втором –
4 белых и 16 чёрных шаров. Из каждого ящика наудачу извлекли по одному шару. Затем из этих двух шаров случайным образом взяли один шар. Найти вероятности следующих событий: а) взятый шар – белый, б) извлечённые из ящиков шары – белые, если известно, что взятый из них наудачу шар, оказался белым.

5.14. Производится стрельба по цели тремя снарядами. Снаряды попадают в цель независимо друг от друга. Для каждого снаряда вероятность попадания в цель равна 0,4. Если в цель попал один снаряд, он поражает цель с вероятностью 0,3, если два снаряда – с вероятностью 0,7, если три снаряда – с вероятностью 0,9. Найти вероятность поражения цели.

5.15. В каждом из трёх ящиков находятся 1 белый и 2 чёрных шара. Из первого ящика случайным образом выбрали один шар и переложили во второй, тщательно перемешали шары, а затем переложили один шар из второго ящика в третий. Найти вероятности того, что в третий ящик был добавлен белый шар, если известно, что шар, взятый наугад из третьего ящика, оказался белым.

ФОРМУЛА БЕРНУЛЛИ

Если в каждом из n независимых испытаний вероятность появления события А одна и та же и равна p, то вероятность того, что в n испытаниях событие А появится k раз, находится по формуле Бернулли

, где .

6.1. Вероятность того, что расход электроэнергии за рабочий день на механическом заводе не будет превышать нормы равна 0,75. Найти вероятность того, что среди 6 рабочих дней окажется 2 дня, в течение которых произойдёт перерасход электроэнергии.

6.2. Производится 5 независимых выстрелов в одинаковых условиях. Вероятность попадания при каждом выстреле равна 0,8. Найти вероятность того, что будет более одного попадания.

6.3. Два спортсмена играют в настольный теннис. Вероятность выигрыша первого спортсмена равна 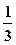. Какова вероятность того, что он выиграет 2 партии из 5?

6.4. Считая вероятности рождения человека по временам года одинаковыми, найти вероятность того, что из 6 человек не менее 5 родились зимой?

6.5. Производится 8 выстрелов по резервуару с горючим, причём первое попадание вызывает течь, а второе – воспламенение горючего. Какова вероятность того, что резервуар будет подожжен, если вероятность попадания при отдельном выстреле равна 0,2?

6.6. Отрезок АВ разделён точкой С в отношении 2:1. На этот отрезок наудачу «брошены» 4 точки. Найти вероятность того, что две из них окажутся левее точки С и две – правее. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

6.7. Система радиолокационных станций ведёт наблюдение за группой из
6 объектов. Каждый из них может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что будет потеряно от двух до трёх объектов.

6.8. В случайно выбранной семье четверо детей. Считая вероятности рождения мальчика и девочки одинаковыми, определить вероятность того, что в выбранной семье окажется: а) два мальчика и две девочки, б) более двух мальчиков.

6.9. Что вероятнее выиграть у равносильного противника: а) 3 партии из 4 или 5 из 8, б) не менее 3 партий из 4 или не менее 5 из 8?

6.10. Всхожесть семян данного сорта растений оценивается вероятностью равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырёх?