Числовые характеристики случайных величин

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ.

Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретныеи случайные непрерывные величины.

Дискретной называют величину, если она принимает счетное множество значений. (Пример: число пациентов на приеме у врача, число букв на странице, число молекул в заданном объеме).

Непрерывнойназывают величину, которая может принимать значения внутри некоторого интервала. (Пример: температура воздуха, масса тела, рост человека и т.д.)

Законом распределения случайной величины называется совокупность возможных значений этой величины и, соответствующих этим значениям, вероятностей (или частот встречаемости).

П р и м е р:

x	x1	x2	x3	x4	...	xn
p	р1	р2	р3	р4	...	pn

или

x	x1	x2	x3	x4	...	xn
m	m1	m2	m3	m4	...	mn

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.

Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры , получившие название числовых характеристик случайной величины. Наиболее употребительные из них:

1.Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:

2.Дисперсия случайной величины:

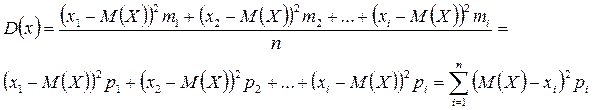
3.Среднее квадратичное отклонение:

Правило “ТРЕХ СИГМ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратичного отклонения