Вычисление определителей n-го порядка

Минором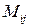элемента 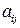, определителя 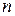-го порядка называется определитель ( 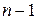)-го порядка, полученный из исходного определителя в результате вычеркивания 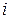-й строки и -го столбца, на пересечении которых стоит элемент .

Алгебраическим дополнениемэлемента 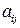определителя называется число .

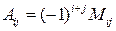Определитель 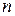-го порядка ( 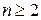) равен сумме произведений элементов 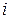-й строки на их алгебраические дополнения

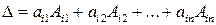(2.8)

или сумме произведений элементов -го столбца на их алгебраические дополнения

(2.9)

Равенства (2.8) и (2.9) называют формулами Лапласа разложения определителя по элементам 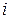-йстроки или -гостолбца.

Формулы (2.8) и (2.9) позволяют вычислить определитель n-го порядка разложением по любой его строке (столбцу). При этом вычисление определителя n-го порядка сводится к вычислению определителей ( 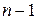)-го порядка. Затем вычисление каждого определителя ( 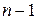)-го порядка сводится к вычислению определителей ( 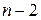)-го порядка и т.д. Таким образом, в результате последовательного использования формул Лапласа вычисление исходного определителя n-го порядка сводится к вычислению определителей второго или третьего порядка.

Кроме того, для вычисления определителей n-го порядка можно использовать метод приведения к треугольному виду. Этот метод заключается в преобразовании определителя к такому виду, где все элементы, лежащие по одну сторону от главной диагонали, равны нулю. В этом случае определитель равен произведению элементов главной диагонали.

Обратная матрица

Пусть – квадратная матрица. Матрица 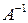называется обратнойпо отношению к матрице , если

, (2.10)

где – единичная матрица.

Для любой квадратной матрицы , определитель которой отличен от нуля, существует единственная обратная матрица. Обратная матрица имеет вид:

,

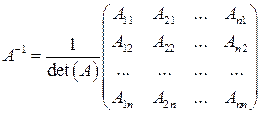где – алгебраические дополнения элементов 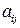, – определитель исходной матрицы .

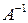Если , то обратная матрица не существует и матрица называется вырожденной.

Ранг матрицы

Рангом матрицы размерности 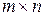называется наивысший порядок отличного от нуля минора, образованного из элементов этой матрицы. Ранг матрицы обозначают . При вычислении ранга матрицы переходят от миноров меньшего порядка, отличных от нуля, к минорам более высокого порядка. Для того, чтобы упростить процесс вычисления ранга матрицы, можно использовать элементарные преобразования матриц. Элементарными преобразованиями матрицы называются такие ее преобразования:

транспонирование матрицы;

отбрасывание нулевой строки (столбца) матрицы;

перестановка местами двух строк (столбцов);

умножение строки (столбца) на число, отличное от нуля;

прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на некоторое число.

Элементарные преобразования не изменяют ранга матрицы. Для нахождения ранга матрицы нужно элементарными преобразованиями привести эту матрицу к диагональному виду.

Ранг матрицы также можно вычислить методом окаймления миноров. Если уже найден ненулевой минор 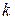-го порядка 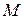, то достаточно вычислить только миноры 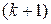-го порядка, окаймляющие минор 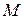. Если при этом все окаймляющие миноры равны нулю, то ранг матрицы равен .

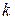Матрицы и 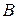, которые имеют равные ранги, называются эквивалентными матрицами. Эквивалентные матрицы обозначают .

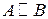Примеры решения задач

Пример 2.1. Даны матрицы и 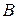. Найти матрицы 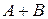и 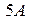, если

,

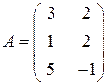Решение. По формуле (2.2) получаем

Из (2.3) следует, что

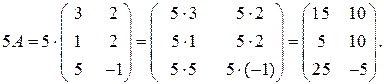
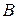Пример 2.2. Вычислить произведение матриц и , если

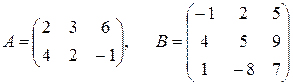
Решение. Так как размерности исходных матриц (2´3) и (3´3) соответственно, то матрицы и 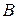можно перемножать (заметим, что произведение 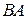не определено). При этом размерность матрицы 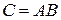будет равна (2´3).

Вычислим матрицу :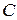

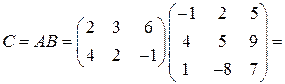
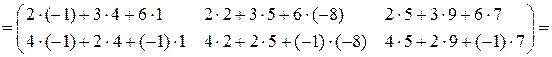
Пример 2.3. Вычислить определитель

Решение. Вычислим определитель по правилу треугольников:

Пример 2.4. Вычислить определитель

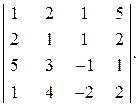
Решение. Для вычисления определителя используем формулу Лапласа (2.9) разложения определителя по элементам -го столбца. Вычисления существенно упростятся, если предварительно преобразовать определитель, получив в строке (столбце) нулевые элементы. При получении нулей в строке (столбце) удобно использовать любой элемент 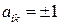. Разложим определитель по элементам первого столбца ( 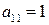), обратив предварительно элементы в нули. Все элементы первой строки умножим на (–2) и прибавим к соответствующим элементам 2-й строки.

Умножим элементы 1-й строки на 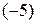и прибавим к соответствующим элементам второй строки

Теперь, умножив элементы 1-й строки на 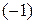, прибавим их к соответствующим элементам третьей строки

Полученный определитель раскладываем по элементам первого столбца

или окончательно

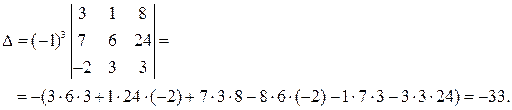
Пример 2.5. Вычислить определитель методом приведения к треугольному виду:

.

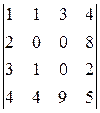Решение. Последовательно выполним следующие преобразования:

1. умножим элементы первой строки на (–2) и прибавим к соответствующим элементам второй строки;

2. умножим элементы первой строки на (–3) и прибавим к соответствующим элементам третьей строки;

3. умножим элементы первой строки на (–4) и прибавим к соответствующим элементам четвертой строки;

4. от элементов третьей строки отнимем соответствующие элементы второй строки;

5. от элементов четвертой строки отнимем соответствующие элементы третьей строки.

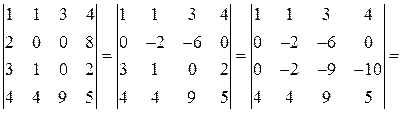
Пример 2.6. Найтиобратную матрицу для матрицы , сделать проверку, если

.

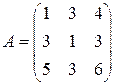Решение. Вычислим определитель матрицы :

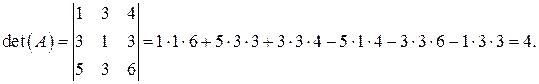
Поскольку , то существует обратная матрица 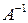. Найдем алгебраические дополнения для каждого элемента матрицы .

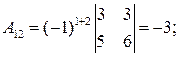
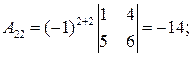
Тогда

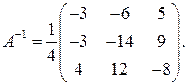
Сделаем проверку, умножив, например, обратную матрицу на исходную матрицу:

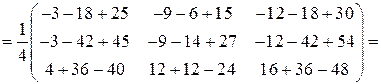
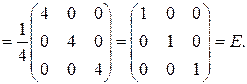
Пример 2.7. С помощью элементарных преобразований найти ранг матрицы

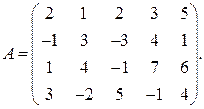
Решение. Выполним элементарные преобразования матрицы, не изменяющие ее ранга. Для удобства преобразований сначала поменяем местами первую и третью строки матрицы, тем самым получив в первой строке и первом столбце ведущий единичный элемент ( ):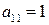

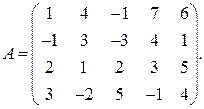
Теперь последовательно выполним следующие преобразования:

1. к элементам второй строки прибавим соответствующие элементы первой строки:

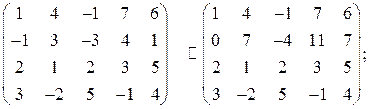
2. умножим элементы первой строки на (–2) и прибавим к соответствующим элементам третьей строки:

+

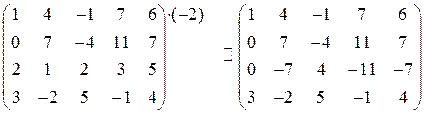
3. умножим элементы первой строки на (–3) и прибавим к соответствующим элементам четвертой строки:

.

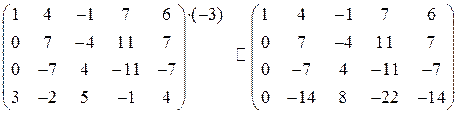Теперь прибавим к элементам третьей строки соответствующие элементы второй строки, а к элементам четвертой строки – соответствующие элементы второй строки, умноженные на 2.

.

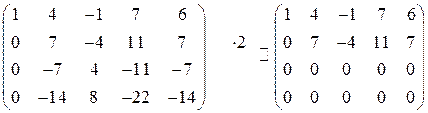Отбрасываем в последней матрице две нулевые строки:

.

Полученная матрица эквивалентна исходной и ее ранг не может быть выше двух. Находим в последней матрице любой ненулевой определитель второго порядка (если такой существует). Например, выбираем определитель, стоящий в верхнем левом углу:

.

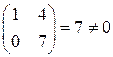Таким образом, существует ненулевой минор второго порядка, следовательно, ранг последней матрицы равен двум. Так как все проведенные преобразования не изменяют ранга матрицы, то исходная матрица также имеет ранг равный двум.

Пример 2.8.Найти ранг матрицы методом окаймления миноров, если

.

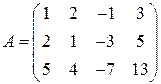Решение. В исходной матрице выбираем любой ненулевой минор второго порядка, например, минор, стоящий в верхнем левом углу:

.

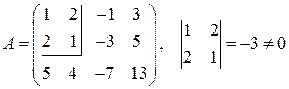Выписываем миноры третьего порядка, окаймляющие выбранный ненулевой минор второго порядка. Таких миноров два:

и .

Так как оба минора третьего порядка равны нулю, то ранг исходной матрицы равен двум.

Вопросы для самопроверки

2.1. Что такое числовая матрица?

2.2. Какая матрица называется квадратной?

2.3. Могут ли быть равны две матрицы разной размерности?

2.4. Как сложить две матрицы?

2.5. При каком условии можно перемножить две матрицы?

2.6. Как из исходной матрицы получить транспонированную?

2.7. Какое выражение называется определителем второго порядка? определителем третьего порядка?

2.8. Каковы основные свойства определителей?

2.9. Что называется минором и алгебраическим дополнением элемента матрицы?

2.10. Напишите формулы разложения определителя по элементам строки и столбца.

2.11. Каковы способы вычисления определителей?

2.12. Какая матрица называется обратной?

2.13. Для каких матриц существуют обратные?

2.14. Как найти обратную матрицу?

2.15. Что называется рангом матрицы?

2.16. Какие преобразования не изменяют ранга матрицы?

2.17. Как вычислить ранг матрицы с помощью метода окаймления миноров?

2.18. Какие матрицы называются эквивалентными?