Раздел III. Статика сооружений

ГЛАВА 1. ВВЕДЕНИЕ

Предмет строительной механики и ее задачи

Термин «строительная механика» применяют в широком и узком смысле этого слова.

В широком смысле слова строительная механика – это раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений. В этом значении она объединяет такие науки и дисциплины, как:

– теоретическая механика;

– сопротивление материалов;

– теория упругости;

– статика и динамика сооружений;

– металлические и железобетонные конструкции

и многое другое. При этом термин «строительная механика» близок к понятиям «прикладная» или «техническая механика».

В узком смысле слова строительная механика – это, прежде всего, статика сооружений, в дальнейшем именно так мы и будем понимать этот термин.

Напомним, что если предметом теоретической механики является абсолютно твердое тело (или система таких тел), а предметом сопромата – деформируемое тело, то предметом строительной механики является система деформируемых тел.

Основная задача строительной механики – проектирование сооружений, находящихся в определенных условиях, с учетом требований прочности, жесткости, устойчивости, надежности, экономичности, эстетики и других ограничений. Для решения этой задачи нужно построить модель сооружения, выделив основные несущие элементы и определив действующую на них нагрузку. Такая модель в виде совокупности деформируемых тел, соединенных друг с другом и с землей определенными связями, и называется расчетной схемой или системой.

В зависимости от геометрических особенностей элементов системы их делят на три класса: стержневые, тонкостенные и массивы. В общем случае расчетная схема может включать в себя каждый из этих элементов. Мы ограничимся в дальнейшем рассмотрением плоских стержневых систем.

Примечания

1. Помимо основной задачи – проектирования в строительной механике, как и в сопромате, может возникнуть необходимость расчета сооружения, уже находящегося в эксплуатации. Например – при его реконструкции.

2. Решение основной задачи строительной механики сводится, прежде всего, к определению внутренних усилий. Последующий подбор сечений элементов конструкции выполняется методами сопромата либо, в зависимости от вида материала – по теории железобетонных, металлических конструкций и т.д.

Кинематический анализ сооружений

Прежде чем приступить к расчету модели сооружения, необходимо проверить: способна ли она воспринимать приложенную нагрузку, оставаясь в равновесии? При этом расчетная схема рассматривается как совокупность не деформируемых, а абсолютно жестких тел – дисков, и в отдельный класс выделяются системы, элементы которых обладают подвижностью, то есть могут смещаться относительно друг друга или относительно земли. Такое исследование структуры модели называется ее кинематическим анализом.

Поскольку подвижность системы зависит, очевидно, от вида связей, соединяющих ее элементы, вернемся к рассмотрению и уточнению этих понятий – уже встречавшихся в теоретической механике.

Связи и их реакции

Напомним, что под связью понимают тело, ограничивающее свободу перемещения выбранного рассматриваемого тела, а реакцией связи называют силу, с которой связь действует на это тело.

Будем называть связь линейной, если соответствующая ей реакция – сила и моментной, если соответствующая ей реакция – момент.

Для плоских стержневых систем можно ограничиться рассмотрением следующих видов связей.

Подвижная опора (рис. 1.1) помимо обозначения по ГОСТ (рис. 1.1, а) может на схемах изображаться так, как показано на рис. 1.1, б и 1.1, в. Она соответствует одной линейной связи, а ее реакция перпендикулярна заштрихованной опорной площадке (рис. 1.1, г).

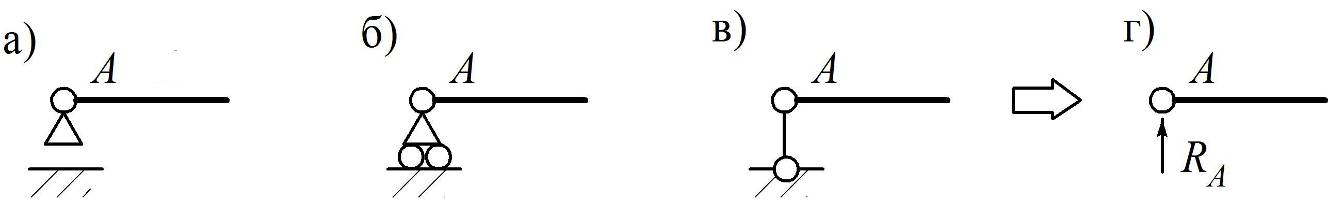
Рис. 1.1

Неподвижная опора (рис. 1.2) также допускает на схемах изображения, отличные от стандартного – на рис. 1.2, а. Очевидно, что она эквивалентна двум линейным связям (рис. 1.2, б–г).

Рис. 1.2

Жесткое защемление (рис. 1.3, а) исключает не только перемещения закрепленной таким образом точки конструкции, например – балки, но и ее поворот вокруг этой точки. Оно эквивалентно двум линейным связям и одной моментной (рис. 1.3, б), либо трем линейным связям при D ® 0 (рис. 1.3, в).

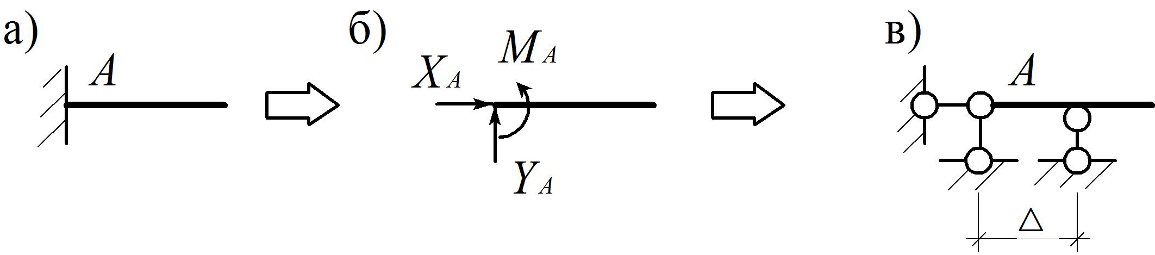
Рис. 1.3

Скользящее защемление (рис. 1.4, а–б) в отличие от жесткого не препятствует смещению закрепленной таким образом точки в одном из направлений и эквивалентно линейной и моментной связям (рис. 1.4, в) либо двум линейным при D ® 0 (рис. 1.4, г).

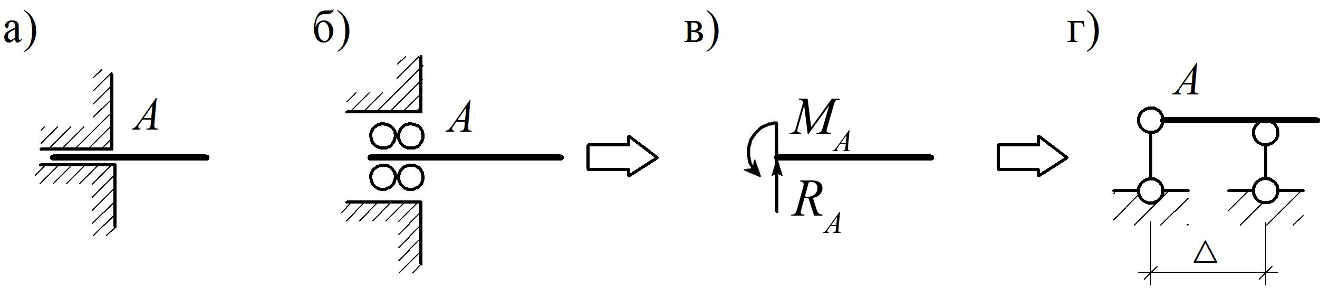
Рис. 1.4

Кратный шарнир, соединяющий N дисков, (рис. 1.5, а) будет эквивалентен (N – 1) простому шарниру (рис. 1.5, б).

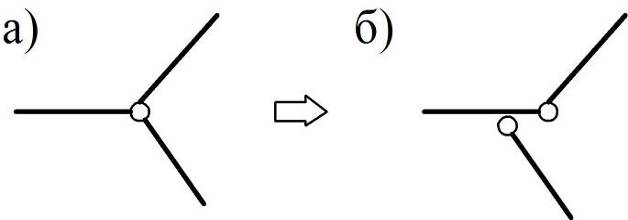
Рис. 1.5

Примечания

1. Результаты расчета можно улучшить, если учесть податливость соединений элементов системы.

2. Построение расчетной схемы действующего сооружения может оказаться непростой задачей, соизмеримой по сложности с самим расчетом.