Общие сведения о динамических воздействиях на грунт

Динамические воздействия на грунты и сооружения могут вызываться разными причинами:

• технологией ведения строительных работ(забивка шпунта

исвай, уплотнение грунта вибраторами и трамбовками);

•эксплуатационными и технологическими условиями (движение наземного и подземного транспорта);

•локальными инженерно-геологическимипроцессами(порывы ветра, удары волн, мощные взрывы и т.п.);

•современными тектоническими движениями в верхней части земной коры и проявляющимися на ее поверхности (землетрясения)

Динамические воздействия условно можно подразделить наслабые, которые могут часто действовать относительно длительное время, исильные, которые могут действовать кратковременно, возможно даже однократно (удар, взрыв). По времени действия усилия можно подразделить надлительно действующиеикратковременные.

35. Затухающая ползучесть

Существенное значение для практики имеет стадия затухающей ползучести и в некоторых случаях – стадия установившейся ползучести. Прогрессирующее же течение в основаниях сооружений ни в коем случае допускать нельзя, так как оно ведет к катастрофическим деформациям оснований.

Существует несколько теорий ползучести. Применение конкретной теории зависит от вида напряженного состояния материала и его структуры. Как показали опыты, для пылевато-глинистых грунтов удовлетворительные результаты дает теория линейной наследственной ползучести. Основными уравнениями при решении задач по этой теории являются: 1) уравнение напряженно-деформированного состояния грунтов и

2) уравнение сжимаемости газосодержащей поровой воды.

Уравнение напряженно- деформированного состояния грунтов при затухающей ползучести и однократном нагружении имеет вид:

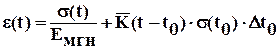, (6.13)

где: 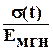- мгновенная деформация в момент 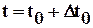; 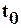- начальный
момент времени; 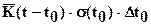- добавочная деформация, накопившаяся за время 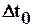от начала загружения грунта, пропорциональная начальному напряжению 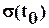, промежутку времени действия нагрузки 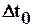и некоторой функции 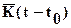, зависящей от времени, прошедшего с момента 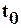(ядро ползучести).

При непрерывном загружении формула (6.13) принимает вид:

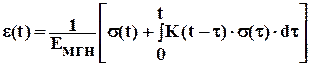, (6.14)

где: .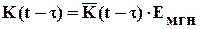

Ядро ползучести для дисперсных грунтов часто представляют в виде экспоненциальной зависимости, подтверждаемой экспериментами:

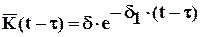, (6.15)

где 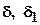- параметры ползучести (коэффициент ядра ползучести 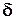и коэффициент затухания ползучести 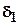), определяемые опытным путем.

◊ Определение параметров экспоненциального ядра ползучести

При определении параметров ползучести пылевато-глинистых грунтов для каждой ступени нагрузки определяют:

1) коэффициент начального порового давления

,

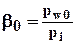где: 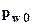- замеренное непосредственно после загрузки начальное поровое давление воды (нейтральное давление); 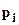- полное давление при данной ступени нагрузки;

2) коэффициент относительной сжимаемости грунта в стабилизированном конечном для данной ступени нагрузки состоянии (коэффициент конечной относительной сжимаемости) 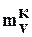, определяемый по формуле:

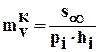, (6.16)

где: 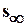- стабилизированная осадка грунта при данной ступени нагрузки; 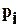- полное давление при данной ступени нагрузки; 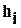- высота испытываемого слоя грунта при данной ступени нагрузки.

3) коэффициент относительной сжимаемости в момент приложения нагрузки (коэффициент первичной относительной сжимаемости) 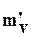, определяемый по формуле (которая вытекает из формулы (6.3)):

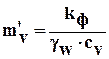, (6.17)

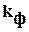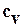где и коэффициенты фильтрации и консолидации в начале компрессионного уплотнения (например, при степени консолидаци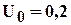и или ).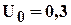

Далее определяют относительные скорости осадки образца за счет ползучести грунта для различных промежутков времени, а по ним – и величину коэффициента затухания ползучести 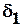. Для этого строят график (рис. 6.8) зависимости 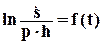, по которому определяют величину :

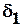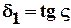. (6.18)

Здесь 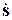- скорость осадки; 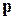- давление; 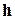- толщина деформирующегося слоя.

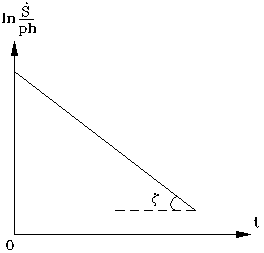
Рис. 6.8. Определение коэффициента затухания ползучести. Затем определяют вторичный коэффициент относительной сжимаемости (за счет ползучести скелета грунта) :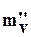

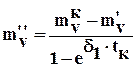, (6.19)

где 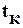- время полной стабилизации осадки при данной ступени нагрузки

Наконец вычисляют коэффициент ядра ползучести :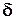

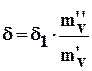. (6.20) .Так как процесс ползучести является продолжительным, для определения параметров ползучест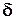и и 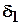требуется несколько дней.

36. Опытные исследования показали, что у различных грунтов осадка развивается по-разному. У некоторых грунтов осадка связана лишь с процессом фильтрационной консолидации, у других – фильтрационная консолидация и ползучесть развивается параллельно, у третьих – после завершения фильтрационной консолидации начинается ползучесть грунтов. Процесс развития осадки во времени зависит, главным образом, от следующих факторов:

- консолидации грунта;

- коэффициента водонасыщения ;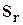

- порового давления ;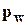

- характера приложения нагрузки (одноступенчатая, многоступенчатая).

Поэтому при расчете осадок во времени используют три основные модели грунта:

1) однокомпонентную (или квазиоднофаную) систему частиц;

2) двухкомпонентную (квазидвухфаную) систему частиц;

3) трехкомпонентную (трехфазную) систему частиц.

Квазиоднофазную модель используют при определении осадки в песчаных грунтах (влажных, сухих или водонасыщенных). Квазидвухфазную модель используют при определении осадки в пылевато-глинистых водонасыщенных грунтах. Трехфазная модель является наиболее общей, и ее используют при определении осадки в глинистых водонасыщенных ( 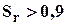) грунтах с учетом начального порового давления при начальном градиенте напора .

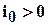◊ Определение осадки для квазиоднофазной модели

Предполагают, что осадка происходит только за счет ползучести скелета грунта при условии полного завершения процесса фильтрационной консолидации. Так как ядро ползучести (6.15)

представляет собой скорость ползучести грунта при постоянном единичном напряжении, то ползучесть скажется лишь при протекании осадок во времени, а полня стабилизированная осадка будет иметь прежнее выражение:

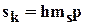, (6.21)

где 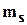- коэффициент относительной сжимаемости скелета грунта при ползучести, вычисляемый по формуле:

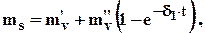(6.22)

где 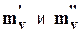- коэффициенты первичной и вторичной консолидации грунта.

Так как смогласно формуле (6.20)

,

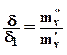то, подставляя (6.22) в (6.21), получим выражение для полной осадки:

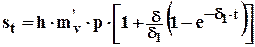. (6.23)

В случае действия местной нагрузки вместо величины 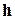следует подставить значение эквивалентного слоя .

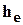38. Практические исследования волновых процессов в грунтах при динамических воздействиях – на измерении расчетных схем, рассматривающих обобщенные свойства грунтов с приближением к натуре, позволяющим описать их математически. В настоящее время – это модели: предельно упругой среды (линейной и нелинейной), среды (Х.А. Рахматулина), модели вязкопластичной среды (Ляхов), нелинейная дилатационная модель (А.П. Синицын).

Наиболее характерные кривые изменения динамических нагрузок во времени, вызываемых работой машин:

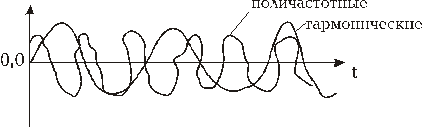
периодические нагрузки. Гармонические: турбоагрегаты, роторы, другие машины с вращающимися частями. Поличастотные: машины с кривошипно-шатунными механизмами (поршневые компрессоры).

непериодические нагрузки. Импульсные – кузнечные молоты. Сложные – приводной двигатель прокатного стана.

39. Явления, происходящие в грунтах при динамических воздействиях

Для рыхлых несвязных грунтов характерно явление виброкомпрессии, что выражается в виброуплотнении песков вплоть до плотного состояния, если грунт не был пригружен. При наличии внешней пригрузки уплотнение песка будет происходить только при сообщаемых грунту ускоренях колебаний, превышающих так называемые критические, причем полного уплотнения песка все же не достигается (Цытович, 1973). При высоком уровне динамических воздействий водонасыщенные песчаные грунты обнаруживают способность к разжижению, сопровождаемому полной потерей устойчивости грунтов. Подобные явления наблюдаются при сильных землетрясениях, когда относительно жесткие здания погружаются в грунт на несколько метров, зачастую со значительными кренами.

Глинистые грунты ввиду наличия связности более устойчивы к динамическим воздействиям, чем песчаные. Однако при пластичной и текучей консистенции этих грунтов динамические нагрузки могут вызывать разрушение их структуры, что необходимо исключать при проектировании и строительстве.

Вместе с тем необходимо отметить, что наблюдаемые при сильных землетрясениях явления разжижения песков и разрушения структуры связных грунтов не могут исчерпывающе объяснять случаи опрокидывания жестких зданий, принимающих после окончания сейсмических толчков почти горизонтальное положение (землетрясения в Ниигата и на Тайване). Для удовлетворительной оценки динамической устойчивости зданий помимо изучения условий разрушения грунтов оснований при распространении пластических волн в грунтах следует учитывать также условия динамического равновесия сил, приложенных к фундаменту при бегущих сейсмических волнах. Решение этой задачи показывает, что при прохождении волны под зданием оно начинает раскачиваться, а в отдельных зонах под фундаментом имеет место резкое увеличение контактных давлений (Синицин, 1978). Очевидно, именно этим обусловлена полная потеря несущей способности грунтов основания зданий, конструкции которых, включая фундаменты, проектировались с учетом антисейсмических требований. В этом случае упомянутые в разд. 11.1 динамические расчеты сооружений и грунтов необходимо производить совместно.

Отмеченные эффекты виброкомпрессии песков или даже их разжижения наблюдаются при интенсивных динамических воздействиях. Однако многочисленные наблюдения показывают, что и в случае весьма малых сотрясений фундаменты существующих зданий и сооружений могут претерпевать длительные незатухающие осадки, достигающие нескольких миллиметров в год. Это свойство грунтов накапливать микроскопические деформации в допредельном состоянии называется виброползучестью. Таким образом, динамические воздействия на грунты вызывают распространение волн и колебания оснований и сооружений. Эти колебания могут быть неблагоприятны для людей и ряда высокоточных производственных процессов, а при совпадении свободных и вынужденных частот колебаний (в условиях резонанса) представлять угрозу целостности сооружений. Подверженные колебаниям грунты основания могут доуплотняться, а при определенных условиях и разжижаться, то есть полностью терять устойчивость.