Кратные и криволинейные интегралы
Методические указания по организации самостоятельной работы
для студентов 1 и 2-го курсов трансферных специальностей
Краснодар
УДК 519.1 (0.75.8)+512
Составители:
Канд. физ.-мат. наук доц. С.Н. Горшкова, ст. преп. И.И. Петрушина
Кратные и криволинейные интегралы: Методические указания по организации самостоятельной работы для студентов 1 и 2-го курсов трансферных специальностей. / Сост.: С.Н. Горшкова, И.И. Петрушина. Ин-т совр. технол. и эконом. – Краснодар, 2005, … с.
Методические указания предназначены для студентов 1 и 2-го курсов трансферных специальностей, изучающих курс математического анализа. Даны понятия кратных интегралов, переход от них к повторным, понятия криволинейных интегралов, переход от них к определенным, приведена общая схема их конструкции, подробно рассмотрено и проанализировано решение всех типов задач, связанных с криволинейными и кратными интегралами. Приведены индивидуальные типовые задания по теме.
Работа подготовлена по результатам НИР «Научно-методическое обеспечение содержания образования».
Ил. … Библиогр. … назв.
Печатается по решению Редакционно-издательского совета Института современных технологий и экономики.
Рецензенты:
канд. техн. наук, доц. Л.М. Данович
канд. техн. наук, доц. А.С. Арутюнян
Двойной интеграл
Понятие двойного интеграла
Рассмотрим в плоскости Оху область σ, имеющую конечную площадь и ограниченную одной или несколькими линиями. Пусть в этой области σ задана функция  . Составим для этой функции интегральную сумму вида
. Составим для этой функции интегральную сумму вида
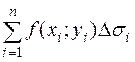 , (1)
, (1)
где Δσi – элементарные площадки, получаемые при произвольном делении области σ на n частей, Pi(xi;yi) – точки, произвольно выбираемые на каждой из этих частей. Условимся области и их площади обозначать одинаковыми буквами.
Диаметром замкнутой области называется наибольшее из расстояний между двумя точками границы этой области.
Шагом разбиения области называется наибольший из диаметров элементарных частей Δσi \ λ – шаг разбиения\. Интегральная сумма зависит от способа разбиения области на элементарные части, от выбора точек Pi , от области σ , от вида функции  . Рассмотрим предел последовательности интегральных сумм (1) при стремлении λ к нулю, т.е. при неограниченном увеличении числа элементарных частей и при стягивании каждой из них в точку.
. Рассмотрим предел последовательности интегральных сумм (1) при стремлении λ к нулю, т.е. при неограниченном увеличении числа элементарных частей и при стягивании каждой из них в точку.
Если существует конечный предел при 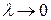 последовательности интегральных сумм (1), не зависящий ни от способа разбиения области на элементарные части Δσi , ни от выбора на каждой из них точек Pi(xi;yi) , то этот предел называется двойным интегралом от функции
последовательности интегральных сумм (1), не зависящий ни от способа разбиения области на элементарные части Δσi , ни от выбора на каждой из них точек Pi(xi;yi) , то этот предел называется двойным интегралом от функции  по области σ и обозначается
по области σ и обозначается
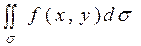
То есть
 (2)
(2)
Функция, для которой такой предел существует, называется
интегрируемой в области σ,  - подынтегральная функция,
- подынтегральная функция, 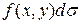 - подынтегральное выражение, σ – область интегрирования.
- подынтегральное выражение, σ – область интегрирования.
Геометрический смысл двойного интеграла
Пусть функция  непрерывна в области σ и
непрерывна в области σ и 
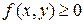 . Рассмотрим тело, ограниченное снизу областью σ плоскости Оху, сверху – поверхностью, заданной уравнением
. Рассмотрим тело, ограниченное снизу областью σ плоскости Оху, сверху – поверхностью, заданной уравнением  , сбоку – цилиндрической поверхностью с образующими, параллельными оси Oz. Такое тело называется цилиндрическим. В этом случае двойной интеграл имеет простое геометрическое толкование.
, сбоку – цилиндрической поверхностью с образующими, параллельными оси Oz. Такое тело называется цилиндрическим. В этом случае двойной интеграл имеет простое геометрическое толкование.
Объем рассмотренного тела равен сумме объемов цилиндрических столбиков с основанием Δσi , он приближенно равен сумме произведений площадей оснований  на высоты
на высоты  ,
,  , где hi – равны значению функции в произвольно выбранных точках. А это есть интегральная сумма (1).
, где hi – равны значению функции в произвольно выбранных точках. А это есть интегральная сумма (1).
Точное значение объема дает предел этой суммы при 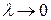 , то есть двойной интеграл:
, то есть двойной интеграл:
 (3)
(3)
То есть, двойной интеграл численно равен объему цилиндрического тела.
Существование двойного интеграла
Для 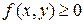 существование двойного интеграла кажется очевидным, так как он дает объем тела. В общем случае предел вида (2) существует не для всех функций.
существование двойного интеграла кажется очевидным, так как он дает объем тела. В общем случае предел вида (2) существует не для всех функций.
Теорема. Для всякой функции  , непрерывной в ограниченной замкнутой области, имеющей площадь σ , существует двойной интеграл по этой области.
, непрерывной в ограниченной замкнутой области, имеющей площадь σ , существует двойной интеграл по этой области.
Вычисление двойного интеграла в декартовых координатах.
Вычислять двойной интеграл, как предел интегральной суммы (2), очень трудно. Чтобы избежать вычислительных трудностей, двойной интеграл сводят к последовательному вычислению двух определённых интегралов.
Посчитаем, что подынтегральная функция  , это позволит рассматривать двойной интеграл численно равным объёму цилиндрического тела.
, это позволит рассматривать двойной интеграл численно равным объёму цилиндрического тела.

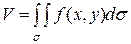 (3)
(3)
Предположим, что область интегрирования ограничена двумя непрерывными кривыми
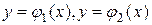 и двумя прямыми
и двумя прямыми 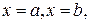 причём при
причём при

Пусть x – произвольная точка, принадлежащая 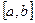 , проведём через неё прямую, параллельную оси Oy. Эта прямая пересекает кривые
, проведём через неё прямую, параллельную оси Oy. Эта прямая пересекает кривые 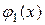 и
и 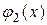 в точках c1 и с2. Их ординаты Yвхода и Yвыхода, тогда
в точках c1 и с2. Их ординаты Yвхода и Yвыхода, тогда
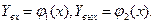
Теперь посчитаем объём тела с помощью метода поперечных сечений. Известно, что
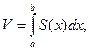 (4)
(4)
 где S(x) – площадь поперечного сечения.
где S(x) – площадь поперечного сечения.
Выберем произвольную точку (x,o,o) и проведём через неё плоскость, перпендикулярную оси Ox, тогда в поперечном сечении получится криволинейная трапеция. Чтобы воспользоваться формулой (4), найдём площадь криволинейной трапеции в этом случае.
Из геометрического смысла определённого интеграла известно, что площадь криволинейной трапеции вычисляется по формуле
 (5)
(5)
где 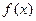 -функция одной переменной x. Для нашего случая: если абсциссу х зафиксировать, то аппликата точек линии M1M2 зависит только от у, то есть функция
-функция одной переменной x. Для нашего случая: если абсциссу х зафиксировать, то аппликата точек линии M1M2 зависит только от у, то есть функция 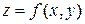 есть функция одного переменного у, и можно применить формулу (5), y изменяется в этом случае от
есть функция одного переменного у, и можно применить формулу (5), y изменяется в этом случае от 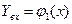 до
до 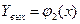 , тогда
, тогда
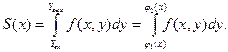
Подставляя это выражение в равенство (4), получаем
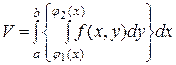
или
 . (6)
. (6)
Из формулы (3) и (6) следует
 (7)
(7)
Таким образом, чтобы вычислить двойной интеграл, нужно сначала вычислить внутренний интеграл

Считается при этом, что x – постоянная величина. Так как 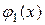 и
и 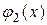 есть функции, зависящие от x, то результатом вычисления интеграла будет функция, зависящая только от x. Её и нужно проинтегрировать в пределах от a до b. Полученное число и будет значением двойного интеграла.
есть функции, зависящие от x, то результатом вычисления интеграла будет функция, зависящая только от x. Её и нужно проинтегрировать в пределах от a до b. Полученное число и будет значением двойного интеграла.
Пример I. Вычислить в декартовых координатах
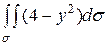 ,
,
где  - область в плоскости Oxy, ограниченная линиями
- область в плоскости Oxy, ограниченная линиями 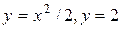 .
.
 Решение
Решение
Другими словами, надо найти объём тела, ограниченного сверху поверхностью
Z = 4 - y2.
Это параболический цилиндр, развёрнутый вниз “ветвями” и поднятый вверх на 4 единицы. Вычертим теперь область  . Для этого вспомним, что она лежит в плоскости Oxy, то есть z = 0. Тогда из уравнения поверхности при z = 0 получаем y2 = 4,
. Для этого вспомним, что она лежит в плоскости Oxy, то есть z = 0. Тогда из уравнения поверхности при z = 0 получаем y2 = 4,
y = ±2. Кроме того, надо рассмотреть все линии, уравнения которых не содержит z. Эти линии ограничивают область  . Подставив
. Подставив
y = 2 в уравнение  , получаем
, получаем
x2 = 4, x = ±2. Возьмём произвольную точку
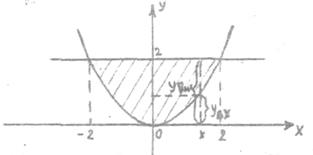 (x,0,0), проведём плоскость, перпендикулярную оси Ox, сечением будет криволинейная трапеция z = 4 – y2, в области
(x,0,0), проведём плоскость, перпендикулярную оси Ox, сечением будет криволинейная трапеция z = 4 – y2, в области  переменная x изменяется от
переменная x изменяется от
-2 до +2, переменная y меняется от
yвх = x2/2 до yвых = 2, поэтому
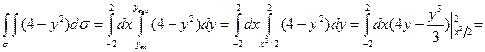

Замечание. Ввиду симметричности области  , можно считать
, можно считать 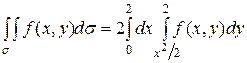
Таким образом, вычисление двойного интеграла сводится к последовательному вычислению двух определённых интегралов.
Замечания.
I. Если область интегрирования ограничена двумя непрерывными кривыми
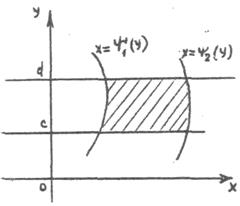
 и двумя горизонтальными прямыми y = c, y = d, c < d
и двумя горизонтальными прямыми y = c, y = d, c < d
 ,то, рассуждая аналогично, можно получить
,то, рассуждая аналогично, можно получить
 (8)
(8)
В этом случае при вычислении внутреннего интеграла считаем y постоянной величиной. Результатом этого будет функция, зависящая от y, так как пределы внутреннего интеграла зависят от y. Потом полученную функцию интегрируем в пределах от c до d.
Интегралы, стоящие в правых частях формул (7), (8), называются повторными или двукратными.
2. В формулах вида (7), (8) пределы внешнего интеграла всегда постоянные.
 3. Формулы (7), (8) выведены в предположении, что
3. Формулы (7), (8) выведены в предположении, что  имеет специальный вид. Если контур области более сложный, то её разбивают на конечное число областей, удовлетворяющих условиям, выдвинутым при выводе формул (7), (8), и интеграл по области
имеет специальный вид. Если контур области более сложный, то её разбивают на конечное число областей, удовлетворяющих условиям, выдвинутым при выводе формул (7), (8), и интеграл по области  представляют в виде суммы интегралов по слагаемым областям
представляют в виде суммы интегралов по слагаемым областям 
4.Рассмотрим цилиндрическую систему координат, в ней положение точки в пространстве определяется полярными координатами  её проекции на плоскость Oxy и её аппликатой z:
её проекции на плоскость Oxy и её аппликатой z:

Тогда
 (9)
(9)
Переход к цилиндрическим координатам часто существенно упрощает вычислительную работу.
Пример 2. Вычислить
 ,
,
где  - область, ограниченная линией x2 + y2 = 4.
- область, ограниченная линией x2 + y2 = 4.
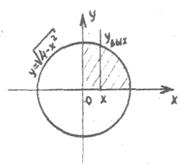
Вычертим цилиндрическое тело, ограниченное сверху поверхностью z = x2 + y2 снизу – кругом x2 + y2 =4, R = 2. Покажем отдельно область  . Ввиду симметрии тела, можно рассматривать его четверть. Возьмём произвольную точку (x,0,0) и проведём через неё плоскость, перпендикулярную оси Ox, получим в сечении криволинейную трапецию
. Ввиду симметрии тела, можно рассматривать его четверть. Возьмём произвольную точку (x,0,0) и проведём через неё плоскость, перпендикулярную оси Ox, получим в сечении криволинейную трапецию
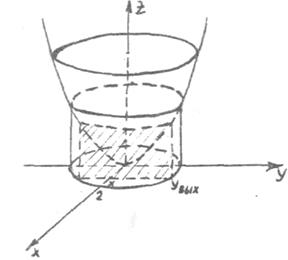 z = x2 + y2
z = x2 + y2
где z зависит только от y
/x - фиксирована/.
В области  переменная x меняется от 0 до 2 /мы рассматриваем только четверть/, переменная y меняется от yвх = 0 до
переменная x меняется от 0 до 2 /мы рассматриваем только четверть/, переменная y меняется от yвх = 0 до 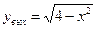
 Тогда используем формулу (7), (9), получаем x2 + y2 = 4
Тогда используем формулу (7), (9), получаем x2 + y2 = 4

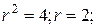

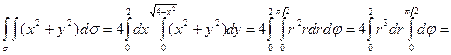
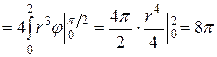 .
.
Вычисление площадей плоских фигур с помощью двойного интеграла.
Из определения двойного интеграла следует, что при 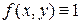 значение двойного интеграла по области
значение двойного интеграла по области  численно равно площади области
численно равно площади области  :
:

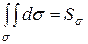
Пример 3.
Вычислить площадь, ограниченную следующими линиями:
x = 0, x = 1, y = x, y=2 – x2.
Решение: 
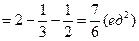
Вычисление объёмов тел с помощью двойных интегралов.
Наиболее сложный этап в задачах такого типа – это построение тела, объём которого необходимо найти /см. примеры 1,2/. Попытаемся вычислять объём тела без точного вычерчивания чертежа. Проанализируем, что нужно для определения объёма тела.

Необходимо знать поверхность z = f(x,y), ограничивающую тело сверху, область  , ограничивающую его снизу. Уравнение поверхности всегда задано в условии. Область
, ограничивающую его снизу. Уравнение поверхности всегда задано в условии. Область  можно построить, вспомнив, что она расположена в плоскости oxy, то есть в плоскости z = 0, то есть f(x,y) = 0 и выяснить, какая линия получилась. И дополнительно, если они даны в условии, рассмотреть линии, лежащие в плоскости Oxy. Эти линии определены уравнениями, не содержащими z. Все эти линии ограничивают искомую область
можно построить, вспомнив, что она расположена в плоскости oxy, то есть в плоскости z = 0, то есть f(x,y) = 0 и выяснить, какая линия получилась. И дополнительно, если они даны в условии, рассмотреть линии, лежащие в плоскости Oxy. Эти линии определены уравнениями, не содержащими z. Все эти линии ограничивают искомую область  .
.
Продемонстрируем это на примере.
Пример 4.
Вычислить объём тела, ограниченного поверхностями
x = 1 – z2, y = x, y = -x
Решение
 Найдём область
Найдём область  - она ограничивает тело снизу. Для этого положим z = 0, тогда x = 1 –это прямая, параллельная оси Oy. Кроме того, рассмотрим прямые, определяемые уравнениями, не содержащими в своих уравнениях z: y = x, y = -x Построим эти прямые. Область, заключённая между ними, и есть область
- она ограничивает тело снизу. Для этого положим z = 0, тогда x = 1 –это прямая, параллельная оси Oy. Кроме того, рассмотрим прямые, определяемые уравнениями, не содержащими в своих уравнениях z: y = x, y = -x Построим эти прямые. Область, заключённая между ними, и есть область  . Найдём теперь поверхность z = f(x,y), ограничивающую тело сверху. Для этого из уравнения, содержащего z, выразим его:
. Найдём теперь поверхность z = f(x,y), ограничивающую тело сверху. Для этого из уравнения, содержащего z, выразим его:  Ввиду симметрии тела /см. область/ можно вычислить четверть объёма V /по заштрихованной части/. Возьмём в этой части произвольную точку x и проведём через неё прямую, параллельную оси Oy. В этом случае x изменяется в пределах от 0 до 1, y изменяется от 0 до yвых = x.
Ввиду симметрии тела /см. область/ можно вычислить четверть объёма V /по заштрихованной части/. Возьмём в этой части произвольную точку x и проведём через неё прямую, параллельную оси Oy. В этом случае x изменяется в пределах от 0 до 1, y изменяется от 0 до yвых = x.
Поэтому

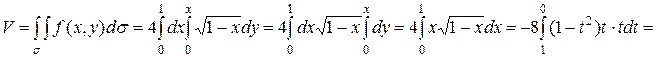
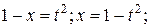
 .(ед3)
.(ед3)
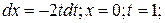

 Пример 5.
Пример 5.
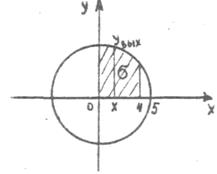
Найти объём тела, ограниченного поверхностями
z = y, z = 0, x = 0, x = 4, x2 + y2 =25
Решение.
Сверху тело ограничено поверхностью z = y, снизу – областью  .
.
Найдём её, как пересечение поверхности z = f(x,y) и плоскости z = 0. Тогда из уравнения поверхности получаем y = 0 – это ось Ox. Кроме того, рассматриваем линии, заданные уравнениями, не содержащими z: x = 0, x = 4,
x2 + y2 =25, x =0 – это ось Oy, x =4 – прямая, параллельная оси Oy, x2 + y2 =25 – окружность радиуса R = 5, y = 0 – ось Ox. Часть плоскости, ограниченная этими линиями, есть область  . Возьмём в этой области по оси Ox произвольную точку х и проведём через неё прямую, параллельную оси Oy. Тогда в области
. Возьмём в этой области по оси Ox произвольную точку х и проведём через неё прямую, параллельную оси Oy. Тогда в области  переменная x изменяется от 0 до 4, переменная y изменяется от 0 до окружности, то есть до
переменная x изменяется от 0 до 4, переменная y изменяется от 0 до окружности, то есть до 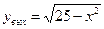
Поэтому
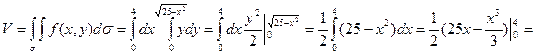

Замечание.
Иногда для облегчения вычислительной работы удобно в двойном интеграле изменить порядок интегрирования.
Пример 6.Изменить порядок интегрирования в двойном интеграле.
Решение.
Дан интеграл 
Чтобы изменить порядок интегрирования следует изобразить область интегрирования. Это можно сделать, если будут известны уравнения линий, ограничивающих эту область. Чтобы получить уравнения линий, ограничивающих область интегрирования, надо пределы интеграла по dx приравнять x, а пределы интеграла по dy приравнять y.
Для нашего случая
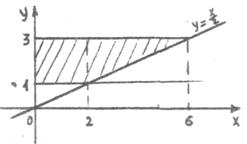 x = 1. x = 2,
x = 1. x = 2,
y = 1, y = 3,
x = 2, x = 6,
y = x/2, y = 3
Тогда y изменяется от 1 до 3, x изменяется от 0 до xвых = 2y
Поэтому
 .
.
Тройной интеграл.
Пусть в пространстве задано тело, объём которого равен V. Предположим, что в каждой точке этого объёма определена функция 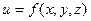
1. Разобьем тело на n малых тел  причём
причём  /в дальнейшем V и
/в дальнейшем V и  обозначают как тела, так и их объёмы/.
обозначают как тела, так и их объёмы/.
2. В каждом из малых тел выбираем произвольным образом по точке 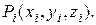 Умножим значение функции
Умножим значение функции  в каждой точке
в каждой точке 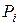 на соответствующий объём
на соответствующий объём  малого тела, которому принадлежит точка
малого тела, которому принадлежит точка 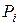 :
: 
3. Составим сумму таких произведений
 которая называется интегральной суммой.
которая называется интегральной суммой.
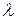 - как и прежде, диаметр наибольшего из разбиений
- как и прежде, диаметр наибольшего из разбиений  .
.
Если существует предел последовательности интегральных сумм при 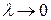 , не зависящий ни от способа разбиения объёма
, не зависящий ни от способа разбиения объёма  на части
на части  , ни от выбора в каждом из них точки
, ни от выбора в каждом из них точки 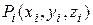 , то это число называют тройным интегралом от функции
, то это число называют тройным интегралом от функции  по области
по области  и обозначают
и обозначают
 или
или 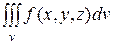
То есть

Видно, что тройной интеграл является непосредственным обобщением двойного интеграла на случай, когда областью интегрирования является тело трёх измерений.
Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов аналогично тому, как это было сделано для двойного интеграла.
Вычисление объёма тел с помощью тройных интегралов.
Если в тройном интеграле подынтегральная функция  , то тройной интеграл численно равен объёму тела V. /Следует помнить, что мы одной буквой обозначаем и область, и её объём./
, то тройной интеграл численно равен объёму тела V. /Следует помнить, что мы одной буквой обозначаем и область, и её объём./
 .
.
Этот интеграл далее сводим к повторным интегралам, пределами которых будут пределы изменения переменных x, y, z в данном теле V.
Пример 7.
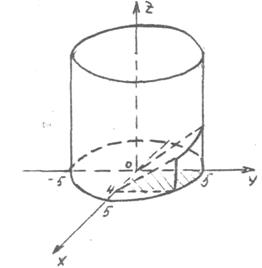
С помощью тройного интеграла вычислить объём тела, ограниченного поверхностями;
z = y, z = 0, x = 0, x = 4, x2 + y2 = 25
 Решение.
Решение.
 Вначале покажем решение такого типа задач с построением тела. x2 + y2 = 25 – на плоскости Oxy это окружность, в пространстве – круговой цилиндр, x = 4 – на плоскости прямая, в пространстве – плоскость, параллельная плоскости Oyz, x= 0 –плоскость Oyz, z = y – на плоскости Oyz – это биссектриса, в пространстве – плоскость. Тогда можно вычислить тело V. В этом теле переменная x изменяется от 0 до 4, переменная y изменяется от 0 до окружности x2 + y2 = 25, то есть до
Вначале покажем решение такого типа задач с построением тела. x2 + y2 = 25 – на плоскости Oxy это окружность, в пространстве – круговой цилиндр, x = 4 – на плоскости прямая, в пространстве – плоскость, параллельная плоскости Oyz, x= 0 –плоскость Oyz, z = y – на плоскости Oyz – это биссектриса, в пространстве – плоскость. Тогда можно вычислить тело V. В этом теле переменная x изменяется от 0 до 4, переменная y изменяется от 0 до окружности x2 + y2 = 25, то есть до 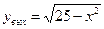 , /см. пример 5/, переменная z изменяется от 0 /плоск. z = 0/ до накрывающей тело поверхности
, /см. пример 5/, переменная z изменяется от 0 /плоск. z = 0/ до накрывающей тело поверхности 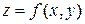 , то есть до z = y.
, то есть до z = y.
Тогда 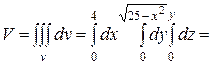
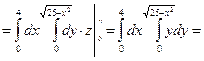
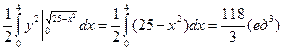
 Пример 8.
Пример 8.
Найти объём тела, ограниченного поверхностями:
z = 0, z = y2, x – y = 0, x + y =2
Решение.
Решим задачу, не прибегая к точному построению тела.
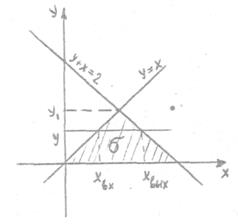
Поверхность z = f(x,y), ограничивающая тело сверху, есть z = y2. Снизу тело ограничено областью  . Вычертим её. Для этого положим в уравнении поверхности z = 0, тогда y2 = 0, то есть y = 0, и рассмотрим линии, уравнения которых не содержат z: x – y = 0, x + y = 2.
. Вычертим её. Для этого положим в уравнении поверхности z = 0, тогда y2 = 0, то есть y = 0, и рассмотрим линии, уравнения которых не содержат z: x – y = 0, x + y = 2.
Построим линии: y = 0, y = x, y = 2 – x
Они ограничивают область  . Для такой области удобнее взять внешний интеграл по переменной y, в противном случае, вместо одного пришлось бы вычислять два интеграла. В области
. Для такой области удобнее взять внешний интеграл по переменной y, в противном случае, вместо одного пришлось бы вычислять два интеграла. В области  переменная y изменяется от 0 до y1. Найдем y1 как ординату точки пересечения прямых y = x и y = 2 – x.
переменная y изменяется от 0 до y1. Найдем y1 как ординату точки пересечения прямых y = x и y = 2 – x.
Имеем: 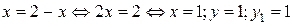 .
.
Тогда в области  переменная y изменяется от 0 до 1. Возьмём на этом промежутке производную точку y и проведём через неё прямую, параллельную оси Ox, тогда переменная x в области
переменная y изменяется от 0 до 1. Возьмём на этом промежутке производную точку y и проведём через неё прямую, параллельную оси Ox, тогда переменная x в области  изменяется от xвх до xвых; xвх – это абсцисса x прямой y = x, то есть xвх = y, а xвых – это абсцисса прямой x + y = 2. Из этого уравнения xвых = 2- y. Аппликата z в теле V изменяется от плоскости z = 0, то есть от 0 до накрывающей тело поверхности z = y2. Поэтому:
изменяется от xвх до xвых; xвх – это абсцисса x прямой y = x, то есть xвх = y, а xвых – это абсцисса прямой x + y = 2. Из этого уравнения xвых = 2- y. Аппликата z в теле V изменяется от плоскости z = 0, то есть от 0 до накрывающей тело поверхности z = y2. Поэтому:


Криволинейный интеграл второго рода.
Векторным полем называется область, каждой точке которой поставлен в соответствие вектор 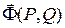 , проекции которого на координатные оси являются функциями координат точки M(x,y). P = P(x,y), Q = Q(x,y), то есть
, проекции которого на координатные оси являются функциями координат точки M(x,y). P = P(x,y), Q = Q(x,y), то есть  -вектор-функция. /Аналогично в пространстве/.
-вектор-функция. /Аналогично в пространстве/.
Пусть в некоторой области задана кривая L /дуга AB/ и вектор-функция  , определённая в каждой точке кривой L.
, определённая в каждой точке кривой L.
1. Разобьем дугу AB точками A0, A1, …, An на n дуг. Пусть (xi,yi) – координаты точек Ai(i=0,1, …,n); 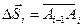
2. На каждой дуге выбираем произвольным образом по точке 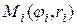 . Составим скалярное произведение вектора
. Составим скалярное произведение вектора  , взятого в точке Mi на вектор
, взятого в точке Mi на вектор 
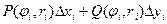 .
.
3. Составим сумму таких произведений /интегральную сумму/ и перейдём к пределу при 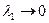 .
.  - длина наибольшего из звеньев ломанной, вписанной в дугу,
- длина наибольшего из звеньев ломанной, вписанной в дугу, 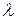 - длина наибольшего из звеньев дуг
- длина наибольшего из звеньев дуг  . При
. При  ,
, 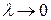 и каждая из дуг стягивается в точку.
и каждая из дуг стягивается в точку.
Предел этой интегральной суммы при 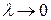 , не зависящий от способа разбиения дуги АВ на элементарные части и от выбора на каждой из них точек Mi , называется криволинейным интегралом II рода или по координатам:
, не зависящий от способа разбиения дуги АВ на элементарные части и от выбора на каждой из них точек Mi , называется криволинейным интегралом II рода или по координатам:

Вычисление криволинейного интеграла второго рода
I. Пусть дуга L задана параметрическими уравнениями
 ,
,  ,
, 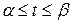
Причем функции x(t), y(t) непрерывны и имеют непрерывные производные первого порядка при  . Пусть начальной точке А дуги АВ соответствует значение параметра t= α , конечной точке В соответствует значение t= β и при изменении t от α до β переменная точка M(x,y) описывает дугу в направлении от точки А к точке В. P(x,y), Q(x,y) – непрерывные функции. Тогда эти сложные функции P[x(t),y(t)]; Q[x(t),y(t)] – непрерывны при
. Пусть начальной точке А дуги АВ соответствует значение параметра t= α , конечной точке В соответствует значение t= β и при изменении t от α до β переменная точка M(x,y) описывает дугу в направлении от точки А к точке В. P(x,y), Q(x,y) – непрерывные функции. Тогда эти сложные функции P[x(t),y(t)]; Q[x(t),y(t)] – непрерывны при  .
.
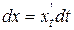 ,
, 
и получаем формулу, позволяющую свести вычисление криволинейного интеграла II рода к вычислению определенного интеграла:

2. Если плоская кривая задана уравнением y =  (x),
(x),  , то из пункта 1 получаем:
, то из пункта 1 получаем:

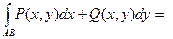

Вывод. Таким образом, исходя из уравнений (или уравнения) линии АВ, преобразуем подынтегральное выражение к одной переменной, значения которой в начале и в конце дуги АВ будут пределами определенного интеграла.
Пример 9.
Вычислить криволинейный интеграл  вдоль дуги параболы y=3x2 от точки А(1,3) до точки О(0,0).
вдоль дуги параболы y=3x2 от точки А(1,3) до точки О(0,0).
Решение:
Так как кривая задана уравнением y= φ(x) и при перемещении от точки А до точки В переменная х изменяется от хА до хВ , то криволинейный интеграл II рода сводится к определенному интегралу по формуле
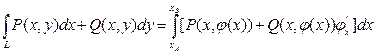
В нашем случае y=3x2, y’=6x, x изменяется от 1 до 0. Поэтому
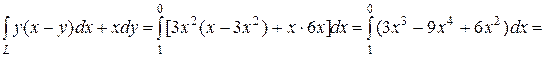
 .
.
Пример 10.
Вычислить криволинейный интеграл  вдоль дуги L окружности x=cost, y=sint
вдоль дуги L окружности x=cost, y=sint  .
.
Решение
Так как кривая задана параметрически x=x(t), y=y(t), ( 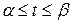 ), то криволинейный интеграл II рода сводится к определенному интегралу по формуле
), то криволинейный интеграл II рода сводится к определенному интегралу по формуле
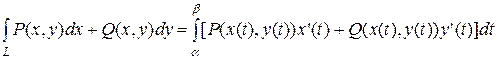 .
.
Найдем дифференциалы dx=(cost)’dt=-sintdt
dy=(sint)’dt= cost dt
Тогда

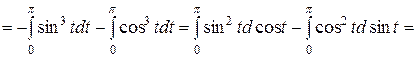

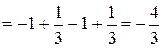 .
.
Криволинейный интеграл первого рода
Рассмотрим в плоскости Оху кривую АВ длины l . Пусть  - непрерывная в точках дуги АВ функция. Разобьем АВ произвольным образом на n частей с длинами
- непрерывная в точках дуги АВ функция. Разобьем АВ произвольным образом на n частей с длинами  . Выберем на каждой из них произвольным образом по точке Mi , найдем значения функции в этих точках и составим сумму вида
. Выберем на каждой из них произвольным образом по точке Mi , найдем значения функции в этих точках и составим сумму вида 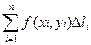
 (интегральную сумму).
(интегральную сумму).
Если существует предел этой суммы при  и не зависит от способа разбиения области на элементарные части, от выбора точек Mi , то он называется криволинейным интегралом I рода или по длине дуги.
и не зависит от способа разбиения области на элементарные части, от выбора точек Mi , то он называется криволинейным интегралом I рода или по длине дуги.

Вычисление криволинейного интеграла I рода
1. Если линия задана параметрическими уравнениями x=x(t), y=y(t), ( 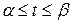 ), то криволинейный интеграл I рода сводится к определенному интегралу по формуле
), то криволинейный интеграл I рода сводится к определенному интегралу по формуле
 .
.
2. Если линия задана уравнением y=y(x), 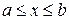 , то справедлива формула
, то справедлива формула
 .
.
Замечание.
Анализируя определения двойного, тройного, криволинейных интегралов, замечаем общность их конструкции. Сделаем общую схему их определения
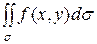 | 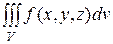 |  | 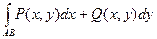 |
| 1. Выбираем точку | |||
 | 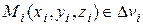 |  |  |
| 2. Составляем произведение | |||
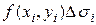 | 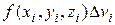 |  |  |
| 3. Составляем интегральную сумму | |||
 | 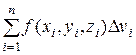 | 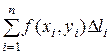 |  |
4. Переходим к пределу при 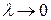 | |||
 |  |  | 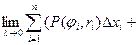  |
Приложения криволинейных интегралов
1. Длина дуги кривой  .
.
2. Масса материальной кривой с  - линейной плоскостью
- линейной плоскостью
 .
.
3. Работа силы  при перемещении материальной точки вдоль дуги кривой L:
при перемещении материальной точки вдоль дуги кривой L:
 .
.
4. Площадь фигуры, лежащей в плоскости Оху и ограниченной замкнутой линией L:
 или
или 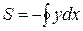 или
или 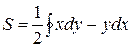 ,
,
где  - интеграл по замкнутому контуру L.
- интеграл по замкнутому контуру L.
5. Координаты центра тяжести дуги с линейной плотностью 
 ;
; 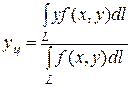 .
.
Пример 11.
Вычислить криволинейный интеграл 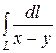 , где L – отрезок прямой, заключенный между точками А(0,-4) и В(2,0)
, где L – отрезок прямой, заключенный между точками А(0,-4) и В(2,0)
Решение
Уравнение прямой, соединяющей точки А и В :
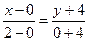 ,
, 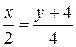 ,
,  ,
, 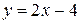
Так как кривая L задана уравнением, то криволинейный интеграл I рода, взятый по этой кривой, сводится к определенному интегралу по формуле

Найдем 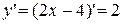 .
.
Значит

 .
.
Пример 12.
Вычислить криволинейный интеграл 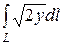 ,
,
где L – первая арка циклоиды x=a(t-sint)
y=a(1-cost)  .
.
Решение
Так как кривая задана параметрическими уравнениями, то криволинейный интеграл в этом случае сводим к определенному интегралу по формуле

Вычисляя дифференциалы
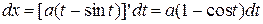 ,
,  ,
,
находим дифференциал дуги
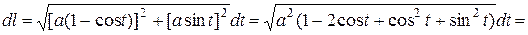
 .
.
Тогда

 .
.
Пример 13.
Вычислить криволинейный интеграл  взятый вдоль пространственной кривой L - части винтовой линии
взятый вдоль пространственной кривой L - части винтовой линии
x=4cost, y=4sint, z=3t  .
.
Решение
В этом случае криволинейный интеграл сводится к определенному по формуле
 .
.
Вычисляя дифференциалы
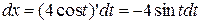 ;
; 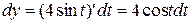 ;
; 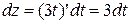 .
.
получаем дифференциал дуги
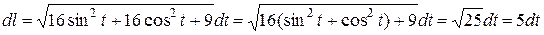 .
.
Тогда
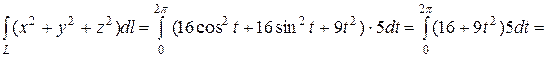
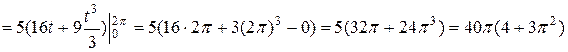 .
.
Пример 14.
При помощи криволинейного интеграла найти длину дуги кривой
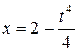 ,
, 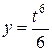 между точками пересечения ее с осями координат.
между точками пересечения ее с осями координат.
Решение
Для этого воспользуемся формулой  .
.
Найдем точки пресечения кривой с осями координат:
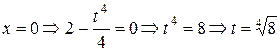
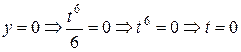
Таким образом, t изменяется от 0 до 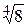


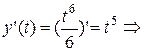



Пример 15.
Пользуясь криволинейным интегралом, найти площадь, ограниченную кривой
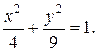
Решение
Воспользуемся формулой для вычисления площади фигуры, расположенной в плоскости хОу и ограниченной замкнутой линией L:

Данная кривая
 - это эллипс с полуосями a=2, b=3.
- это эллипс с полуосями a=2, b=3.
Переходя к параметрическим уравнениям эллипса
x=2cost, y=3sint,  ,
,
преобразуем криволинейный интеграл к определенному так:
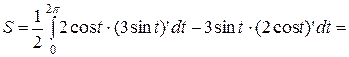
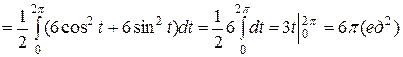 .
.
Пример 16.
Найти массу дуги кривой x=8t, y=4t2, (  ),
),
если плотность в каждой точке кривой пропорциональна корню квадратному из ординаты этой точки (коэффициент пропорциональности к=1/2).
Решение
Воспользуемся в этом случае формулой
 , где
, где  - плотность. В нашем случае
- плотность. В нашем случае 
Найдем
 ,
, 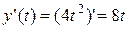 .
.
Тогда


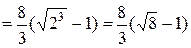 (ед).
(ед).
Пример 17.
Вычислить работу, совершаемую силой 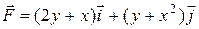 при перемещении материальной точки по дуге кривой
при перемещении материальной точки по дуге кривой  от точки О(0,0) до точки А(2,10).
от точки О(0,0) до точки А(2,10).
Решение
Воспользуемся формулой
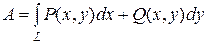 .
.
Подставляем данные задачи в эту формулу
 .
.
Найдем
 .
.
Тогда

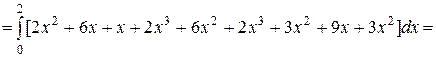
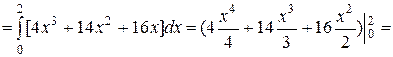
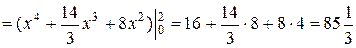 (ед).
(ед).
Индивидуальные задания для самостоятельной работы.
I. Изменить порядок интегрирования в двойном интеграле. Область интегрирования изобразить на чертеже.
1.1. 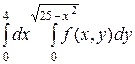
1.2. 
1.3. 
1.4. 
1.5. 
1.6. 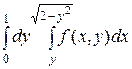
1.7. 
1.8. 
1.9. 
1.10. 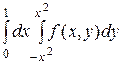
1.11. 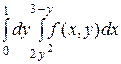
1.12. 
1.13. 
1.14. 
1.15. 
1.16. 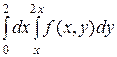
1.17. 
1.18. 
1.19. 
1.20. 
II. Пользуясь двойным интегралом, найти площадь фигуры, ограниченной линиями. Сделать чертеж.
2.1. y = x, x = 2, xy = 1
2.2. xy = 6, x+y = 7
2.3. y = -x2+4x-1, y = -x-1
2.4. y = x2+2x, x-y = -2
2.5. y = x, y = 2x, x+y = 6
2.6. y2 = x, x+y = 2
2.7. y = x2, y = 4-x2
2.8. 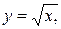
 x = 4
x = 4
2.9. 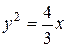 ,
, 
2.10. x = y2, 4x-6y+2 = 0
2.11. 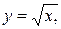
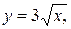 x = 9
x = 9
2.12. y2 = 2x+1, y = x-1
2.13. y = x2, x+y = 2, x = 2
2.14. y = x2, y = 3-2x
2.15. y = 2x-2, x+y = 7, y = 0, y = 2
2.16. y-x = 0, 2x-y = 6, y = 0
2.17. 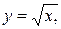 x+y = 2, y = 0
x+y = 2, y = 0
2.18. y = x2, y = 2x
2.19. 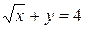 , x = 0, y = 0
, x = 0, y = 0
2.20. x = y2, y = x3
III. С помощью тройного интеграла вычислить объем тела, ограниченного данными поверхностями. Область интегрирования изобразить на чертеже.
3.1. z = 4-y2, z = y2+2, x = -1, x = 2
3.2. z = x2-y2, z = 0, x = 3
3.3. z = x2+y2, z = x2+2y2, y = x, y = 2x, x = 1
3.4. z = x, z = 0, x2+y2 = 4, 
3.5. z = y-x2, 4 x2 = y, y = 1, z = 0
3.6. z = x2+y2+1, x = 2, y = 3, x = 0, y = 0, z = 0
3.7. z = x2+y2, x+y = 1, x = 0, y = 0, z = 0
3.8. z = 2x2+y2, x+y = 2, x = 0, y = 0, z = 0
3.9. z = x2+y2, y = x2, y = 1, z = 0
3.10. z = 4-x2,  , x = 0, y = 0, z = 0
, x = 0, y = 0, z = 0
3.11 z = x2 + y2, y = 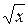 , x + y =2, z = 0, x =0
, x + y =2, z = 0, x =0
3.12 z = 9-y2, 3x+4y = 12, x = 0, y = 0, z = 0, y 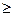 0
0
3.13 z = 4-x, y = 4x2, y = 0, z = 0
3.14 z = 4-y2,  , z = 0
, z = 0
3.15 z=x2+y2, 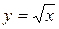 , x+y = 2, z = 0, y = 0
, x+y = 2, z = 0, y = 0
3.16. z = 3y, z = 0, x+y = 4, 
3.17 x = 15-z-y, z = 0, x = 5, y = 5
3.18. z = x2, z = 0, 2x-y = 0, x+y = 9
3.19 z = y2-x2, z = 0, y = 3
3.20 z = x2+y2+1, x = 4, y = 4, x = 0, y = 0
IV. Вычислить криволинейные интегралы вдоль заданных контуров.
4.1 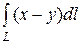 , где L – отрезок прямой от точки О(0,0) до точки B (4,3)
, где L – отрезок прямой от точки О(0,0) до точки B (4,3)
4.2 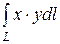 , где L – отрезок прямой от точкиA(-1,1) до точки B (1,1)
, где L – отрезок прямой от точкиA(-1,1) до точки B (1,1)
4.3 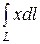 , где L – дуга параболы y = x2 от A(-1,1) до B(1,1)
, где L – дуга параболы y = x2 от A(-1,1) до B(1,1)
4.4  , где L – отрезок прямой от A(1,2) до B(2,4)
, где L – отрезок прямой от A(1,2) до B(2,4)
4.5  , где L – отрезок прямой от A(0.-2) до B(4,0)
, где L – отрезок прямой от A(0.-2) до B(4,0)
4.6 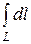 , где L – дуга циклоиды
, где L – дуга циклоиды 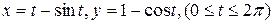
4.7  , где L – отрезок прямой, соединяющей точки M(2,0) и N(4,2)
, где L – отрезок прямой, соединяющей точки M(2,0) и N(4,2)
4.8  , где L – отрезок прямой, соединяющей точки O(0,0) и A(4,3)
, где L – отрезок прямой, соединяющей точки O(0,0) и A(4,3)
4.9 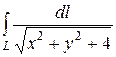 , где L – отрезок прямой, соединяющей точки O(0,0) и A(1,2)
, где L – отрезок прямой, соединяющей точки O(0,0) и A(1,2)
4.10  , где L – дуга кривой
, где L – дуга кривой 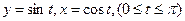
4.11  , где L – окружность x2 + y2 = 4
, где L – окружность x2 + y2 = 4
4.12  , где L – отрезок прямой от точки A(0,0) до B(1,2)
, где L – отрезок прямой от точки A(0,0) до B(1,2)
4.13  , где L – отрезок прямой от точки M(0,1) до B(2,3)
, где L – отрезок прямой от точки M(0,1) до B(2,3)
4.14  , где L - отрезок прямой y =
, где L - отрезок прямой y =  x от точки O(0,0) до B(2,1)
x от точки O(0,0) до B(2,1)
