Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса

Моменты инерции данного тела относи­тельно разных осей будут, вообще говоря, разными. Покажем, как зная момент инерции относительно какой-нибудь одной оси, проведен­ной в теле, найти момент инерции от­носительно любой другой оси, ей па­раллельной.

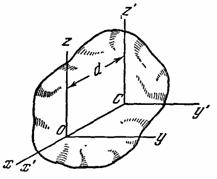
Рис.35

Проведем через центр масс С тела произвольные оси Cx'y'z', а через лю­бую точку О на оси Сх' - оси Oxyz, такие, что ОyСy', OzCz' (рис. 35). Расстояние между осями Cz' и Оz обозначим через d. Тогда

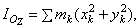
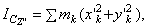
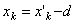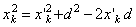но, как видно из рисунка, для любой точки тела или , а 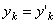. Подставляя эти значения 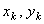, в выражение для 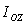и вынося общие множители d ² и 2d за скобки, получим

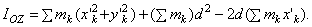
В правой части равенства первая сумма равна I_cz', а вторая - массе тела М. Найдем значение третьей суммы. На основании фор­мул для координат центра масс 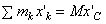.Так как в на­шем случае точка С является началом координат, то x_C = 0 и, сле­довательно, 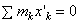. Окончательно получаем:

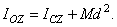
Формула выражает следующую теорему Гюйгенса:

Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

Дифференциальные уравнения движения системы

Рас­смотрим систему, состоящую из п материальных точек. Выделим какую-нибудь точку системы с массой 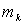. Обозначим равнодейству­ющую всех приложенных к точке внешних сил (и активных и реак­ций связей) через 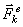, а равнодействующую всех внутренних сил - через 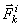. Если точка имеет при этом ускорение 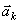, то по основному закону динамики

.

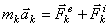Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

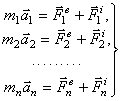
Эти уравнения, из которых можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме. Уравнения являются дифференциальными, так как 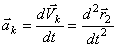; входящие в правые части уравнений силы будут в общем случае зависеть от времени, координат точек системы и их скоростей.

Проектируя на какие-нибудь координатные оси, мы можем получить дифференциальные уравнения движения системы в проекциях на эти оси.

Полное решение основной задачи динамики для системы состояло бы в том, чтобы, зная заданные силы, проинтегрировать соответ­ствующие дифференциальные уравнения и определить таким путем закон движения каждой из точек системы в отдельности.

Однако такой путь решения обычно не применяется по двум причинам. Во-первых, этот путь слишком сложен и почти всегда связан с непреодолимыми математическими трудностями. Во-вторых, в большинстве случаев при решении задач механики бывает доста­точно знать некоторые суммарные характеристики движения системы в целом, а не движение каждой из ее точек в отдельности. Эти суммарные характеристики определяются с помощью общих теорем динамики системы, к изучению которых мы и перейдем.

Основная роль уравнений состоит в том, что они, или след­ствия из них, являются исходными для получения соответствующих общих теорем.

Общие теоремы динамики механической системы: теоремы о движении центра масс механической системы и об изменении количества движения, теоремы об изменении кинетического момента и кинетической энергии, -являются следствием основного уравнения динамики. Данные теоремы рассматривают не движение отдельных точек и тел, входящих в механическую систему, а некоторые интегральные характеристики, такие как движение центра масс механической системы, ее количество движения, кинетический момент и кинетическую энергию. В результате из рассмотрения исключаются неизвестные внутренние силы, а в ряде случаев и реакции связей, что существенно упрощает решения задачи.