Задачі для самостійного розв’язування
ТЕМА 5
НЕІНЕРЦІАЛЬНІ СИСТЕМИ ВІДЛІКУ
Основні поняття і співвідношення
Другий закон Ньютона в неінерціальних системах відліку має вигляд:
 ,
,
де  - сума всіх сил, що діють на дане тіло з боку інших тіл,
- сума всіх сил, що діють на дане тіло з боку інших тіл,  - сила інерції,
- сила інерції,  - прискорення тіла в неінерціальній системі відліку.
- прискорення тіла в неінерціальній системі відліку.
В системах відліку, що рухаються поступально  , де
, де  - прискорення, з яким рухається неінерціальна система відліку.
- прискорення, з яким рухається неінерціальна система відліку.
В системах відліку, що обертаються діють :
Відцентрова сила інерції: 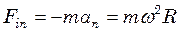 , та сила Коріоліса
, та сила Коріоліса  .
.
Методичні вказівки до розв’язування задач
В задачах, в яких розглядаються фізичні процеси, що відбуваються всередині тіла, що рухається прискорено (вагоні, ліфті і таке інше), розв’язок, який ґрунтується на застосуванні другого закону Ньютона, спрощується, якщо розглядати явище в неінерційній системі відліку, зв’язаної з тілом, що рухається прискорено. Відповідно двом рухам тіла – поступальному і обертальному – застосовують неінерціальні системи відліку, що рухаються поступально і обертально. В неінерціальних системах відліку, що рухаються поступально, другий закон Ньютона виражається рівнянням  (1) , де
(1) , де  - сума всіх сил, що діють на дане тіло з боку інших тіл,
- сума всіх сил, що діють на дане тіло з боку інших тіл,  - сила інерції,
- сила інерції,  - прискорення тіла в неінерціальній системі відліку. Це ж рівняння можна застосовувати і в системах відліку, що обертаються при умові, що матеріальна точка (частинка) в цій системі знаходиться в стані спокою. Тоді у виразі (1)
- прискорення тіла в неінерціальній системі відліку. Це ж рівняння можна застосовувати і в системах відліку, що обертаються при умові, що матеріальна точка (частинка) в цій системі знаходиться в стані спокою. Тоді у виразі (1)  ,
,  - доцентрове прискорення тієї точки системи відліку, що обертається, в якій знаходиться дана частинка. Величину
- доцентрове прискорення тієї точки системи відліку, що обертається, в якій знаходиться дана частинка. Величину  називають відцентровою силою інерції.
називають відцентровою силою інерції.
Сила інерції, що входить у рівняння (1) існує тільки в неінерціальній системі відліку і для неї не можна вказати тих конкретних тіл, з боку яких вона діє.
Приклади розв’язування задач.
I. Неінерціальні системи координат, що рухаються прямолінійно
Розв’язок: Застосовуються рівняння руху.
II. Неінерціальна система координат, що рухається зі сталою кутовою швидкістю.
Розв’язок: Застосовуються рівняння руху.
Перший тип задач.
 |
| Рис. 5.1 |
Приклад 5.1. Тіло масою  , що знаходиться на вершині похилої площини, утримується силою тертя. За який час тіло спуститься по похилій площині, якщо вона стане рухатись в горизонтальному напрямі з прискоренням
, що знаходиться на вершині похилої площини, утримується силою тертя. За який час тіло спуститься по похилій площині, якщо вона стане рухатись в горизонтальному напрямі з прискоренням  =1,00м/с2. Довжина площини
=1,00м/с2. Довжина площини  =1,00м, кут нахилу до горизонту
=1,00м, кут нахилу до горизонту  =300, коефіцієнт тертя між тілом і площиною
=300, коефіцієнт тертя між тілом і площиною  =0,60.
=0,60.
Розв’язок.Виберемо систему відліку, пов’язану з похилою площиною. Поки площина перебуває в стані спокою, на тіло діють три сили: сила тяжіння  , сила нормального тиску
, сила нормального тиску  опори і сила тертя спокою
опори і сила тертя спокою 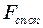 , які зрівноважують одна одну. Як тільки починається прискорений рух площини і «прив’язана» до неї система відліку стане неінерціальною, з’явиться четверта сила, що діє не тіло, - сила інерції
, які зрівноважують одна одну. Як тільки починається прискорений рух площини і «прив’язана» до неї система відліку стане неінерціальною, з’явиться четверта сила, що діє не тіло, - сила інерції  . Рівновага порушиться і тіло почне ковзати вниз по похилій площині з прискоренням
. Рівновага порушиться і тіло почне ковзати вниз по похилій площині з прискоренням  . Оскільки шуканий час визначається відомою формулою шляху рівноприскореного руху без початкової швидкості:
. Оскільки шуканий час визначається відомою формулою шляху рівноприскореного руху без початкової швидкості:
 , (1)
, (1)
то необхідно знайти прискорення  . Для цього запишемо другий закон Ньютона в неінерціальній системі відліку:
. Для цього запишемо другий закон Ньютона в неінерціальній системі відліку:
 . (2)
. (2)
Виберемо осі проекцій, як показано на рисунку. Проектуючи всі вектори, що входять в рівняння (2), на осі  і
і 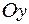 , одержимо відповідно два скалярних рівняння:
, одержимо відповідно два скалярних рівняння:
 (3)
(3)
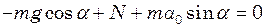 (4)
(4)
Розв’язавши системі (3),(4) з урахуванням  , знайдемо прискорення.
, знайдемо прискорення.
Тепер за формулою (1) маємо:
 .
.
Підставивши числові значення величин, знайдемо:

Приклад 5.2. Посудина з рідиною обертається навколо вертикальної осі зі сталою кутовою швидкістю  . Визначити форму поверхні рідини.
. Визначити форму поверхні рідини.
Розв’язок. Кожна точка посудини з рідиною, що обертається має прискорення, що напрямлене до осі обертання, яке рівне 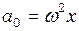 , де
, де  - відстань точки від осі обертання. Розглянемо явище в неінерціальній системі відліку, прив’язаної до посудини, що обертається. В ній рідина буде нерухомою. Розв’яжемо задачу двома способами, що відповідають двом методам пояснення поведінки тіла в неінерціальній системі відліку:
- відстань точки від осі обертання. Розглянемо явище в неінерціальній системі відліку, прив’язаної до посудини, що обертається. В ній рідина буде нерухомою. Розв’яжемо задачу двома способами, що відповідають двом методам пояснення поведінки тіла в неінерціальній системі відліку:
 |
| Рис. 5.2 а |
1 спосіб. На частинку рідини масою  , що знаходиться на поверхні на відстані
, що знаходиться на поверхні на відстані  від осі обертання, діють три сили, рис. 5.2 а
від осі обертання, діють три сили, рис. 5.2 а
1) сила тяжіння  ;
;
2) відцентрова сила інерції  ; сила реакції
; сила реакції 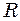 сусідніх частинок рідини.
сусідніх частинок рідини.
Рівнодійна зовнішніх сил, що діють на частинку  рідини в стані спокою, повинна бути напрямлена по нормалі до поверхні рідини в даній точці (тут зовнішніми є сили
рідини в стані спокою, повинна бути напрямлена по нормалі до поверхні рідини в даній точці (тут зовнішніми є сили  і
і  , а сила
, а сила  - їх рівнодійна). Інакше існувала б напрямлена по дотичній
- їх рівнодійна). Інакше існувала б напрямлена по дотичній  складова сили
складова сили  , яка викликала б ковзання частинки по поверхні рідини.
, яка викликала б ковзання частинки по поверхні рідини.
Звідси можна знайти кут  нахилу дотичної
нахилу дотичної  до лінії горизонту (осі
до лінії горизонту (осі  ). Як видно з рисунка:
). Як видно з рисунка:
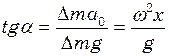 .
.
Враховуючи, що  , отримаємо диференціальне рівняння кривої, обертання якої навколо осі
, отримаємо диференціальне рівняння кривої, обертання якої навколо осі  утворює поверхню рідини:
утворює поверхню рідини:
 ,
,
Звідки
 (1)
(1)
Очевидно, при заданому виборі осі  стала
стала  =0
=0
З формули (1) випливає, що крива – парабола. Отже, поверхня рідини є параболоїдом обертання.
 |
| Рис. 5.2 б |
2 спосіб. Не будемо вводити сили інерції, але врахуємо, що при обертанні посудини в зв’язаній з нею системі відліку змінюється поле тяжіння. При цьому нове прискорення сили тяжіння  виражається через старе прискорення
виражається через старе прискорення  співвідношенням
співвідношенням  .
.
Виберемо точку  поверхні рідини, рис. 5.2 б, розташовану на відстані
поверхні рідини, рис. 5.2 б, розташовану на відстані  від осі обертання. Нехай вектори
від осі обертання. Нехай вектори  і
і  утворюють в цій точці кут
утворюють в цій точці кут  . Оскільки поверхня рідини в стані спокою завжди нормальна до напрямку сили тяжіння, то, як видно з рисунка, між дотичною
. Оскільки поверхня рідини в стані спокою завжди нормальна до напрямку сили тяжіння, то, як видно з рисунка, між дотичною  і лінією горизонту (віссю
і лінією горизонту (віссю  ) також буде кут
) також буде кут  , при цьому
, при цьому
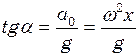 .
.
Подальший хід розв’язку співпадає з тим, що отримано в першому способі.
 |
| Рис. 5.3 |
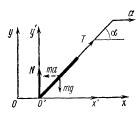
Приклад 5.3.Однорідний круглий циліндр з намотаними на ньому двома тонкими нитками із закріпленими верхніми кінцями опускається вниз і обертається навколо своєї осі симетрії, рис. 5.3. Не враховуючи сил тертя, визначити прискорення  точок, що лежать на осі циліндра.
точок, що лежать на осі циліндра.
Розв’язок.В неінерціальній системі координат  до сил взаємодії
до сил взаємодії  і
і  необхідно додати силу інерції -
необхідно додати силу інерції -  . Для рівнянь руху в цьому випадку маємо:
. Для рівнянь руху в цьому випадку маємо:
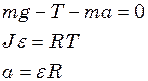
де  - вага циліндра,
- вага циліндра,  - натяг двох ниток,
- натяг двох ниток, 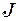 - момент інерції циліндра відносно його осі,
- момент інерції циліндра відносно його осі,  - кутове прискорення,
- кутове прискорення, 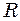 - радіус циліндра. При
- радіус циліндра. При  ці рівняння дають:
ці рівняння дають:
 .
.
 |
| Рис. 5.4 |
Приклад 5.4.Однорідний стержень підвішений на нитці і спирається кінцем на абсолютно гладку площину, рис. 5.4. Точка підвісу починає рухатися горизонтально з прискоренням  , при якому вісь стержня і нитка утворюють пряму лінію з кутом
, при якому вісь стержня і нитка утворюють пряму лінію з кутом  до горизонту. Визначити це прискорення і величину реакції
до горизонту. Визначити це прискорення і величину реакції  при русі.
при русі.
Розв’язок.В неінерціальній системі відліку  до звичайних сил взаємодії (натяг нитки
до звичайних сил взаємодії (натяг нитки  , сила тяжіння
, сила тяжіння  і
і  ) необхідно додати силу інерції -
) необхідно додати силу інерції -  .
.
Сума моментів сил відносно точки  дає:
дає:
 ,
,
де  - половина довжини стержня.
- половина довжини стержня.
Для величини шуканого прискорення одержимо:

Рівняння моментів відносно центра мас стержня дає:
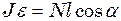 ,
,
де 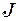 - момент інерції стержня відносно точки центра мас,
- момент інерції стержня відносно точки центра мас,  - кутове прискорення обертання стержня. Оскільки
- кутове прискорення обертання стержня. Оскільки  =0, то при
=0, то при  , одержимо, що
, одержимо, що  =0.
=0.
Для визначення прискорення  можна скористатися рівняннями:
можна скористатися рівняннями:
 ,
,
де  - маса стержня,
- маса стержня,  - прискорення вільного падіння. Ці рівняння дають:
- прискорення вільного падіння. Ці рівняння дають:
 .
.
 |
| Рис. 5.5 |
Приклад 5.5. Математичний маятник з довжиною нитки  і масою кульки
і масою кульки  підвішений на дошці, що вільно падає (з прискоренням
підвішений на дошці, що вільно падає (з прискоренням  ). Як буде рухатись маятник (кулька) відносно дошки, якщо вона починає свій рух в момент, коли швидкість кульки не дорівнює нулю?
). Як буде рухатись маятник (кулька) відносно дошки, якщо вона починає свій рух в момент, коли швидкість кульки не дорівнює нулю?
Розв’язок.В неінерціальній системі координат  крім сили тяжіння
крім сили тяжіння  і натягу нитки
і натягу нитки  необхідно врахувати силу інерції -
необхідно врахувати силу інерції -  . Сума моментів всіх трьох сил відносно точки
. Сума моментів всіх трьох сил відносно точки  дорівнює нулю. Для рівняння обертового руху маятника це дає:
дорівнює нулю. Для рівняння обертового руху маятника це дає:
 ,
,
де  - момент інерції маятника,
- момент інерції маятника,  - кут відхилення маятника,
- кут відхилення маятника, 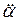 - його кутове прискорення. З цього рівняння випливає, що
- його кутове прискорення. З цього рівняння випливає, що 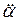 =0. Маятник буде обертатися зі сталою кутовою швидкістю:
=0. Маятник буде обертатися зі сталою кутовою швидкістю:
 .
.
В інерціальній системі  для координат маятника
для координат маятника

Для рівнянь руху

Для компонентів прискорення отримаємо:
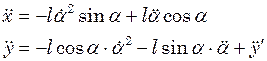
Вважаючи, що 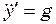 ,
,  ,
, 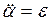 , з рівнянь руху отримаємо:
, з рівнянь руху отримаємо:
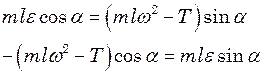
Ці два рівняння сумісні, якщо:
 і
і  .
.
Перше рівняння дає величину сили  , прикладеної до кульки. Друге призводить до сталої кутової швидкості обертання маятника:
, прикладеної до кульки. Друге призводить до сталої кутової швидкості обертання маятника:
 .
.
Другий тип задач.
Приклад 5.6. Вигнутий стержень ОА, рис. 5.6, може обертатися навколо вертикальної осі 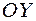 . На стержні є кільце С, яке може вільно, без тертя переміщуватися по стержню. Визначити рівняння (форму)
. На стержні є кільце С, яке може вільно, без тертя переміщуватися по стержню. Визначити рівняння (форму) 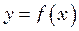 стержня, при якому кільце при будь-якій кутовій швидкості
стержня, при якому кільце при будь-якій кутовій швидкості  обертання стержня не буде по ньому переміщатися.
обертання стержня не буде по ньому переміщатися.
 |
| Рис. 5.6 |
Розв’язок. 1. В неінерціальній системі координат  , що обертається зі сталою кутовою швидкістю
, що обертається зі сталою кутовою швидкістю  , до сили тяжіння
, до сили тяжіння  і реакції опори
і реакції опори  слід додати відцентрову силу інерції
слід додати відцентрову силу інерції  , де
, де  - маса кільця,
- маса кільця, 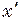 - відстань кільця від осі обертання (вісь
- відстань кільця від осі обертання (вісь  ).
).
Щоб кільце перебувало в стані спокою при будь-якій кутовій швидкості обертання стержня, необхідно, щоб сума всіх сил вздовж напрямку можливого переміщення була рівна нулю, тобто:
 ,
,
де  - прискорення сили тяжіння,
- прискорення сили тяжіння,  - кут між дотичною до лінії стержня в точці, де знаходиться кільце, і віссю
- кут між дотичною до лінії стержня в точці, де знаходиться кільце, і віссю  . З цього рівняння отримуємо:
. З цього рівняння отримуємо:
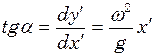 .
.
Інтегрування дає рівняння параболи:
 .
.
2. В інерціальній системі координат  доцентровою силою буде векторна сума сил тяжіння і реакція опори кільця. Маємо:
доцентровою силою буде векторна сума сил тяжіння і реакція опори кільця. Маємо:
 .
.
Інтегрування дає, як і в попередньому випадку, рівняння параболи:
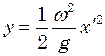
 |
| Рис. 5.7 |
Приклад 5.7. Тонкий однорідний стержень довжиною  , рис. 5.7, і масою
, рис. 5.7, і масою  обертається за інерцією зі сталою кутовою швидкістю
обертається за інерцією зі сталою кутовою швидкістю  навколо вертикальної осі, що проходить через його верхній кінець О. Визначити кут
навколо вертикальної осі, що проходить через його верхній кінець О. Визначити кут  стійкого обертання стержня.
стійкого обертання стержня.
Розв’язок.В неінерціальній системі координат, що обертається разом зі стержнем, до кожного елементу довжини стержня  буде прикладена елементарна відцентрова сила інерції
буде прикладена елементарна відцентрова сила інерції
 ,
,
де  - площа поперечного перерізу стержня,
- площа поперечного перерізу стержня,  - його густина,
- його густина,  - відстань елемента стержня від осі обертання.
- відстань елемента стержня від осі обертання.
Момент цієї сили відносно точки О буде:
 ,
,
де  - відстань елемента маси від осі обертання.
- відстань елемента маси від осі обертання.
Сума моментів цих сил буде:
 .
.
В розглядуваній системі координат стержень знаходиться в стані спокою – момент сили інерції повинен дорівнювати моменту сили тяжіння  . Рівність моментів сил дає:
. Рівність моментів сил дає:
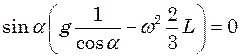 .
.
Це рівняння для шуканої величини кута дає два розв’язки:
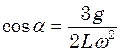 ,
, 
Розв’язок  не відповідає реальним умовам задачі (нестійкий рух).
не відповідає реальним умовам задачі (нестійкий рух).
В інерціальній системі відліку обертання стержня можна розглядати як рух конічного фізичного маятника. Його рух в цьому випадку можна звести до руху також конічного, але математичного маятника. Періоди коливань математичного маятника і стержня повинні дорівнювати:
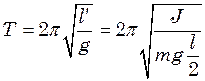
де  - довжина математичного маятника,
- довжина математичного маятника, 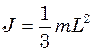 - момент інерції стержня відносно точки О.
- момент інерції стержня відносно точки О.
Для величини  (відстань від точки прикладання сумарної доцентрової сили, що діє на стержень, до точки О) одержимо:
(відстань від точки прикладання сумарної доцентрової сили, що діє на стержень, до точки О) одержимо:
 .
.
Для радіуса обертання цієї точки маємо:
 .
.
Рівняння руху стержня буде:
 .
.
або, як і раніше:
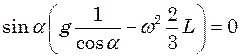 .
.
Приклад 5.8. Обертання Землі навколо своєї осі викликає відхилення поверхні води в ріці від її горизонтального положення. Визначити, біля якого берега і на яку величину  рівень води буде вищий. Ріка тече в північній півкулі з півночі на південь. Ширина річки
рівень води буде вищий. Ріка тече в північній півкулі з півночі на південь. Ширина річки  , швидкість течії
, швидкість течії  , широта місцевості
, широта місцевості 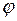 , кутова швидкість обертання Землі
, кутова швидкість обертання Землі  . Відцентровою силою інерції знехтувати.
. Відцентровою силою інерції знехтувати.
Розв’язок.1.В неінерціальній системі відліку, пов’язаною із Землею, крім сили тяжіння  необхідно врахувати силу інерції Коріоліса:
необхідно врахувати силу інерції Коріоліса:
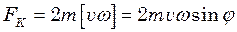
Рівняння руху для частинки води буде:
 ,
,
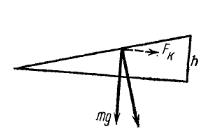 |
| Рис. 5.8 |
де  - маса частинки,
- маса частинки,  - прискорення частинки,
- прискорення частинки,  - прискорення сили тяжіння. Результуюча цих двох сил буде перпендикулярна до лінії рівня води. З рис. 5.8 видно, що
- прискорення сили тяжіння. Результуюча цих двох сил буде перпендикулярна до лінії рівня води. З рис. 5.8 видно, що
 .
.
Рівень води буде вищим біля правого берега річки на величину, яка визначається з останнього рівняння.
Маємо:
 .
.
2. В інерціальній системі відліку рух частинок води слід розглядати як складний, що складається одночасно з відносного і переносного рухів. Першим є рух по меридіану зі швидкістю  . Переносний рух зумовлений обертанням Землі з кутовою швидкістю
. Переносний рух зумовлений обертанням Землі з кутовою швидкістю  . Різниця рівнів води пояснюється впливом правого берега ріки.
. Різниця рівнів води пояснюється впливом правого берега ріки.
Для рівняння руху в цьому випадку маємо

де 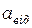 - прискорення відносного руху,
- прискорення відносного руху,  - прискорення Коріоліса.
- прискорення Коріоліса.
 |
| Рис. 5.9 |
Приклад 5.9. На Землі, що обертається навколо своєї осі з кутовою швидкістю  по екватору зі сходу на захід, з відносною швидкістю
по екватору зі сходу на захід, з відносною швидкістю  рухається поїзд маси
рухається поїзд маси  . Не враховуючи сил тертя, вважаючи поїзд єдиним твердим тілом, визначити силу, що діє на поїзд з боку рейок (реакцію зв’язку)
. Не враховуючи сил тертя, вважаючи поїзд єдиним твердим тілом, визначити силу, що діє на поїзд з боку рейок (реакцію зв’язку)  .
.
Розв’язок. 1. В неінерціальній системі координат кім звичай них сил взаємодії, а саме сили тяжіння поїзда  і реакції зв’язку
і реакції зв’язку  , необхідно враховувати відцентрову силу інерції
, необхідно враховувати відцентрову силу інерції  і силу інерції Коріоліса
і силу інерції Коріоліса 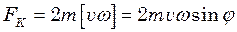 . Для рівняння руху маємо:
. Для рівняння руху маємо:
 ,
,
де 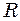 - радіус Землі.
- радіус Землі.
Для шуканої величини одержимо:

2. В інерціальній системі відліку рух слід розглядати як складний з відносною швидкістю  і переносною
і переносною  . Повне прискорення в цьому випадку буде:
. Повне прискорення в цьому випадку буде:

Для рівняння руху в цьому випадку маємо
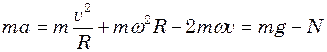
З цього рівняння, як і в попередньому випадку, одержимо:

Задачі для самостійного розв’язування
І РІВЕНЬ
5.1.1. Кулька на нитці підвішена до стелі трамвайного вагона. Вагон гальмує, і його швидкість за час  =3 с рівномірно зменшується від
=3 с рівномірно зменшується від  =18 км/год до
=18 км/год до  =6 км/год. На який кут відхилиться при цьому нитка з кулькою?
=6 км/год. На який кут відхилиться при цьому нитка з кулькою?
5.1.2. Вагон гальмує, і його швидкість зменшується за час  =3,3 с зменшується від
=3,3 с зменшується від  =47,5 км/год до
=47,5 км/год до  =30 км/год. Яким повинен бути граничний коефіцієнт тертя
=30 км/год. Яким повинен бути граничний коефіцієнт тертя  між валізою і полицею, щоб валіза при гальмуванні почала ковзати по полиці?
між валізою і полицею, щоб валіза при гальмуванні почала ковзати по полиці?
5.1.3. Диск обертається навколо вертикальної осі з частотою  =30 об/хв.. На відстані
=30 об/хв.. На відстані  =20 см від осі обертання на диску лежить тіло. Яким повинен бути коефіцієнт тертя
=20 см від осі обертання на диску лежить тіло. Яким повинен бути коефіцієнт тертя  між тілом і диском, щоб тіло не скотилося з диска.
між тілом і диском, щоб тіло не скотилося з диска.
 |
| Рис. 5.10 |
5.1.4. З якою горизонтальною силою  слід рухати похилу площину масою
слід рухати похилу площину масою  з кутом
з кутом  до горизонту, щоб тіло масою
до горизонту, щоб тіло масою  , що лежить на ній, не переміщалося відносно похилої площини? Коефіцієнт сили тертя ковзання між тілами
, що лежить на ній, не переміщалося відносно похилої площини? Коефіцієнт сили тертя ковзання між тілами  .
.
5.1.5. На клин, рис. 5.10, площина якого складає кут 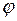 з горизонтом поклали шайбу
з горизонтом поклали шайбу 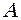 . Яке прискорення необхідно надати клину в горизонтальному напрямі, щоб шайба
. Яке прискорення необхідно надати клину в горизонтальному напрямі, щоб шайба 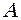 вільно падала вертикально вниз? Тертям шайби об клин знехтувати.
вільно падала вертикально вниз? Тертям шайби об клин знехтувати.
5.1.6. Суцільний циліндр скочується без ковзання з похилої площини з кутом  до горизонту. Сама похила площина опускається в ліфті з прискоренням
до горизонту. Сама похила площина опускається в ліфті з прискоренням  . Не враховуючи сил тертя кочення, визначити прискорення
. Не враховуючи сил тертя кочення, визначити прискорення  осі циліндра відносно похилої площини. Розв’язати задачу в інерціальній та неінерціальній системі координат.
осі циліндра відносно похилої площини. Розв’язати задачу в інерціальній та неінерціальній системі координат.
5.1.7. Визначити прискорення  вантажів на машині Атвуда. Блок невагомий, нитка нерозтяжна, тертя не враховувати. Маси вантажів
вантажів на машині Атвуда. Блок невагомий, нитка нерозтяжна, тертя не враховувати. Маси вантажів  і
і  (
(  ). Розв’язати задачу:
). Розв’язати задачу:
1) в неінерціальній системі координат, пов’язаній з вантажем, що опускається;
2) в неінерціальній системі координат, пов’язаній з вантажем, що піднімається. Порівняти вихідні рівняння руху.
5.1.8. Враховуючи наявність відцентрової сили інерції на Землі, що обертається навколо своєї осі, визначити зміну прискорення сили тяжіння в залежності від географічної широти 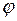 місцевості. Землю вважати сферою. Радіус Землі прийняти рівним 6400 км. Четвертим степенем кутової швидкості Землі, порівняно з її квадратом, знехтувати.
місцевості. Землю вважати сферою. Радіус Землі прийняти рівним 6400 км. Четвертим степенем кутової швидкості Землі, порівняно з її квадратом, знехтувати.
 |
| Рис. 5.11 |
5.1.9. Добове обертання Землі призводить до відхилення тіл, що падають в напрямку сходу. Визначити, на яку відстань  тіло, що вільно падає з висоти
тіло, що вільно падає з висоти  на екваторі, відхилиться біля поверхні Землі від земного радіуса, продовженого до початкового положення тіла. Вважати, що сила Коріоліса напрямлена завжди по нормалі до радіуса Землі, проведеного через початкову точку падіння тіла.
на екваторі, відхилиться біля поверхні Землі від земного радіуса, продовженого до початкового положення тіла. Вважати, що сила Коріоліса напрямлена завжди по нормалі до радіуса Землі, проведеного через початкову точку падіння тіла.
5.1.10. Прямий стержень  , нахилений під кутом
, нахилений під кутом  до горизонталі, обертається навколо вертикальної осі
до горизонталі, обертається навколо вертикальної осі 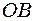 з кутовою швидкістю
з кутовою швидкістю  . По стержню може ковзати маленька втулка
. По стержню може ковзати маленька втулка 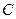 . Коефіцієнт тертя ковзання
. Коефіцієнт тертя ковзання 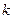 заданий кутом тертя
заданий кутом тертя 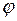 (
(  ). Визначити відстань
). Визначити відстань  від втулки до осі обертання, починаючи з якої втулка буде ковзати вниз, і відстань
від втулки до осі обертання, починаючи з якої втулка буде ковзати вниз, і відстань 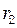 , починаючи з якої втулка буде ковзати вгору.
, починаючи з якої втулка буде ковзати вгору.
5.1.11. Кулька масою  прив’язана до мотузки довжиною
прив’язана до мотузки довжиною  , другий кінець якої закріплений нерухомо. Мотузку розкрутили до швидкості
, другий кінець якої закріплений нерухомо. Мотузку розкрутили до швидкості  , потім систему полишили саму на себе. Вважається, що сила тяжіння відсутня і можна знехтувати тертям. Який закон руху кульки?
, потім систему полишили саму на себе. Вважається, що сила тяжіння відсутня і можна знехтувати тертям. Який закон руху кульки?
5.1.12. В багажнику автомобіля знаходиться вантаж масою  =42 кг. Автомобіль, що їхав з швидкістю
=42 кг. Автомобіль, що їхав з швидкістю 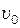 =36 км/год, різко гальмує і зупиняється на відстані
=36 км/год, різко гальмує і зупиняється на відстані  = 7 м від місця початку гальмування. Знайти силу
= 7 м від місця початку гальмування. Знайти силу  , з якою вантаж притискається до передньої стінки багажника при гальмуванні.
, з якою вантаж притискається до передньої стінки багажника при гальмуванні.
5.1.13. Камінь, прив’язаний до мотузки довжиною  =50 см, рівномірно обертається у вертикальній площині. Знайти при якій частоті обертання
=50 см, рівномірно обертається у вертикальній площині. Знайти при якій частоті обертання  мотузка розірветься, якщо відомо, що вона розривається при навантаженні, рівному десятикратній вазі каменя.
мотузка розірветься, якщо відомо, що вона розривається при навантаженні, рівному десятикратній вазі каменя.
5.1.14. Літак здійснює «мертву петлю» радіусом 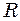 =500 м і рухається по ній з швидкістю
=500 м і рухається по ній з швидкістю  =360 км/год. З якою силою тіло пілота масою
=360 км/год. З якою силою тіло пілота масою  =70 кг буде тиснути на сидіння літака у:
=70 кг буде тиснути на сидіння літака у:
1) верхній,
2) нижній;
3) середній точках петлі?
5.1.15. Гирька масою  =0,5 кг, прив’язана до гумового шнура довжиною
=0,5 кг, прив’язана до гумового шнура довжиною  , описує в горизонтальній площині коло. Частота обертання гирьки
, описує в горизонтальній площині коло. Частота обертання гирьки  =2 об/с, кут відхилення шнура від вертикалі
=2 об/с, кут відхилення шнура від вертикалі  =300. Знайти довжину
=300. Знайти довжину  не розтягнутого шнура, якщо для його розтягу на
не розтягнутого шнура, якщо для його розтягу на  =1 см потрібна сила
=1 см потрібна сила  =6Н.
=6Н.
5.1.16. Камінь, прив’язаний до мотузки довжиною 
 , рівномірно обертається в умовах невагомості. Знайти кутову швидкість обертання каменя, при якій мотузка розірветься, якщо відомо, що вона розривається при натягу з силою
, рівномірно обертається в умовах невагомості. Знайти кутову швидкість обертання каменя, при якій мотузка розірветься, якщо відомо, що вона розривається при натягу з силою  .
.
5.1.17. Камінь масою  висить на нерухомому гумовому шнурі. Наскільки коротшим виявиться шнур, якщо відв’язати камінь, при умові, що для видовження шнура на величину
висить на нерухомому гумовому шнурі. Наскільки коротшим виявиться шнур, якщо відв’язати камінь, при умові, що для видовження шнура на величину  потрібна сила
потрібна сила  .
.
ІІ РІВЕНЬ
5.2.1. Отримати закон вільного падіння тіла на широті 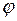 в полі тяжіння Землі, враховуючи її обертання.
в полі тяжіння Землі, враховуючи її обертання.
5.2.2. Відносно горизонтально розташованого диска, що обертається з кутовою швидкістю  , тіло, яке лежить на диску, знаходиться в стані спокою. Маса тіла дорівнює
, тіло, яке лежить на диску, знаходиться в стані спокою. Маса тіла дорівнює  , відстань від осі обертання
, відстань від осі обертання  .
.
а) Які сили діють на тіло в нерухомій системі відліку?
б) В якій системі відліку до попередніх сил додається тільки відцентрова сила інерції?
в) В якій системі відліку з’явиться ще й сила Коріоліса?
5.2.3. Яку потужність  розвиває сила Коріоліса?
розвиває сила Коріоліса?
5.2.4. Яку роботу 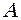 виконує над частинкою коріолісова сила при переміщенні частинки відносно обертової системи відліку з точки 1 в точку 2?
виконує над частинкою коріолісова сила при переміщенні частинки відносно обертової системи відліку з точки 1 в точку 2?
5.2.5. Рух частинки масою  =10,0 г розглядається в системі відліку, що обертається відносно інерціальної системи з кутовою швидкістю
=10,0 г розглядається в системі відліку, що обертається відносно інерціальної системи з кутовою швидкістю  =10,0 рад/с. Яку роботу виконують над частинкою сили інерції при переміщенні її з точки, що знаходиться на відстані
=10,0 рад/с. Яку роботу виконують над частинкою сили інерції при переміщенні її з точки, що знаходиться на відстані  =1,00 м від осі обертання, в точку, що знаходиться на відстані
=1,00 м від осі обертання, в точку, що знаходиться на відстані  =2,00 м?
=2,00 м?
5.2.6. Є горизонтально розташована рушниця, ствол якої співпадає з віссю вертикального циліндра. Циліндр обертається з кутовою швидкістю  , рис. 5.12.
, рис. 5.12.
 |
| Рис. 5.12 |
а) Вважаючи, що куля, яка вилетіла з рушниці, летить горизонтально зі сталою швидкістю  , знайти зміщення
, знайти зміщення  точки
точки  циліндра, в яку потрапить куля, відносно точки
циліндра, в яку потрапить куля, відносно точки 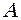 , яка знаходиться навпроти ствола в момент пострілу. Розв’язати задачу двома методами: в нерухомій системі відліку і в системі відліку, пов’язаної з циліндром.
, яка знаходиться навпроти ствола в момент пострілу. Розв’язати задачу двома методами: в нерухомій системі відліку і в системі відліку, пов’язаної з циліндром.
б) Чи залежить результат від того, обертається рушниця разом з циліндром чи нерухома?
5.2.7. На широті  =450 з рушниці, закріпленої горизонтально в площині меридіану, здійснено постріл по мішені, розташованій на відстані
=450 з рушниці, закріпленої горизонтально в площині меридіану, здійснено постріл по мішені, розташованій на відстані  =100,0 м від ствола рушниці. Центр мішені знаходиться на осі ствола рушниці. Вважаючи, що куля летить горизонтально зі сталою швидкістю
=100,0 м від ствола рушниці. Центр мішені знаходиться на осі ствола рушниці. Вважаючи, що куля летить горизонтально зі сталою швидкістю  =500м/с, визначити, на яку відстань і в який бік відхилиться куля від центра мішені, якщо постріл здійснено в напрямку:
=500м/с, визначити, на яку відстань і в який бік відхилиться куля від центра мішені, якщо постріл здійснено в напрямку:
а) на північ;
б) на південь.
5.2.8. Електровоз масою  =184·103 кг рухається вздовж меридіана зі швидкістю
=184·103 кг рухається вздовж меридіана зі швидкістю  =20,0м/с (72 км/год.) на широті
=20,0м/с (72 км/год.) на широті  =450. Визначити горизонтальну складову
=450. Визначити горизонтальну складову  сили, з якою електровоз тисне на рейки.
сили, з якою електровоз тисне на рейки.
5.2.9. Горизонтально розташований диск обертається навколо осі, що проходить через його центр, з кутовою швидкістю  . По диску рухається рівномірно на однаковій відстані від осі обертання частинка. Знайти миттєве значення:
. По диску рухається рівномірно на однаковій відстані від осі обертання частинка. Знайти миттєве значення:
а) швидкості частинки  відносно диска, при якій сила Коріоліса буде врівноважуватись відцентровою силою інерції. Виразити
відносно диска, при якій сила Коріоліса буде врівноважуватись відцентровою силою інерції. Виразити  через миттєве значення радіус-вектора
через миттєве значення радіус-вектора  , проведеного до частинки з центра диска.
, проведеного до частинки з центра диска.
б) швидкості частинки  відносно нерухомої системи відліку при тих самих умовах.
відносно нерухомої системи відліку при тих самих умовах.
5.2.10. Горизонтально розташований стержень обертається навколо нерухомої осі, що проходить через його кінець, з кутовою швидкістю  =1,00 рад/с. Відстань від осі до другого кінця стержня
=1,00 рад/с. Відстань від осі до другого кінця стержня  =1,00 м. На стержень надіта муфта масою
=1,00 м. На стержень надіта муфта масою  =0,100 кг. Муфта закріплена за допомогою нитки на відстані
=0,100 кг. Муфта закріплена за допомогою нитки на відстані 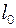 =0,100 м від осі обертання. В момент
=0,100 м від осі обертання. В момент  =0 нитку перепалюють і муфта починає ковзати по стержню практично без тертя. Знайти:
=0 нитку перепалюють і муфта починає ковзати по стержню практично без тертя. Знайти:
а) час  , за який муфта злетить зі стержня;
, за який муфта злетить зі стержня;
б) силу  , з якою стержень діє на муфту в момент
, з якою стержень діє на муфту в момент  ;
;
в) роботу 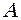 , яка виконується над муфтою за час
, яка виконується над муфтою за час  в нерухомій системі відліку.
в нерухомій системі відліку.
5.2.11. Горизонтально розташований диск обертається з кутовою швидкістю  . Вздовж радіуса диска рухається частинка масою
. Вздовж радіуса диска рухається частинка масою  , відстань якої від центра диска змінюється з часом за законом
, відстань якої від центра диска змінюється з часом за законом 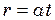 (
(  - константа). Знайти результуючий момент
- константа). Знайти результуючий момент  сил, що діють на частинку в системі відліку, пов’язаної з диском. Мається на увазі момент відносно центра диска.
сил, що діють на частинку в системі відліку, пов’язаної з диском. Мається на увазі момент відносно центра диска.
5.2.12. Є система відліку, що обертається відносно інерціальних системи навколо осі  з сталою кутовою швидкістю
з сталою кутовою швидкістю  . З точки
. З точки  , що знаходиться на осі
, що знаходиться на осі  , вилітає в перпендикулярному до осі напрямку частинка масою
, вилітає в перпендикулярному до осі напрямку частинка масою  і летить відносно інерціальної системи прямолінійно з постійною швидкістю
і летить відносно інерціальної системи прямолінійно з постійною швидкістю  . Знайти момент імпульсу
. Знайти момент імпульсу  частинки, що спостерігається в обертовій системі відліку, відносно точки
частинки, що спостерігається в обертовій системі відліку, відносно точки  . Показати, що виникнення
. Показати, що виникнення  зумовлене дією сили Коріоліса.
зумовлене дією сили Коріоліса.
