Оценка погрешностей косвенных измерений
Результат косвенного измерения находят по данным прямых измерений нескольких величин (аргументов), связанных известной функциональной зависимостью с искомым результатом.
Вначале рассмотрим простейший случай, когда искомая величина У определяется как сумма двух величин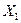 
и 
:
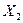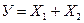(2.6)
Поскольку результаты прямых измерений величин 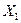и 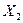(после исключения систематических погрешностей) включает в себя некоторые случайные погрешности, то формулу косвенного измерения суммы можно переписать в виде
, (2.7)
где 
, 
- среднее арифметические (или средние взвешенные), полученные при обработке результатов прямых измерений величин , ;
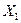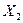- случайные погрешности;
- оценка истинного значения косвенно измеряемой величины и ее случайная погрешность.
Из уравнения (2) непосредственно вытекает справедливость двух последних равенств:
; 
,
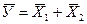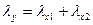т.е. оценкой истинного значения косвенно измеряемой величины должна служить сумма оценок истинных значений исходных величин, случайные погрешности которых складываются .
Математическое ожидание оценки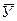 
равно сумме истинных значений величин 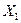, , 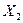и следовательно является истинным значением измеряемой величины У:
(2.8)
и ее дисперсия составляет:
Математическое ожидание произведения случайных погрешностей называется корреляционным моментом и определяет степень «тесноты» линейной независимости между погрешностями. Вместо корреляционного момента часто пользуются безразмерной величиной, называемой коэффициент корреляции:
(2.9)
Отсюда в частности следует, что коэффициент корреляции между погрешностями 
и 
средних арифметических равен коэффициенту корреляции между погрешностями результатов отдельных измерений величин , :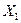
.
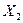С учетом коэффициента корреляции с.к.о. результата косвенных измерений, т.е. оценки истинного значения косвенно измеряемой величины будет
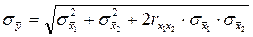. (2.10)
Если погрешности измерения величин 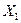, 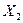не коррелированны, то выражение (2.10) упрощается:
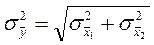(2.11)
В тех случаях, когда теоретические с.к.о. результатов прямых измерений неизвестны, определяется оценка 
с.к.о. результата косвенных измерений через оценки с.к.о.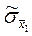 
и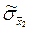 
:
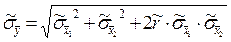. (2.12)
Оценки коэффициента корреляции 
вычисляют на основании результатов прямых измерений исходных величин:
, (2.13)
где 
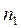- наименьшее из чисел наблюдений 
и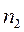 
.
При положительной корреляции, т.е. когда 
, одна из погрешностей имеет тенденцию возрастать при увеличении другой, если же корреляция отрицательна, то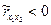 
и погрешность измерения одной величины обнаруживает тенденцию к уменьшению при увеличении погрешности измерения другой величины. Возможные значения коэффициента корреляции лежат в интервале 
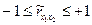. Если 
=0, то погрешности измерения не коррелированны.
О наличии корреляции удобно судить по графику, на котором в координатах 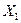, 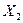изображены пары последовательно получаемых результатов измерения величин , .
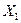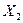На рис. 2.3 изображены случаи совместного распределения результатов измерения при положительной (рис. 2.3 а) и отрицательной (рис. 2.3 б) корреляции. Результаты измерений на рис.2.3 в не коррелированны.
а б в
Рисунок 2.3 - Случаи совместного распределения результатов измерения
Чаще всего наличия корреляции следует ожидать в тех случаях, когда обе величины измеряются одновременно однотипными средствами измерения, причем измерения внешних влияющих величин (электрических, магнитных, температурных, условий питания и прочее) одновременно заметно влияют на формирование случайных погрешностей их измерения. В некоторых случаях причиной корреляции между результатами измерений может стать сам производящий измерения, т.к. искусство и опыт наблюдателя показывают значительное влияние на результаты измерений.
В тех же случаях, когда исходные величины измеряют с помощью различных средств измерения в разное время, можно с полным правом ожидать , что результаты, если и будут коррелированны, то очень мало , и коэффициентом корреляции в выражениях (2.10) и (2.12) можно пренебречь.
Рассмотренные выражения можно использовать и в том случае, когда искомая величина является суммой m измеряемых прямыми способами величин:
. (2.14)
В этом случае в качестве наиболее достоверной оценки 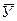принимается сумма оценок 
:
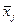. (2.15)
а с.к.о. оценки итогового результата находят по формуле:
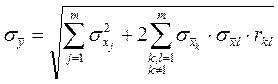(2.16)
где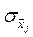 
- с.к.о. j-го слагаемого;
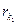- коэффициент корреляции между случайными погрешностями k-го и l-го слагаемых.
При неизвестных с.к.о. слагаемых в выражение (2.16) следует подставлять их оценки 
, а оценки коэффициентов корреляции вычисляют по формуле
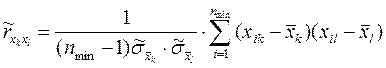, (2.17)
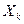где - наименьшее из чисел наблюдений 
и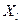 
.
Если исходные измерения независимы, то все коэффициенты корреляции равны нулю и с.к.о. оценки Y определяют с помощью более простого выражения
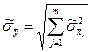(2.18)
Рассмотрим теперь общий случай, когда требуется оценить истинное значение величины У, которая связана с величинами 
, измеряемыми прямыми способами, некоторым нелинейным уравнением
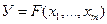(2.19)
Найдем такие оценки истинных значений 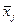измеряемых прямыми способами величин 
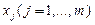которые, будучи подставлены в уравнение (2.19), давали бы оценку 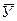истинного значения косвенно измеряемой величины, обладающую наименьшей дисперсией и, следовательно, наибольшей точностью по сравнению со всеми другими мыслимыми оценками. Поскольку эти оценки связаны с соответствующими случайными погрешностями , то можно записать равенство:
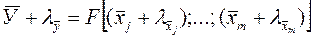, (2.20)
где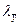 
- случайная погрешность оценки ;
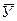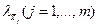- случайная погрешность оценки .
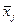Естественно предположить, что относительные случайные погрешности оценок малы по сравнению с единицей:
. (2.21)
Тогда уравнение (2.20) можно разложить в m-мерный ряд Тейлора по степеням случайных погрешностей. Ограничимся только первой степенью:
. (2.22)
Полученное таким образом равенство сводится к следующим двум: 
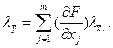(2.23)
Вычислим теперь дисперсию 
случайной погрешности 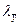оценки :
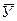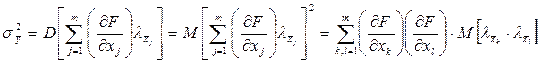(2.24)
Для математических ожиданий произведений 
случайных погрешностей имеем
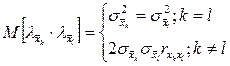(2.24)
Поэтому можно записать
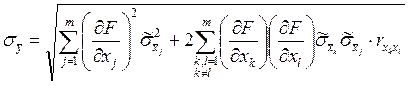(2.25)
Поскольку коэффициенты корреляции 
не зависят от значений оценок 
и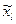 
, то из выражения (2.25) следует, что дисперсия оценки косвенно измеряемой величины достигает минимума в том случае, когда из возможных оценок исходных величин выбраны те, дисперсии которых минимальны. Такими оценками для измеряемых прямыми способами величин являются средние арифметические соответствующих рядов наблюдений.
Произведения частных производных уравнения косвенного измерения на с.к.о. результатов измерения соответствующих аргументов называются частными погрешностями косвенного измерения:
. (2.26)
Таким образом, в качестве наиболее достоверного значения 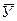косвенного измеряемой величины Y следует понимать значение, получаемое подстановкой в формулу (2.19) косвенного измерения средних арифметических 
рядов измерений искомых величин, т.е. путем применения формулы (18); с.к.о. этой оценки определяется из формулы:
, (2.27)
причем значения частных производных вычисляются при средних арифметических значениях аргументов .
Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений. В этих условиях для вычисления доверительного интервала случайной погрешности 
, рассчитываемого по формуле :
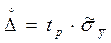, (2.28)
используется значение коэффициента tр , прямо выбираемое из таблицы при количестве измерений n > 30. Если же n ≤ 30, предварительно должно быть определено «эффективное» число степеней свободы, которое затем учитывает при определении tр из таблицы:
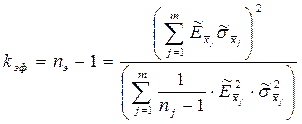, (2.29)
где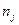 
- число прямых измерений величины 
.
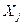Не все частные погрешности косвенного измерения оказывают одинаковое влияние на формирование итоговой погрешности результата косвенного измерения. Некоторые из них могут быть значительно меньше других, а поскольку значение погрешности все равно должно округляться до двух значащих цифр, они не будут оказывать заметного влияния на значение погрешности.
Если в равенстве
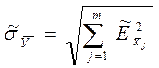
k-я частная погрешность такова, что
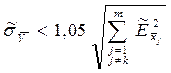, (2.30)
то этой погрешностью можно пренебречь, поскольку при округлении уже 1,0499… принимается за 1,0.
Возведя обе части неравенства (2.30) в квадрат и приняв во внимание, что
,
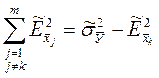получим
,
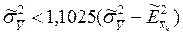откуда следует, что частными погрешностями, меньшими
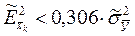
можно пренебречь. Округлив последнее неравенство, получим:
. (2.31)
Эта формула в метрологии называется критерием ничтожных погрешностей, а сами погрешности, отвечающие условию (2.31), называются ничтожными или ничтожно малыми.
Формула (2.31) легко распространяется на случай нескольких погрешностей и приводит к следующему критерию ничтожности суммы квадратов частных погрешностей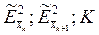 
:
.
Использование критерия ничтожных погрешностей позволяет найти те величины , повышение точности , измерение которых позволяет уменьшить суммарную погрешность результата. Очевидно, не имеет смысла повышать точность измерения тех величин, частные погрешности которых и без того ничтожно малы.
Алгоритм обработки результатов косвенных измерений приведен на рисунке 2.4