Последовательное соединение резистивного, индуктивного и емкостного элементов
Рассмотрим схему, состоящую из резистора, индуктивности и емкости (рис. 5.10)
 |
Подадим на вход этой схемы синусоидальное напряжение
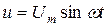 .
. Для упрощения расчетов будем полагать, что начальная фаза напряжения равна нулю.
По второму закону Кирхгофа напряжение на входе цепи равно сумме падений напряжения на элементах:
 .
.
Поскольку через все элементы цепи протекает один и тот же ток, выразим все напряжения через ток
 .
.
С учетом этого второй закон Кирхгофа запишется
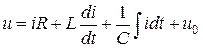 .
.
В это выражение ток входит в алгебраической, дифференциальной и интегральной формах, что усложняет решение уравнения. Свести уравнение к алгебраической форме позволяет символический метод. Запишем это уравнение в комплексной форме
 .
.
Разделив напряжение на ток, получим полное сопротивление цепи
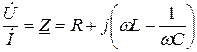 .
.
Но 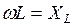 – это индуктивное сопротивление цепи,
– это индуктивное сопротивление цепи, 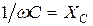 – это емкостное сопротивление. Следовательно, полное комплексное сопротивление цепи можно записать
– это емкостное сопротивление. Следовательно, полное комплексное сопротивление цепи можно записать
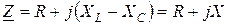 ,
,
где 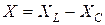 – общее реактивное сопротивление цепи.
– общее реактивное сопротивление цепи.
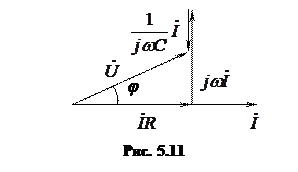 |
Построим векторную диаграмму этой цепи (рис. 5.11).
Так как по всем элементам цепи протекает один и тот же ток, построение диаграммы начинаем с вектора тока  , направив его вдоль действительной оси.
, направив его вдоль действительной оси.
Строим диаграмму напряжений в соответствии с уравнением по второму закону Кирхгофа, последовательно суммируя напряжения. Учитываем, что напряжение на резисторе совпадает по фазе с током, откладываем вектор этого напряжения вдоль вектора тока. Напряжение на индуктивности опережает ток на угол 90о, напряжение на емкости отстает от тока на 90о. Результирующий вектор  представляет собой напряжение на входе цепи.
представляет собой напряжение на входе цепи.
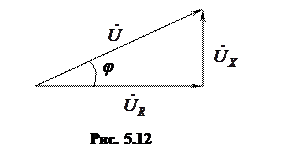 В результате того, что цепь содержит и резистивный, и реактивные элементы, сдвиг фаз между током и напряжением будет отличен как от нуля, так и от 90о.
В результате того, что цепь содержит и резистивный, и реактивные элементы, сдвиг фаз между током и напряжением будет отличен как от нуля, так и от 90о.
Из векторной диаграммы выделяют треугольник напряжений (рис. 5.12). Этот треугольник – векторный. Катетами треугольника являются активное и реактивное напряжения, гипотенузой – напряжение на входе цепи. Под реактивным напряжением понимают векторную сумму индуктивного и емкостного напряжений 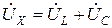 . Модуль этой величины равен разности модулей
. Модуль этой величины равен разности модулей
 .
.
Из треугольника напряжений следует, что модуль полного напряжения равен
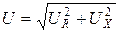 .
.
Сдвиг фаз между током и напряжением в цепи можно определить по формуле
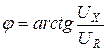 .
.
Если известны входное напряжение и угол φ, то можно определить активную и реактивную составляющие напряжения:
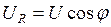 ;
; 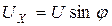 .
.
 Если поделим все стороны треугольника напряжений на одну и ту же величину тока, то получим подобный ему треугольник сопротивлений (рис. 5.13), сторонами которого являются:
Если поделим все стороны треугольника напряжений на одну и ту же величину тока, то получим подобный ему треугольник сопротивлений (рис. 5.13), сторонами которого являются:
z – модуль полного сопротивления цепи;
R – активное сопротивление всей цепи;
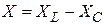 – модуль реактивного сопротивления цепи.
– модуль реактивного сопротивления цепи.
Из треугольника сопротивлений можно определить:
модуль полного сопротивления цепи 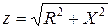 ;
;
разность фаз напряжения и тока  ;
;
активное сопротивление цепи 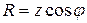 ;
;
реактивное сопротивление цепи  .
.
