D.3. Системы эконометрических уравнений
Пример решения типовой задачи смотри в разделе 3.
Варианты индивидуальных заданий
Даны системы эконометрических уравнений.
Требуется
1.Применив необходимое и достаточное условие идентификации, определите, идентифицируемо ли каждое из уравнений модели.
2.Определите метод оценки параметров модели.
3.Запишите в общем виде приведенную форму модели.
Вариант 1
Модель протекционизма Сальватора (упрощенная версия):

где  – доля импорта в ВВП;
– доля импорта в ВВП; 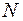 – общее число прошений об освобождении от таможенных пошлин;
– общее число прошений об освобождении от таможенных пошлин; 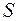 – число удовлетворенных прошений об освобождении от таможенных пошлин;
– число удовлетворенных прошений об освобождении от таможенных пошлин; 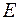 – фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет;
– фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет;  – реальный ВВП;
– реальный ВВП;  – реальный объем чистого экспорта;
– реальный объем чистого экспорта;  – текущий период;
– текущий период; 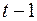 – предыдущий период.
– предыдущий период.
Вариант 2
Макроэкономическая модель (упрощенная версия модели Клейна):
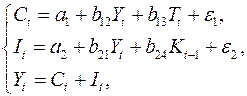
где 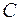 – потребление;
– потребление; 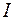 – инвестиции;
– инвестиции;  – доход;
– доход; 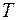 – налоги;
– налоги; 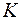 – запас капитала;
– запас капитала;  – текущий период;
– текущий период; 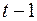 – предыдущий период.
– предыдущий период.
Вариант 3
Макроэкономическая модель экономики США (одна из версий):
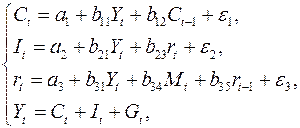
где 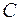 – потребление;
– потребление;  – ВВП;
– ВВП; 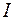 – инвестиции;
– инвестиции;  – процентная ставка;
– процентная ставка;  – денежная масса;
– денежная масса; 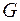 – государственные расходы;
– государственные расходы;  – текущий период;
– текущий период; 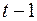 – предыдущий период.
– предыдущий период.
Вариант 4
Модель Кейнса (одна из версий):

где 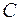 – потребление;
– потребление;  – ВВП;
– ВВП; 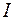 – валовые инвестиции;
– валовые инвестиции; 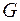 – государственные расходы;
– государственные расходы;  – текущий период;
– текущий период; 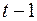 – предыдущий период.
– предыдущий период.
Вариант 5
Модель денежного и товарного рынков:
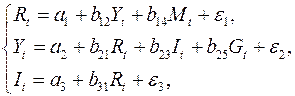
где 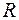 – процентные ставки;
– процентные ставки;  – реальный ВВП;
– реальный ВВП;  – денежная масса;
– денежная масса; 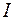 – внутренние инвестиции;
– внутренние инвестиции; 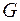 – реальные государственные расходы.
– реальные государственные расходы.
Вариант 6
Модифицированная модель Кейнса:

где 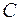 – потребление;
– потребление;  – доход;
– доход; 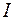 – инвестиции;
– инвестиции; 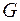 – государственные расходы;
– государственные расходы;  – текущий период;
– текущий период; 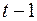 – предыдущий период.
– предыдущий период.
Вариант 7
Макроэкономическая модель:
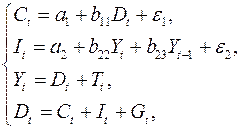
где 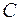 – расходы на потребление;
– расходы на потребление;  – чистый национальный продукт;
– чистый национальный продукт;  – чистый национальный доход;
– чистый национальный доход; 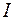 – инвестиции;
– инвестиции; 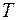 – косвенные налоги;
– косвенные налоги; 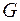 – государственные расходы;
– государственные расходы;  – текущий период;
– текущий период; 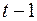 – предыдущий период.
– предыдущий период.
Вариант 8
Гипотетическая модель экономики:

где 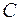 – совокупное потребление в период
– совокупное потребление в период  ;
;  – совокупный доход в период
– совокупный доход в период  ;
; 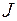 – инвестиции в период
– инвестиции в период  ;
; 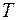 – налоги в период
– налоги в период  ;
; 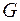 – государственные доходы в период
– государственные доходы в период  .
.
Вариант 9
Модель денежного рынка:

где 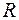 – процентные ставки;
– процентные ставки;  – ВВП;
– ВВП;  – денежная масса;
– денежная масса; 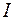 – внутренние инвестиции.
– внутренние инвестиции.
Вариант 10
Конъюнктурная модель имеет вид:
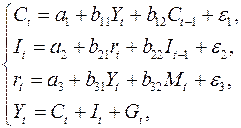
где 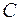 – расходы на потребление;
– расходы на потребление;  – ВВП;
– ВВП; 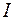 – инвестиции;
– инвестиции;  – процентная ставка;
– процентная ставка;  – денежная масса;
– денежная масса; 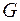 – государственные расходы;
– государственные расходы;  – текущий период;
– текущий период; 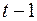 – предыдущий период.
– предыдущий период.
D.4. Временные ряды
Пример решения типовой задачи смотри в разделе 4.
Варианты индивидуальных заданий
Имеются условные данные об объемах потребления электроэнергии (  ) жителями региона за 16 кварталов.
) жителями региона за 16 кварталов.
Требуется:
1.Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2.Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов).
3.Сделать прогноз на 2 квартала вперед.
Варианты 1, 2
 |  |  |  |
| 5,8 | 7,9 | ||
| 4,5 | 5,5 | ||
| 5,1 | 6,3 | ||
| 9,1 | 10,8 | ||
| 7,0 | 9,0 | ||
| 5,0 | 6,5 | ||
| 6,0 | 7,0 | ||
| 10,1 | 11,1 |
Варианты 3, 4
 |  |  |  |
| 5,5 | 8,0 | ||
| 4,6 | 5,6 | ||
| 5,0 | 6,4 | ||
| 9,2 | 10,9 | ||
| 7,1 | 9,1 | ||
| 5,1 | 6,4 | ||
| 5,9 | 7,2 | ||
| 10,0 | 11,0 |
Варианты 5, 6
 |  |  |  |
| 5,3 | 8,2 | ||
| 4,7 | 5,5 | ||
| 5,2 | 6,5 | ||
| 9,1 | 11,0 | ||
| 7,0 | 8,9 | ||
| 5,0 | 6,5 | ||
| 6,0 | 7,3 | ||
| 10,1 | 11,2 |
Варианты 7, 8
 |  |  |  |
| 5,5 | 8,3 | ||
| 4,8 | 5,4 | ||
| 5,1 | 6,4 | ||
| 9,0 | 10,9 | ||
| 7,1 | 9,0 | ||
| 4,9 | 6,6 | ||
| 6,1 | 7,5 | ||
| 10,0 | 11,2 |
Варианты 9, 10
 |  |  |  |
| 5,6 | 8,2 | ||
| 4,7 | 5,6 | ||
| 5,2 | 6,4 | ||
| 9,1 | 10,8 | ||
| 7,0 | 9,1 | ||
| 5,1 | 6,7 | ||
| 6,0 | 7,5 | ||
| 10,2 | 11,3 |
Приложение Е
