Частные производные

Тема 2.4 Функции нескольких переменных.

Основные понятия.

При рассмотрении многих вопросов из различных областей знания приходится изучать такие зависимости между переменными величинами, когда числовые значения одной из них полностью определяются значениями нескольких других.

Например, изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами: x, y, z. Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных: x, y, z. Если физическое состояние тела к тому же еще и меняется с течением времени t, то та же плотность будет зависеть уже от значений четырех переменных: x, y, z, t.

Другой пример: изучаются издержки производства на изготовление единицы некоторого вида продукции. Пусть:

x - затраты по материалам,

y - расходы на выплату заработной платы работникам,

z - амортизационные отчисления.

Очевидно, что издержки производства зависят от значений названных параметров x, y, z.

Определение.Если каждой совокупности значений n переменных 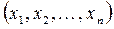из некоторого множества D этих совокупностей соответствует своё единственное значение переменной z, то говорят, что на множестве D задана функция n переменных.

Множество D называется областью определения или областью существования этой функции.

Если рассматривается функция двух переменных, то совокупности чисел

обозначаются, как правило, (x, y) и интерпретируются как точки координатной плоскости Oxy, а область определения функции z = f ( x, y ) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy.

Так, например, областью определения функции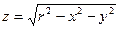

является множество точек плоскости Oxy, координаты которых удовлетворяют соотношению

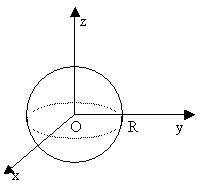
т. е. представляет собой круг радиуса r с центром в начале координат.

Для функции

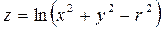областью определения служат точки, которые удовлетворяют условию т. е. внешние точки по отношению к заданному кругу.

Часто функции двух переменных задаются в неявном виде, т. е. как уравнение

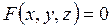,связывающее три переменные величины. В этом случае каждую из величин x, y, z можно рассматривать как неявную функцию двух остальных.

Геометрическим изображением (графиком) функции двух переменных z = f ( x, y ) является множество точек P ( x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z = f ( x, y ) (плоскости, цилиндры, шары, параболоиды и т.д.).

Графиком функции непрерывных аргументов, как правило, является некоторая поверхность в пространстве Oxyz, которая проектируется на координатную плоскость Oxy в область определения функции z= f ( x, y ).

Так, например, графиком функции является верхняя половина сферы, а графиком функции 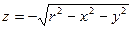- нижняя половина сферы:

Графиком линейной функции z = ax + by + с является плоскость в пространстве Oxyz, а графиком функции z = сonst служит плоскость, параллельная координатной плоскости Oxyz.

Заметим, что функцию трех и большего числа переменных изобразить наглядно в виде графика в трехмерном пространстве невозможно.

Частные производные.

Определение. Частной производной от функции по независимой переменной 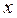называется производная

, вычисленная при постоянном .

То есть когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом).

Частной производной от функции 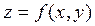по независимой переменной называется производная

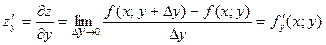, вычисленная при постоянном .

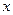То есть когда мы находим частную производную по «игрек», то переменная 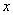считается константой (постоянным числом).

Для частных производных справедливы обычные правила и формулы дифференцирования.

Следующий пример демонстрирует применение частных производных на практике:

Количественная величина потока П пассажиров железных дорог может быть выражена функцией

где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстоянии между пунктами.

Частная производная функции П по R, равная

показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.

Частная производная П по N, равная

показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населённых пунктов при одном и том же расстоянии между пунктами.

Примеры.

а) Найти частные производные функции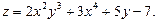

Решение.

1.Считаем переменную y константой и применяем правила дифференцирования:

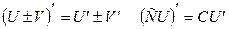
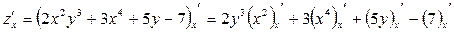
2. Используем табличные производные:

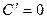
3. Теперь считаем переменную х константой и применяем те же правила дифференцирования и табличные производные:

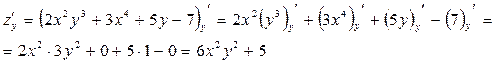
б) Найти частные производные функции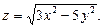

Решение.

1. Считаем переменную y константой, применяем правило дифференцирования сложной функции, правило дифференцирования суммы, правило вынесение постоянного множителя за знак производной и табличную производную:

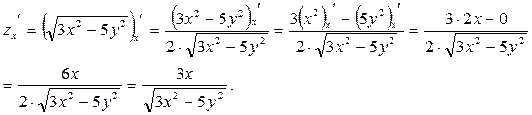
2. Теперь считаем переменную х константой и применяем те же правила дифференцирования и табличные производные: