В прямокутній трапеції основи дорівнюють 25 см і 37 см, а менша діагональ є бісектрисою тупого кута. Знайдіть площу трапеції. Варіант 11
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть площу прямокутної трапеції, основи якої 4 см та 6 см, а менша бічна сторона дорівнює 3 см.
А) 72 см2; Б) 18 см2;
В) 15 см2; Г) 12 см2.
2. Знайдіть кути трикутника АВС, якщо 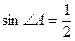 ,
, 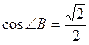 .
.
А)  А=60°,
А=60°,  В=30°,
В=30°,  C=90°; Б)
C=90°; Б)  А=30°,
А=30°,  В=45°,
В=45°,  C=105°;
C=105°;
В)  А=90°,
А=90°,  В=45°,
В=45°,  C=45°; Г)
C=45°; Г)  А=60°,
А=60°,  В=60°,
В=60°,  C=60°.
C=60°.
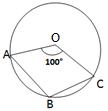 3. О – центр кола. Знайдіть кут АВС.
3. О – центр кола. Знайдіть кут АВС.
А) 150°; Б) 200°;
В) 130°; Г) 260°.
4. Менша основа трапеції дорівнює 5 см, а середня лінія — 8 см. Знайдіть більшу основу трапеції.
А) 22 см; Б) 11 см;
В) 27 см; Г) 16 см.
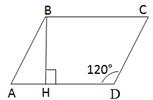 5. АВСD – паралелограм, СD = 3 см. Знайдіть ВН.
5. АВСD – паралелограм, СD = 3 см. Знайдіть ВН.
А) 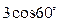 ; Б)
; Б) 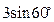 ;
;
В) 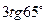 ; Г)
; Г) 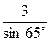 .
.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. У паралелограмі бісектриса кута ділить протилежну сторону на відрізки, які дорівнюють 3,7 дм і 5,9 дм. Обчисліть периметр паралелограма.
7. Сторони трикутника відносяться як 2 : 4 : 5. Знайдіть сторони подібного йому трикутника, якщо різниця найбільшої та найменшої сторін другого трикутника дорівнює 12 см.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. Медіана, проведена до гіпотенузи прямокутного трикутника, ділить прямий кут у відношенні 1 : 2 та дорівнює 16 см. Знайдіть площу трикутника.
Варіант 12
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть висоту трапеції, площа якої дорівнює 90 см2, а сума основ 30 см.
А) 12 см; Б) 6 см;
В) 3 см; Г) 18 см.
2. Знайдіть кути трикутника АВС, якщо 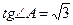 ,
, 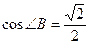 .
.
А)  А=60°,
А=60°,  В=45°,
В=45°,  C=75°; Б)
C=75°; Б)  А=45°,
А=45°,  В=45°,
В=45°,  C=90°;
C=90°;
В)  А=30°,
А=30°,  В=45°,
В=45°,  C=105°; Г)
C=105°; Г)  А=60°,
А=60°,  В=60°,
В=60°,  C=60°.
C=60°.
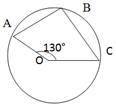 3. О – центр кола. Знайдіть
3. О – центр кола. Знайдіть  АВС.
АВС.
А) 115°; Б) 75°;
В) 250°; Г) 230°.
4. Більша основа трапеції дорівнює 11 см, а середня лінія — 8 см. Знайдіть меншу основу трапеції.
А) 21 см; Б) 10 см;
В) 5 см; Г) 8 см.
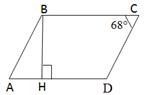 5. АВСD – паралелограм, АВ = 4 см. Знайдіть АН.
5. АВСD – паралелограм, АВ = 4 см. Знайдіть АН.
А) 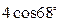 ; Б)
; Б) 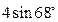 ;
;
В) 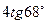 ; Г)
; Г) 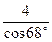 .
.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. У паралелограмі бісектриса кута ділить протилежну сторону на відрізки, які дорівнюють 4,5 дм і 7,3 дм. Обчисліть периметр паралелограма.
7. Сторони трикутника відносяться як 3 : 5 : 6. Знайдіть сторони подібного йому трикутника, якщо сума найбільшої та найменшої сторін другого трикутника дорівнює 27 см.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. Медіана, проведена до гіпотенузи прямокутного трикутника, ділить прямий кут на два кути, різниця яких дорівнює 30°. Радіус описаного кола дорівнює 18 см. Знайдіть площу трикутника.
Варіант 13
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть усі кути паралелограма, якщо різниця двох із них дорівнює 60°.
А) 130°, 70°, 130°, 70°; Б) 110°, 50°, 110°, 50°;
В) 125°, 65°, 125°, 65°; Г) 120°, 60°, 120°, 60°.
2. Одна з основ трапеції дорівнює 9 см. Знайдіть її другу основу, якщо середня лінія трапеції дорівнює 5 см.
А) 4 см; Б) 1 см;
В) 28 см; Г) 13 см.
3. Точка знаходиться від прямої на відстані 5 см. З неї до прямої проведено похилу, яка утворює з прямою кут 45°. Знайдіть проекцію похилої на цю пряму.
А) 10 см; Б) 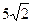 см;
см;
 В) 5 см; Г) 2,5 см.
В) 5 см; Г) 2,5 см.
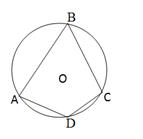
4. О – центр кола.  АВС = х,
АВС = х,  АDС = 3х. Знайдіть
АDС = 3х. Знайдіть  D.
D.
А) 130°; Б) 120°;
В) 135°; Г) не можна визначити.
5. В прямокутному трикутнику MNK, PK = 5 см, MP = 20 см. Знайдіть NP.
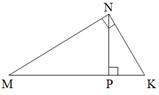 А) 8 см; Б) 10 см ;
А) 8 см; Б) 10 см ;
В) 18 см; Г) 14 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. З точки поза прямою проведено дві похилі до цієї прямої. Перша з них дорівнює 13 см, її проекція – 12 см. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 30°.
7. Дві сторони трикутника дорівнюють 18 см та 24 см, а висота, яка проведена до меншої з них, дорівнює 22 см. Знайдіть висоту, яку проведено до більшої з них.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. З точки кола, довжина якого дорівнює 52π см, проведено перпендикуляр на його діаметр. Обчисліть довжини відрізків, на які він ділить діаметр, якщо довжина перпендикуляра дорівнює 24 см.
Варіант 14
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Знайдіть усі кути паралелограма, якщо сума двох із них дорівнює 100°.
А) 50°, 120°, 50°, 120°; Б) 130°, 50°, 130°, 50°;
В) 70°, 60°, 70°, 60°; Г) 50°, 80°, 50°, 80°.
2. Знайдіть середню лінію трапеції, якщо її основи дорівнюють 106дм та 326дм.
А) 216 дм; Б) 432 дм;
В) 220 дм; Г) 110 дм.
3. Точка знаходиться на відстані 7 см від прямої. З цієї точки до прямої проведено похилу, яка утворює з прямою кут 30°. Знайдіть довжину похилої.
А) 3.5 см; Б) 14 см;
В) 7 см; Г) 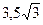 см.
см.
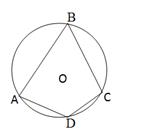 4. О – центр кола.
4. О – центр кола. 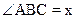 ,
, 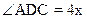 . Знайдіть
. Знайдіть 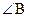 .
.
А) 36°; Б) 60°;
В) 20°; Г) не можна визначити.
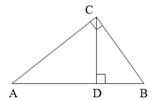 5. В прямокутному трикутнику АСВ, АС = 16 см, АD = 8 см. Знайдіть АВ.
5. В прямокутному трикутнику АСВ, АС = 16 см, АD = 8 см. Знайдіть АВ.
А) 2 4см; Б) 28 см;
В) 20 см; Г) 32 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. З точки поза прямою проведені до прямої дві похилі. Перша з них дорівнює 15 см, її проекція – 12 см. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 45°.
7. Дві сторони трикутника дорівнюють 20 см та 22 см, а висота, яку проведено до більшої з них, дорівнює 15 см. Знайдіть висоту, яку проведено до меншої з них.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
З точки кола до діаметра проведено перпендикуляр, який ділить діаметр на відрізки у відношенні 4 : 9. Обчисліть довжину цього перпендикуляра, якщо довжина кола 52π см. Варіант 15
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Точка перетину діагоналей квадрата віддалена від його сторін на 5 см. Знайдіть периметр квадрата.
А) 80 см; Б) 20 см;
В) 40 см; Г) 30 см.
2. АВСD – прямокутник,  АВD більший за
АВD більший за  СВD на 20°. Знайдіть кути
СВD на 20°. Знайдіть кути 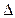 АОВ, якщо О – точка перетину діагоналей.
АОВ, якщо О – точка перетину діагоналей.
А) 20°, 20°, 140°; Б) 70°, 70°, 40°;
В) 35°, 35°, 110°; Г) 70°, 55°, 55°.
3. Кола, радіуси яких дорівнюють 30 см та 40 см, мають зовнішній дотик. Знайдіть відстань між їх центрами.
А) 50 см; Б) 10 см;
В) 70 см; Г) 60 см.
4. Сторона правильного трикутника дорівнює 6 см. Знайдіть його площу.
А) 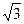 см2 ; Б)
см2 ; Б) 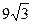 см2;
см2;
В) 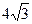 см2; Г)
см2; Г) 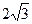 см2.
см2.
5. Основа рівнобедреного трикутника дорівнює16 см, а висота, яку проведено до основи, - 6 см. Знайдіть бічну сторону трикутника.
А) 11 см; Б) 10 см;
В) 22 см; Г) 14 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. У рівнобічній трапеції АВСD висота, проведена з вершини С, ділить більшу основу на відрізки, що відносяться, як 10 : 4. Середня лінія трапеції 40 см. Знайдіть меншу основу трапеції.
7. Різниця градусних мір центрального і вписаного кутів, що спираються на одну й ту саму дугу, дорівнює 64°. Знайдіть градусні міри обох кутів.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. У рівнобічній трапеції більша основа дорівнює 2,7 м, бічна сторона 1 м, а кут між ними 60°. Знайдіть меншу основу трапеції.
Варіант 16
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Точка перетину діагоналей квадрата віддалена від його сторін на 8 см. Знайдіть периметр квадрата.
А) 64 см; Б) 32 см;
В) 48 см; Г) 96 см.
2. АВСD – прямокутник, 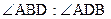 = 4 : 5. Знайдіть кути
= 4 : 5. Знайдіть кути 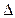 АОВ, якщо О – точка перетину діагоналей.
АОВ, якщо О – точка перетину діагоналей.
А) 50°, 50°, 80°; Б) 50°, 90°, 40°;
В) 40°, 40°, 100°; Г) 70°, 70°, 40°.
3. Кола, радіуси яких дорівнюють 3 см та 2 см, мають внутрішній дотик. Знайдіть відстань між їх центрами.
А) 10 см; Б) 8 см;
В) 5 см; Г) 1 см.
4. Сторона правильного трикутника дорівнює 4 см. Знайдіть його площу.
А) 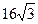 см2 ; Б)
см2 ; Б) 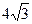 см2;
см2;
В) 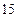 см2; Г)8 см2.
см2; Г)8 см2.
5. Бічна сторона рівнобедреного трикутника дорівнює 5 см, а його основа - 8 см. Знайдіть висоту цього трикутника, проведену до основи.
А) 9 см; Б) 4 см;
В) 3 см; Г) 14 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. У рівнобічній трапеції АВСD висота, проведена з вершини В , ділить більшу основу на відрізки, різниця яких дорівнює 4 см. Середня лінія трапеції 22 см. Знайдіть більшу основу трапеції.
7. Сума градусних мір центрального і вписаного кутів, що спираються на одну й ту саму дугу, дорівнює 120°. Знайдіть градусні міри обох кутів.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
8. Знайдіть периметр рівнобічної трапеції, якщо більша основа дорівнює 5,4 см, бічна сторона 2 см, а кут між ними 60°.
Варіант 17
I частина (5 балів)
Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.
1. Сума двох кутів ромба дорівнює 108°. Знайдіть кути одного з трикутників, на які ромб ділиться його діагоналями.
А) 90°, 63°, 27°; Б) 90°, 54°, 36°;
В) 90°, 45°, 45°; Г) 90°, 37°, 53°.
2. В рівнобічній трапеції АВСD проведені висоти ВК і СМ. Менша основа дорівнює 6 см. АК = МD = 4 см. Знайдіть більшу основу.
А) 24 см; Б) 20 см;
В) 14 см; Г) 10 см.
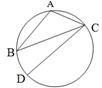 3. Дано:
3. Дано:  ВСD=21°.
ВСD=21°.  АСВ=49°, DС – діаметр кола. Знайти
АСВ=49°, DС – діаметр кола. Знайти  АВС.
АВС.
А) 20°; Б) 25°;
В) 18°; Г) 28°.
4. В прямокутному трикутнику АВС кут В – прямий. Знайдіть косинус кута А.
 А)
А) 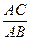 ; Б)
; Б) 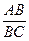 ;
;
В) 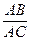 ; Г)
; Г) 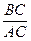 .
.
5. Обчисліть радіус кола, описаного навколо прямокутного трикутника, якщо його катети дорівнюють 40 см та 30 см.
А) 12,5 см; Б) 50 см;
В) 25 см; Г) 70 см.
ІІ частина (4 бали)
Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.
6. З точки В до прямої a проведено дві похилі: ВА = 20 см і ВС = 13 см. Проекція похилої ВА більша за проекцію похилої ВС на 11 см. Знайдіть проекції цих похилих.
7. Сторони паралелограма дорівнюють 15 см і 20 см, а відстань між меншими сторонами дорівнює 4 см. Знайдіть відстань між більшими сторонами паралелограма.
ІІІ частина (3 бали)
Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.
