Задания для самопроверки №3

1. Постройте на бумаге в клетку систему координат, где единичный отрезок - 1см. Найдите приближенные значения следующих интервалов с помощью графиков подынтегральных функций:

a) ;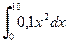

b) ;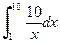

c) .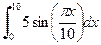

2. Пусть имеется кардиоида 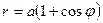(рис. см. приложение №1). Найти:

a) площадь фигуры ограниченной кардиоидой ; Ответ: .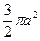

b) длину дуги кардиоиды; Ответ: 8а.

3.Пусть имеется одна арка циклоиды 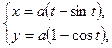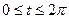, ограниченная осью Ох (рис. см. приложение №1). Найти:

a) площадь циклоиды Ответ: .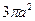

b) длину дуги циклоиды; Ответ: 8а.

c) вычислить объём тела, образованного вращением вокруг оси Ох одной арки циклоиды. Ответ: 5π²а³.

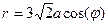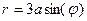4. Вычислить площадь фигуры, ограниченной окружностями и . Ответ: .

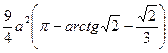5. Определить площадь части круга 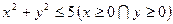, ограниченной кривыми 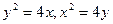. Ответ: .

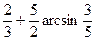6.Найти силу давления бензина, находящегося в цилиндрическом баке высокой h = 3,5 м и радиусом основания r = 1,5 м, на его стенки, если 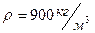. Ответ: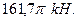

7.Найти работу, совершенную при выкачивании воды из емкости, имеющую форму полуцилиндра, длина которого a, радиус r.

Ответ: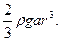

8. Вычислить силу давления воды на пластину, имеющую форму параллелограмма с основанием а = 2 м и высота Н = 3 м, опущенную вертикально вниз на глубину 4 м, если основание параллельно поверхности воды. Плотность воды 1 т/м³.

Ответ: 156,8 кН.

9. Найти координаты центра масс однородной дуги окружности радиусом R с центром в начале координат, расположенной в первом квадранте.

Ответ: ( ; ).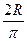

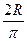10. Найти координаты центра масс однородной фигуры, ограниченной линиями .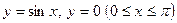

Ответ: ( ; ).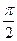

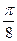11. Вычислить работу, необходимую для того, чтобы выкачать воду из полусферического сосуда, диаметр которого 20 м, если плотность воды 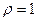т/м³.

Ответ: 76969 кДж.

12. Найти координаты центра масс однородной плоской фигуры, ограниченной линиями .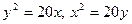

Ответ: (9;9).

13. Производительность труда рабочего в течение дня задается функцией 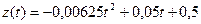(ден.ед./ч.), где t – время в часах от начала работы, 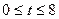. Найти функцию u=u(t), выражающую объем продукции (в стоимостном выражении) и его величину за рабочий день.

Ответ: 4,53 ден. ед.

14. Стоимость перевозки одной тонны груза на один километр (тариф перевозки) задается функцией 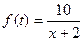(ден.ед./км.). Определите затраты на перевозку одной тонны груза на расстояние 20 км.

Ответ: 23,98 ден. ед.

15. Вычислить среднюю теплоемкость аммиака 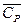в интервале температур от 298 до 1000 К.

Ответ: 45,79 Дж/(моль К).

Вопросы и предложения для самопроверки

Неопределенный интеграл

1. Что называется неопределенным интегралом от данной функции?

2. Что называется первообразной от данной функции?

3. Сформулируйте теорему о существовании неопределенного интеграла.

4. Сформулируйте свойства неопределенного интеграла.

5. В чем состоит метод интегрирования по частям в неопределенном интеграле?

6. Какая рациональная дробь называется правильной?

7. Как производится разложение правильной рациональной дроби на простейшие?

8. В чем состоит метод интегрирования рациональной функции?

9. Приведите примеры интегрирования простейших иррациональных функций.

Определенный интеграл

10. Что называется определенным интегралом от данной функции в данном интервале?

11. В чем состоит теорема существования определенного интеграла?

12. Сформулируйте свойства определенного интеграла.

13. Каков геометрический смысл определенного интеграла от данной функции 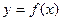в данном интервале 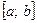в системе декартовых координат?

14. Разъясните понятие интеграла как функции своего верхнего предела.

15. Сформулируйте теорему о связи между неопределённым интегралом и определённым интегралами.

16. В чем состоит метод замены переменной в определенном интеграле?

17. В чем особенность вычисления определенного интеграла, взятого по симметричному интервалу ?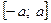

18. Что называется несобственным интегралом от данной функции по бесконечному интервалу?

19. Что называется несобственным интегралом от данной функции по данному конечному интервалу?