Дисперсия. Среднее квадратическое отклонение

Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. В зависимости от исходных данных дисперсия может быть невзвешенной (простой) или взвешенной.

Дисперсия рассчитывается по следующим формулам:

· для несгруппированных данных

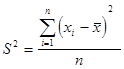
· для сгруппированных данных

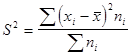
Порядок расчета дисперсии взвешенную:

1. определяют среднюю арифметическую взвешенную

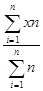
2. определяются отклонения вариант от средней

3. возводят в квадрат отклонение каждой варианты от средней

4. умножают квадраты отклонений на веса (частоты)

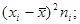
5. суммируют полученные произведения

6. полученную сумму делят на сумму весов

Формула для определения дисперсии может быть преобразована в следующую формулу:

- простая

Порядок расчета дисперсии простой:

1. определяют среднюю арифметическую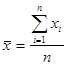

2. возводят в квадрат среднюю арифметическую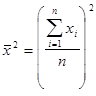

3. возводят в квадрат каждую варианту ряда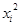

4. находим сумму квадратов вариант

5. делят сумму квадратов вариант на их число, т.е. определяют средний квадрат

=

6. определяют разность между средним квадратом признака и квадратом средней

Также формула для определения дисперсии взвешенной может быть преобразована в следующую формулу:

т.е. дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической. При пользовании преобразованной формулой исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от х и исключается ошибка в расчете, связанная с округлением отклонений

Дисперсия обладает рядом свойств, некоторые из них позволяют упростить ее вычисления:

1) дисперсия постоянной величины равна нулю;

2) если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится;

3) если все варианты значений признака уменьшить в одно и то же число раз ( 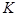раз), то дисперсия уменьшится в раз

Среднее квадратичное отклонение S - представляет собой корень квадратный из дисперсии:

· для несгруппированных данных:

;

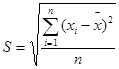· для вариационного ряда:

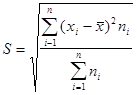
Размах вариации, среднее линейное и среднее квадратичное отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.

Дисперсия и среднее квадратическое отклонение наиболее широко применяемые показатели вариации. Объясняется это тем, что они входят в большинство теорем теории вероятности, служащей фундаментом математической статистики. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.

Расчет показателей вариации для банков, сгруппированных по размеру прибыли, показан в таблице.

Размер прибыли, млн. руб.	Число банков	расчетные показатели
3,7 - 4,6 (-)		4,15	8,30	-1,935	3,870	7,489
4,6 - 5,5		5,05	20,20	- 1,035	4,140	4,285
5,5 - 6,4		5,95	35,70	- 0,135	0,810	0,109
6,4 - 7,3		6,85	34,25	+0,765	3,825	2,926
7,3 - 8,2		7,75	23,25	+1,665	4,995	8,317
Итого:			121,70		17,640	23,126

Среднее линейное и среднее квадратичное отклонение показывают на сколько в среднем колеблется величина признака у единиц и исследуемой совокупности. Так, в данном случае средняя величина колеблености размера прибыли составляет: по среднему линейному отклонению 0,882 млн. руб.; по среднему квадратическому отклонению - 1,075 млн. руб. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Если распределение признака, близко к нормальному, то между S и d существует взаимосвязь: S=1,25d, или d=0,8S. Среднее квадратическое отклонение показывает как расположена основная масса единиц совокупности относительно средней арифметической. Независимо от формы распределения 75 значений признака попадают в интервал х 2S, а по крайне мере 89 всех значений попадают интервал х 3S (теорема П.Л.Чебышева).