Сокращение дробей
2.1. Анализ преобразования
Переход от уравнения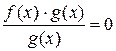 
к уравнению 
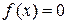в результате сокращения дроби расширяет область определения данного уравнения, следовательно, возможно появление посторонних корней. Иными словами, сокращение дроби может привести к уравнению – следствию, то есть к уравнению, не равносильному данному. Уравнение вида 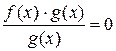равносильно системе 
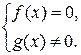Рассмотрим ряд примеров.
Пример 1. Решить уравнение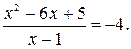 
Данное уравнение в области его определения равносильно уравнению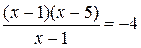 
. Ясно, что сократив дробь, мы расширим область определения уравнения. Однако переход к системе 
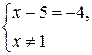сохранит равносильность. Полученная система решений не имеет.
Ответ: решений нет.
Пример 2. Решить уравнение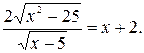 
Выполним преобразования дроби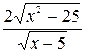 
:
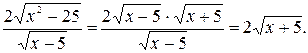Очевидно, что первое преобразование сохранило область определения дроби 
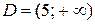, а второе (сокращение) расширило её до промежутка 
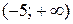. Следовательно, данное уравнение равносильно системе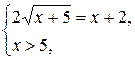 
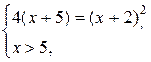
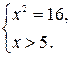
Система решений не имеет.
Ответ: решений нет.
Пример 3. Решить уравнение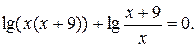 
Область определения данного уравнения D задаётся неравенством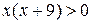 
, решая которое получим, 
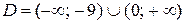. Используя свойство логарифмов и сокращая дробь, придём к уравнению 
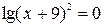с расширенной областью определения. Следовательно, данное уравнение равносильно системе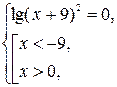 
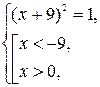
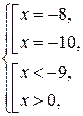
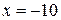- решение системы.
Ответ: -10.
Пример 4. Решить уравнение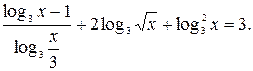 
Выполним тождественные преобразования левой части данного уравнения, не меняющие его область определения. Получим равносильное уравнение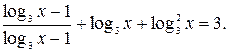 
Сокращение дроби 
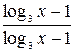расширит область определения данного уравнения, поэтому исходное уравнение равносильно системе
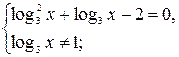
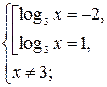
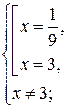
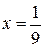- решение системы. Ответ: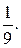 
Пример 5.Решить уравнение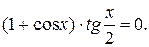 
Данное уравнение равносильно уравнению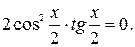 
Дальнейшее
сокращение дроби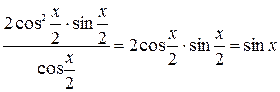 
расширит его область определения, что может привести к появлению посторонних решений. Таким образом, данное уравнение равносильно системе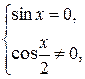 
, 
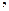
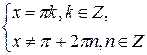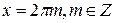- решения системы и данного уравнения. Ответ: 
.
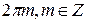Пример 6. Решить уравнение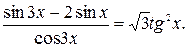 
Запишем цепочку уравнений, равносильных данному в области его определения:
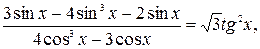
Последнее уравнение, полученное в результате сокращения дроби, равносильно системе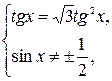 
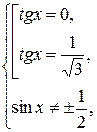
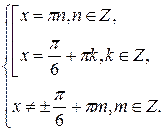
Для решение системы используем окружность.
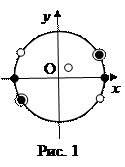
Ответ: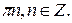 
2.2. Комплекс заданий.
Решить уравнение Ответ.
№ 1.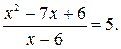 
Решений нет.
№ 2.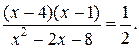 
Решений нет.
№ 3.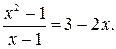 
.
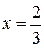№ 4.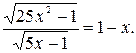 
Решений нет.
№ 5.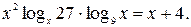 
2.
№ 6. 
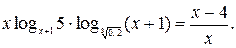1.
№ 7.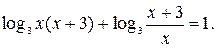 
.
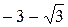№ 8. .
№ 9. .
№ 10. .
№ 11.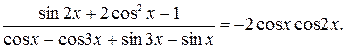 
Решений нет.