Построение первой формулы Ньютона в пакете MATHCAD
Лабораторная работа № 6
ИНТЕРПОЛИРОВАНИЕ ДЛЯ ТАБЛИЦ С ПОСТОЯННЫМ ШАГОМ. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ.
ОБРАТНОЕ ИНТЕРПОЛИРОВАНИЕ
Цель работы: изучить формулы интерполяции для таблиц с постоянным шагом; научиться решать задачи численного дифференцирования и обратного интерполирования; для функции, заданной таблично, найти приближённое значение в точках 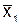 ,
, 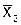 ,
, 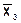 и значение производной в точке
и значение производной в точке 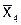 ; найти корень уравнения методом обратной интерполяции.
; найти корень уравнения методом обратной интерполяции.
Постановка задачи
1. Построить матрицу конечных разностей в среде пакета MATHCAD.
2. Написать функции в среде пакета MATHCAD, реализующие первую и вторую формулы Ньютона, первую и вторую формулы Гаусса. Найти значения функции в узловых точках, используя полученные функции.
3. Вычислить значения в заданных точках 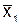 ,
, 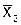 ,
, 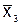 в среде MATHCAD.
в среде MATHCAD.
4. Построить график интерполяционного полинома.
5. Проверить полученные значения, используя встроенные функции пакета MATHCAD.
Содержание отчета
1. Постановка задачи.
2. Теоретические сведения.
3. Листинги счета на ЭВМ.
4. Выводы.
Теоретические сведения
Конечные разности. Пусть известны значения некоторой функции 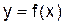 для равноотстоящих значений аргумента
для равноотстоящих значений аргумента 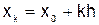
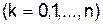 . Конечными разностями первого порядка называются следующие величины:
. Конечными разностями первого порядка называются следующие величины:
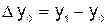 ;
; 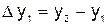 ; …;
; …; 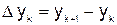 ; … .
; … .
Аналогично определяются конечные разности второго порядка:
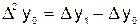 ;
; 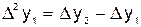 ; …;
; …; 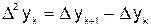 ; …
; …
и т.д.
Конечные разности 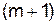 -го порядка выражаем через конечные разности
-го порядка выражаем через конечные разности 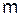 -го порядка:
-го порядка: 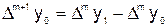 ;
; 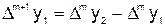 ; …;
; …; 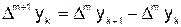 ; … .
; … .
Вычисление конечных разностей можно оформить в виде
табл. 6.1, которая называется диагональной таблицей конечных разностей.
Таблица 6.1
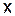 | 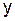 | 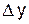 | 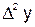 | 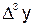 | 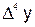 | |
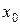 | 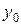 | |||||
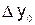 | ||||||
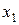 | 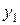 | 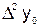 | ||||
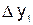 | 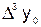 | |||||
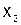 | 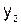 | 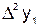 | 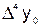 | |||
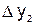 | 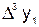 | |||||
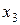 | 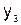 | 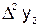 | ||||
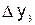 | ||||||
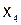 | 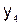 | |||||
Первая интерполяционная формула Ньютона. Интерполяционный полином Ньютона – форма записи интерполяционного полинома Pn(x), которая допускает уточнения результатов интерполирования последовательным прибавлением новых узлов.
Первая интерполяционная формула Ньютона имеет вид
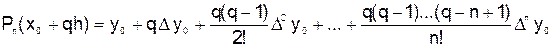 ,
,
где 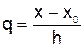 .
.
Формула используется для интерполирования в точках 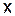 , близких к началу таблицы
, близких к началу таблицы 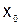 , поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей.
, поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей.
Погрешность первой интерполяционной формулы Ньютона записывается в виде
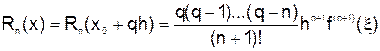 ,
,
где 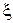 – некоторая точка интервала, содержащего узлы интерполяции.
– некоторая точка интервала, содержащего узлы интерполяции.
Вторая интерполяционная формула Ньютона. Пусть точка интерполирования 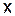 лежит вблизи конечной точки таблицы
лежит вблизи конечной точки таблицы 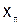 . В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона
. В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона
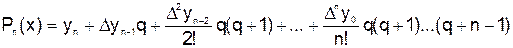 ,
,
где 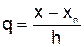 .
.
Вторая интерполяционная формула Ньютона содержит конечные разности, расположенные в нижней косой строке таблицы конечных разностей.
Погрешность второй формулы
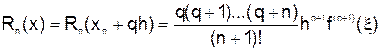 ,
,
где 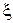 – некоторая точка интервала, содержащего узлы интерполяции
– некоторая точка интервала, содержащего узлы интерполяции 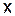 .
.
Интерполяционная формула Гаусса. Пусть точка интерполирования 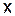 лежит в середине таблицы между узлами интерполяции
лежит в середине таблицы между узлами интерполяции 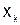 и
и 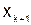 , т.е.
, т.е. 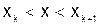 . В этом случае для интерполирования применяется интерполяционная формула Гаусса
. В этом случае для интерполирования применяется интерполяционная формула Гаусса
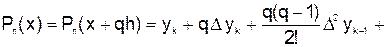
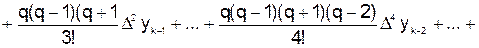
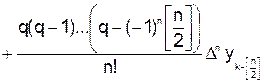 ,
,
где 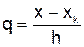 ;
; 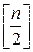 – целая часть числа
– целая часть числа 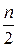 .
.
Погрешность интерполяционной формулы Гаусса имеет вид
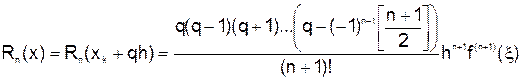 ,
,
где 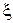 – некоторая точка интервала, содержащего узлы интерполирования.
– некоторая точка интервала, содержащего узлы интерполирования.
Для нахождения корня уравнения 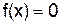 методом обратной интерполяции нужно рассмотреть функцию
методом обратной интерполяции нужно рассмотреть функцию 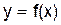 и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.
и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.
Пример выполнения заданий
Построение первой формулы Ньютона в пакете MATHCAD.
Пример функции для построения матрицы конечных разностей:
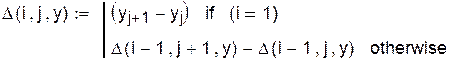
Первая формула Ньютона может иметь вид
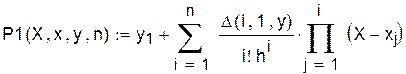
Формулу Гаусса можно реализовать следующим образом:
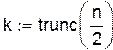

где x, y – табличные значения; X – точка интерполяции; n – количество узловых точек.
Варианты заданий
| Номер варианта | Функция | Точки интерполяции | Номер варианта | Функция | Точки интерполяции | |
| А | А | |||||
| Б | Г | |||||
| В | Б | |||||
| А | Д | |||||
| Г | Г | |||||
| В | А | |||||
| Б | Д | |||||
| Д | Б | |||||
| А | В | |||||
| Г | Г | |||||
| В | Б | |||||
| Д | А | |||||
| Б | В | |||||
| В | Г | |||||
| Д | Д |
Точки интерполяции
| № п/п | 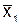 | 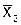 | 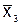 | 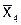 | № п/п | 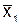 | 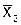 | 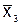 | 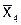 | |
| 0,01 | 0,52 | 0,89 | 0,02 | 0,04 | 0,54 | 0,89 | 0,86 | |||
| 0,04 | 0,46 | 0,87 | 0,88 | 0,03 | 0,43 | 0,86 | 0,02 | |||
| 0,05 | 0,41 | 0,86 | 0,03 | 0,02 | 0,43 | 0,87 | 0,86 | |||
| 0,02 | 0,32 | 0,89 | 0,87 | 0,03 | 0,42 | 0,88 | 0,02 | |||
| 0,01 | 0,45 | 0,88 | 0,03 | 0,05 | 0,43 | 0,87 | 0,89 |

