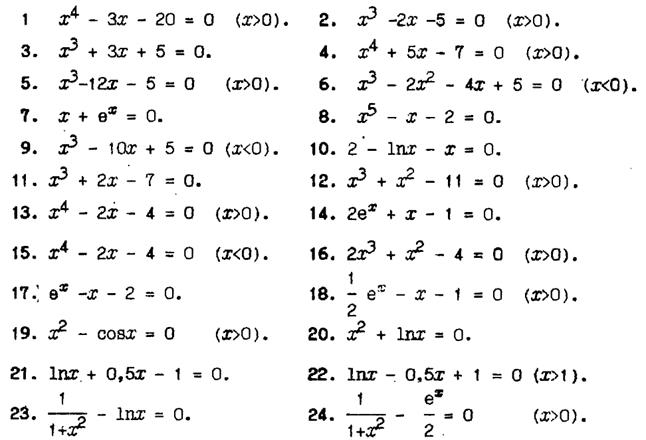Метод последовательных приближений

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ

МЕТОД ИТЕРАЦИЙ

Нахождение корней уравнения — это одна из древнейших математических проблем, которая не потеряла своей остроты и в наши дни: она часто встречается в самых разнообразных областях науки и техники.

В общем случае, если имеется некоторая функция F(х), то бывает необходимо найти такие значения аргумента х, для которых

F(х) = 0. (1)

Функция F(x) может быть алгебраической или трансцендентной; мы обычно будем предполагать, что она дифференцируема.

В общем случае функции, которые мы будем рассматривать, не имеют аналитических формул для своих корней в противоположность, например, квадратному уравнению. Поэтому приходится пользоваться приближенными методами нахождения корней, которые в основном состоят из двух этапов:

1. Отыскание приближенного значения корня.

2. Уточнение приближенного значения до некоторой заданной степени точности.

Очень часто приближенное значение корня бывает известно из физических соображений, в других случаях можно использовать графические методы. Кроме того, существуют специальные методы нахождения приближенного корня для того практически важного случая, когда F(х) является полиномом.

Здесь рассмотрены различные методы, относящиеся ко второму этапу — уточнению первоначального приближения. Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения, называется методом итераций. Каждый шаг в таком методе называется итерацией. Если при последовательных итерациях получаются значения, которые все ближе и ближе приближаются к истинному значению корня, то говорят, что метод итераций сходится.

Сейчас мы рассмотрим несколько различных методов итераций для решения уравнений и исследуем, при каких условиях эти методы сходятся.

МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ

Предположим, что (1) переписано в виде

x = f(x). (.2)

Это преобразование можно сделать различными путями.

Например, если

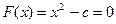
где с ≥ 0, то можно прибавить к правой и к левой частям х

(3)

или можно разделить все выражение на x; и получить

(4)

Наконец, можно преобразовать уравнение к следующему виду:

Очевидно, что значения х, являющиеся корнями этого уравнения, равны

Пусть х₀ будет исходным приближенным значением корня уравнения (2). Тогда в качестве следующего приближения примем

В качестве следующего приближения возьмем

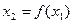
Продолжая этот процесс дальше, в качестве n-го приближения необходимо положить

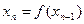(5)

Основной вопрос, который необходимо выяснить при пользовании этим методом, — сходится ли х_п крешению уравнения (2) при возрастании n?

Мы выведем сейчас достаточные условия для сходимости метода; иными словами, выведем условия, которые являются гарантией того, что последовательные значения x_n будут приближаться к решению уравнения (2). Необходимо отметить, что эти условия не являются необходимыми, так как существуют функции, для которых эти условия не выполняются, но для которых, тем не менее, с помощью (5) можно найти их решения.

Рассмотрим сначала геометрическое представление процесса. При решении уравнения (2) отыскивается точка пересечения кривой и прямой у = х. Рассмотрим рис. 1, на котором изображена некоторая кривая у = f(х). Кривая эта может представлять собой какую угодно функцию, но для нас сейчас важно то обстоятельство, что производная этой кривой положительна и меньше 1, т. е. 0 < f'(х) < 1. Пусть x = a — значение х в точке пересечения; тогда а является корнем этого уравнения. Естественно, приступая к решению задачи, мы не знаем значения корня.

Зададимся некоторым х₀. Значение x₁ равно f(х₀). Так как ОА на рис. 1 равно f(х₀), то найти х₁ можно следующим образом: проведем через точку А горизонтальную линию до пересечения с прямой у = х в точке В, как показано на рисунке. Значение х₂ = f(х₁) можно найти, проведя через точку B вертикальную линию до пересечения с кривой у = f(х)). При этом мы получаем отрезок ОС, равный f(х₁), и проводя через точку С горизонтальную линию до пересечения с прямой у = х, получаем х₂. Процесс продолжается в том же порядке и дальше; на рисунке последовательность операций показана стрелками.

На рисунке видно, как последовательные значения х сходятся к x = а. Важно помнить, что для рассмотрения мы взяли кривую, производная которой положительна и меньше 1.

Рис. 1. Геометрическое представление метода последовательных приближений для 0 < f'(х) < 1.

Рассмотрим теперь другую кривую у = f(х), производная которой отрицательна, но меньше 1 по абсолютной величине. Этот случай изображен на рис. 2. Последовательные операции вычисления решения этого уравнения снова изображены стрелками; приближения опять сходятся к решению х = а. В противоположность тому, что имело место для функции с положительной производной (см. рис. 1), на этот раз каждое последующее приближение находится с противоположной стороны от х = а. Для функции с положительной производной все последовательные приближения находились с одной стороны от истинного значения корня.

Наконец, рассмотрим случаи, когда производная функции больше 1 (рис. 3) и меньше -1 (рис. 4). В обоих случаях метод расходится. Каждое последующее значение х отстоит дальше от истинного значения корня, чем предшествующее. Поэтому кажется обоснованным предположение, что итерации по формуле (5) сходятся при условии, что производная f'(x) меньше 1 по абсолютной величине.

Рис. 2. Геометрическое представление метода последовательных приближений для 0 > f'(х) > -1.

Действительно, именно так и обстоит дело, и сейчас мы в этом убедимся с помощью элементарных выкладок. Заметим, что

а = f(а),

x_п = f (x_n-1),

так что

х_п - а = f(x_n-1) - f(а).

Умножая правую часть на и используя теорему о среднем значении¹), получаем

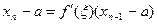
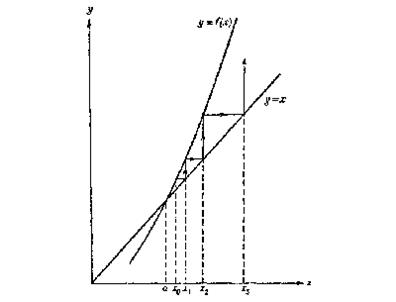
Рис. 3. Геометрическое представление метода последовательных приближений для f'(х) > 1.

Теперь пусть m будет максимальным значением f'(х) во всем рассматриваемом интервале, т. е. в интервале, включающем в себя х₀ , х₁, х₂, ..., х_п, а.. Тогда .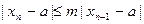

________

¹) Теорема о среднем значении утверждает, что если производная функции непрерывна на некотором интервале а, b, то тангенс угла наклона хорды, проведенной между а и b, т. е

равен производной функции в некоторой промежуточной точке, лежащей между а и b.

Таким же образом получаем

и поэтому

.

Рис. 4. Геометрическое представление метода последовательных приближений для f'(х) < -1.

Продолжая те же выкладки, получаем

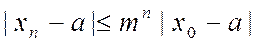. (6)

Очевидно, что, если во всем интервале n <1, то независимо от выбора начального значения х₀ с возрастанием п правая часть неравенства становится малой и х_п сходится к а.

С другой стороны, для случая | f'(x) | > 1 величина | х_п — а |неограниченно возрастает с ростом п.

Таким образом, если | f'(x) | < 1, то процесс сходится, если же | f'(x) | > 1, то процесс расходится. Обратите внимание, что неравенства должны выполняться при всех значениях х_п, вычисляемых в ходе решения задачи.

Что произойдет в случае, когда производная f'(х) в некоторых точках х_i меньше, а в других точках х_j больше 1 по абсолютной величине? Точного ответа на этот вопрос не существует, процесс иногда сходится, иногда расходится.

Вообще говоря, хотя для всякого уравнения можно найти большое количество соответствующих ему функций f(х) в выражении (2), нужно с большой осторожностью подходить к их конкретному выбору, так как от него зависит сходимость метода итераций.

ЗАДАНИЕ Решить методом итераций