Электр схемалар. Түрлері

Электрлік схема – бұл идеалды элементтердің шартты белгілерінен тұратын электрлік тізбектің графикалық бейнесі. Схемада электр энергияның көздері ЭҚК көзі түрінде (1.2 сурет) және тоқ көзі түрінде ( 1.3 сурет) келтіріледі.

i(t)

эл. тізбегі

+

-

e(t)

i(t)

эл. тізбегі

J(t)

+

-

ЭҚК көзі – сыртқы тізбекке берілетін токтың шамасы қыспақтардың арасындағы кернеуден тәуелсіз болатын элемент. ЭҚК идеалды көзінің ішкі кедергісі нөлге тең. Тоқ көзі – тоғы қоректендіретін тізбектің параметрлерінен тәуелді болмайтын элемент. Тоқ көзінің ішкі кедергісі шексіз үлкен болады. Тоқ көзінің сыртқы сипаттамасы 1.5 суретінде, ал ЭҚК көзінің сыртқы сипаттамасы 1.6 суретінде көрсетілген.

Тоқ көзін ЭҚК көзіне баламалы ауыстыру

7 Тізбектің топологиясы. Граф. Подграфтар.

Электромагниттік процестері кернеулік және ток түсініктерінің көмегімен сипатталатын, электр тогын жүргізуге арналған қондырғылар жиынын электр тізбегі деп атайды. Жалпы жағдайда, электр тізбегі ток көзі мен қабылдағышты байланыстыратын электр энергиясының көзі мен қабылдағыштардан және аралық бөлімдерден тұрады. Электр тізбегіндегі электромагниттік процестерді ток, кернеу, э.қ.к-і, кедергі, индуктивтік, сыйымдылық түсініктерінің көмегімен сипаттауға болады.

Электр тізбегі өзінде орналасқан элементтерді және олардың байланысу тәсілдерін сипаттайды. Электр тізбегінің элементтерінің байланысы схемада анық көрінеді. Ал электр тізбегінің топологиясында тізбектегі элементтер мен олардың мағынасы, қасиеті орналасуы маңызды емес. Мысалы, екі түрлі электр тізбегін қарастырайық және түйін, тармақ деген екі ұғым енгізейік.

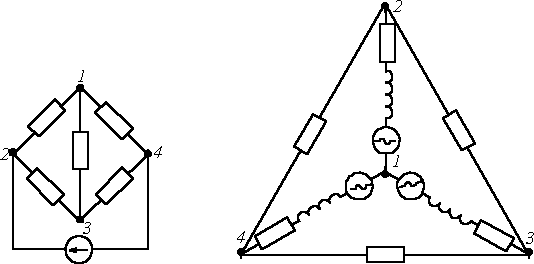
1,2-сурет.

Тармақ – тек бір ток жүретін тізбек бөлігі. Ал түйін дегеніміз үш немесе одан көп, элементтері бар, өткізгіштер қосылған орын.

Берілген схемалар формасы жағынан да, мағынасы жағынан да әр түрлі, бірақ екі тізбек те бірдей жалғанған алты тармақтан, төрт түйіннен тұрады. Сондықтан тармақтардың байланыс топологиясы ұқсас.

Электр тізбегінің топологиялық қасиеті тармақтарда орналасқан элементтердің түрі мен қасиетінен тәуелсіз. Сондықтан схемада берілген тармақтарды жай сызықпен белгілеуге болады. Егер 1 және 2 схемалардағы тармақтарды жай сызықпен алмастырсақ, 3-суреттегідей геометриялық фигура пайда болады.

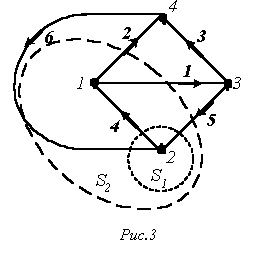Электр тізбегінің барлық тармақтарын жай сызықпен белгілеп, шын токтардың бағыты белгіленген күйдегі схеманың сұлбасы граф деп аталады.

Жай сызықпен белгіленген схеманың тармақтары граф тармақтары деп аталады. Әрбір екі тармақтың шекарасындағы нүкте граф түйіні деп аталады. Әр тармақтың өз бағыты болады. Подграф дегеніміз графтың бір тармағы немесе графтың кез келген бір түйіні. Электр тізбектері теориясында мына подграфтардың маңызы зор:

1. Жол – графтың бөлігінде әр тармақ пен түйін бір рет ғана кездесуі және осы жиынтықтың реттелген болуы. Мысалы 3–суретте 2-6-5, 4-5, 3-6-4, 1 тармақтары 1 мен 3 түйіндердің арасындағы жолдарды көрсетеді. Жол – үздіксіз өтетін тармақтардың жиынтығы.

2. Контур – бір түйіннің бастапқы және соңғы түйін болып табылуы. Мысалы төмендегі суретте: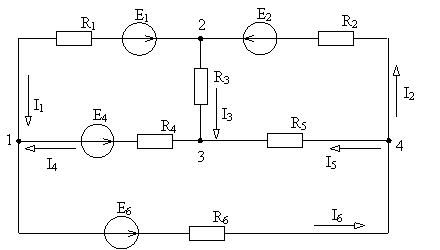

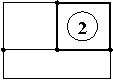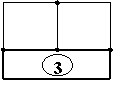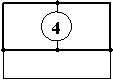
3. Тал – графтың бөлігінде барлық түйіндердің болып, бір де бір контурдың болмауы.

3-суреттегі граф үшін осындай талдар бола алады:

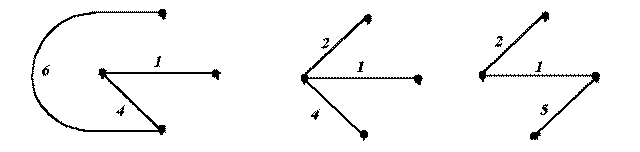
4. Байланыс тармақтары – талды бастапқы графқа толтыратын тармақтар. Егер графта m түйін мен n тармақ болса, онда кез келген талдың тармақ саны d=m-1, ал графтың байланыс тармақтарының саны c=n-(m-1)=n-m+1.

5. Граф қисыны – екі жеке подграфқа бөлетін көптеген тармақтар жиыны. 3-суреттегі мысалы S₁ және S₂. Осыдан 6-4-5, 6-2-1-5 тармақтары арқылы құралған граф қисынын аламыз.

Тал түсінігіне басты контур және басты қисын түсініктері байланысты:

ü Басты контур – талдың тармақтарынан және бір байланыс тармағынан тұратын контур;

ü Басты қисын – байланыс тармақтарынан және бір ғана талдың тармағынан тұратын қисын.