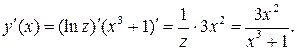Степеневий ряд. Радіус збіжності степеневого ряду

Ряд виду

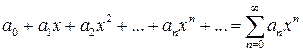(8)

називається степеневим рядом. Числа 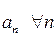називаються коефіцієнтами ряду (8).

Сумою ряду (8) є деяка функція 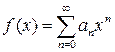, яка визначена в області збіжності цього ряду. Якщо ряд (8) збігається не при всіх значеннях х (і не лише за х=0), тоді 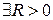, що ряд абсолютно збігається при 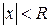і розбігається при 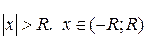називається інтервалом збіжності степеневого ряду. Число R називається його радіусом збіжності, який визначається за формулою Даламбера:

. (9)

При 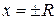(на кінцях інтервалу збіжності) ряд (8) може збігатися або розбігатися (потрібні додаткові дослідження ряду).

Приклад 1. Дослідити ряд .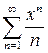

За формулою Даламбера маємо: 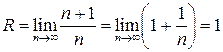. Отже, даний ряд збігається при .

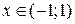Дослідимо поведінку ряду на кінцях інтервалу збіжності. При отримуємо гармонічний ряд , який розбігається, а при ряд 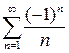, який за ознакою Лейбніца, збігається. У результаті, степеневий ряд 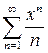збігається при .

Приклад 2. Дослідити ряд .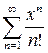

Оскільки 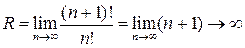, тоді даний ряд збігається абсолютно на всій числовій прямій: .

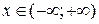Зауваження. Якщо 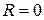, тоді степеневий ряд розбігається на всій числовій прямій за виключенням лише точки .

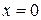6. Похідна функції. Її геометричний та фізичний зміст. Диференціал функції. Правила диференціювання

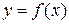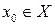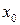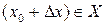Нехай на деякій множині Х визначена функція . Візьмемо будь-яку точку і задамо аргументу х у точці довільний приріст так, щоб точка . Тоді функція 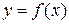також отримає приріст .

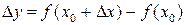Похідною функції 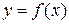у точці 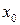називається границя при 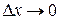відношення приросту функції в цій точці до приросту аргументу:

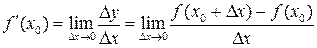. (10)

Приклад 1. Знайти похідну функції 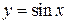у точці .

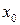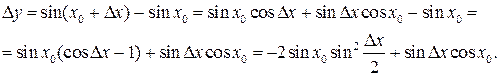
Тоді, згідно з означенням похідної:

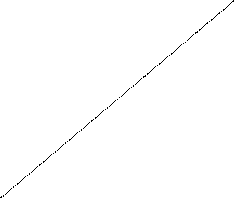
Розглянемо графік функції 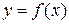. Візьмемо на ньому (Рис. 1) точку М з координатами (х,у) і другу точку Р на цьому ж графіку з координатами ( ). Проведемо січну МР і позначимо через φ, кут утворений січною з додатнім напрямом осі Ох.

у

Т

Р у=f(x)

М φ

φ Q

A B

О х х+Δ х х

α

Рис. 1

Крім того, через точку М проведемо пряму МQ паралельну осі Ох.

Як видно з Рис.1,

бо .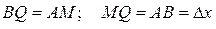

Отже, .

Якщо тепер приріст буде прямувати до нуля, тобто точка Р буде прямувати до М уздовж кривої 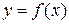, то кут φ прямуватиме до кута α, утвореного дотичною МТ з додатним напрямом осі Ох. А тому

.

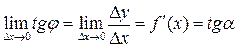Читається так: похідна в даній точці х дорівнює тангенсові кута, утвореного дотичною до кривої в точці М(х,у) з додатнім напрямом осі Ох, тобто дорівнює кутовому коефіцієнту цієї дотичної (геометричний зміст похідної).

Знаючи похідну функції 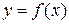, можна легко побудувати дотичну до кривої, що є графіком даної функції.

Нехай функція 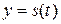описує закон руху матеріальної точки М, тобто у – це шлях, який пройшла точка за час t. Тоді 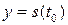–шлях, який пройшла точка М за час 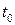. За проміжок часу 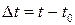точка М пройде шлях .

0 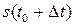s

Тоді границя 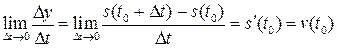визначає миттєву швидкість 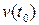матеріальної точки в момент часу 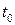(фізичний зміст похідної).

Якщо функція 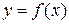має в точці 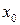скінченну похідну, тоді кажуть, що вона диференційовна в цій точці і неперервна в ній, причому , де величини 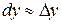і називаються диференціалами функції 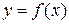і незалежної змінної х, відповідно. Таким чином, знайти диференціал функції 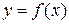у деякій точці х означає знайти похідну в цій точці і домножити її на 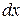, тобто:

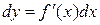. (12)

Якщо функці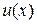ї і 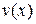диференційовні в точці х, тоді справедливі такі формули диференціювання:

(13)

Якщо складена функція , де 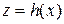, має похідну, тоді має місце така формула:

, (14)

Нехай функція 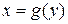є оберненою функцією для функції 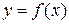, яка має похідну в точці 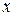, тоді справедлива така формула:

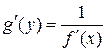. (15)

Наведемо таблицю похідних основних елементарних функцій:

1.

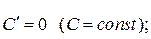
2. 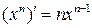( степенева функція );

3. 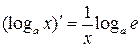( логарифмічна функція), ;

4. 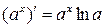( показникова функція), ;

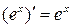5. (тригонометричні функції);

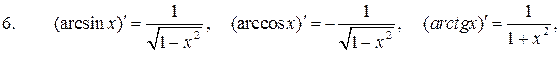
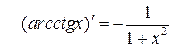
(обернені тригонометричні функції).

Приклад 2. Обчислити похідну функції .

Представимо цю складену функцію за допомогою двох простих

.

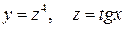Тоді за правилом диференціювання складених функцій (14) матимемо

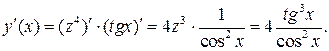
Приклад 3. Обчислити похідну функції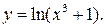

Представимо цю складену функцію за допомогою двох простих

.

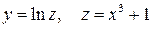Тоді за правилом диференціювання складених функцій (14) матимемо