Исходные данные к задаче представлены в таблице 1. Учебно-методическое пособие

Учебно-методическое пособие

к выполнению расчетно-проектировочной работы «Методы преобразования»

для студентов всех профилей обучения

очной и очно-заочной форм обучения

Уфа 2010

Пособие предназначено для самостоятельной работы студентов при выполнении расчетно-графической работы «Методы преобразования». Пособие содержит варианты заданий и примеры выполнения задач. Рекомендуется для студентов очной и заочной форм обучения при изучении дисциплины «Инженерная графика»

Составитель Алушкина Т.В., доц. канд. техн. наук

Рецензенты:

© Уфимский государственный нефтяной технический университет, 2010

Расчетно-графическая работа № 1

Часть 2. Методы преобразования

Цель работы:

Освоить методологию способов преобразования комплексного чертежа и основные приемы работы при решении задач на эпюре Монжа.

Для выполнения работы необходимо знать основные положения начертательной геометрии:

-понятия точки, прямой, плоскости и способы их проецирования;

-теоремы о принадлежности: точки и прямой плоскости, точки прямой;

-взаимное положение прямых, плоскостей, прямой и плоскости;

-способы преобразования комплексного чертежа – способ вращения вокруг проецирующей прямой, способ плоскопараллельного перемещения, способ вращения вокруг прямой уровня, способ замены плоскостей проекций и способ совмещения.

Работа состоит из пяти комплексных задач, при решении которых необходимо уметь применять перечисленные методы применительно к рассматриваемой ситуации.

Работа выполняется на формате А4. Каждая из задач должна быть размещена на отдельном формате А4, основная надпись – штамп по форме 2а (15×185). Делается титульный лист (Приложение А). Работу необходимо скрепить. Исходные данные, рамка, штамп выполнить простым карандашом в соответствии с ГОСТами ЕСКД. Дополнительные построения выполнять цветными карандашами или пастой (синей, зеленой и т.д.), результат построений выделить красным цветом.

Все надписи на чертеже выполняются простым карандашом шрифтом №5, индексы – шрифт №3,5.

Исходные данные к решению задач представлены в таблице 1.

Таблица 1

№ вар-та

А

B

C

D

E

F

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

Продолжение таблицы 1

№ вар-та

А

B

C

D

E

F

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

X

Продолжение таблицы 1

№ вар-та

А

B

C

D

E

F

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

X

Задача № 1.

Условие задачи:

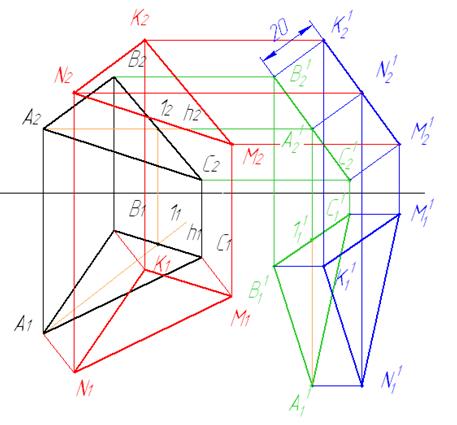
Построить плоскость ΔKMN, равную и параллельную плоскости ΔАВС и отстоящую от нее на расстоянии 20 мм. Определить видимость. Задачу решить методом плоскопараллельного перемещения.

Исходные данные к задаче представлены в таблице 1.

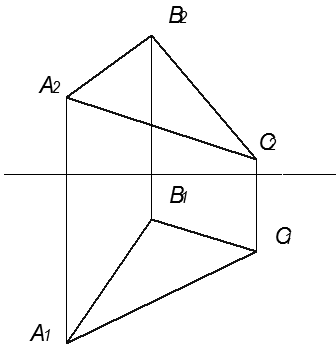
Рисунок 1

Решение:

При использовании метода плоскопараллельного перемещения необходимо помнить положения:

1) Ось вращения отсутствует;

2) Меняется положение фигуры в пространстве;

На эпюре эти правила выражаются следующими свойствами:

-одна проекция меняет свое положение, не меняя размеров;

-вторая проекция перемещается по прямым, параллельным оси Х.

Алгоритм решения задачи следующий:

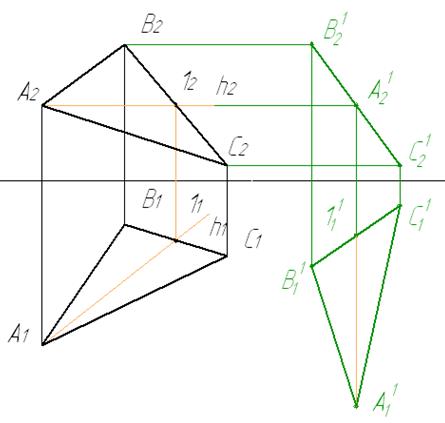
1 Проводим главную линию плоскости (линию уровня), например, горизонталь

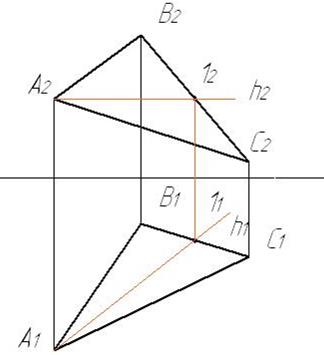
2 Перемещаем горизонтальную проекцию треугольника А₁В₁С₁ так, чтобы горизонталь h₁ расположить перпендикулярно оси Х. Проводим отрезок А¹₁ 1¹₁ , и относительно имеющихся точек достраиваем с помощью циркуля недостающие точки.

h₁┴ Х; А₁1₁=А¹₁1¹₁

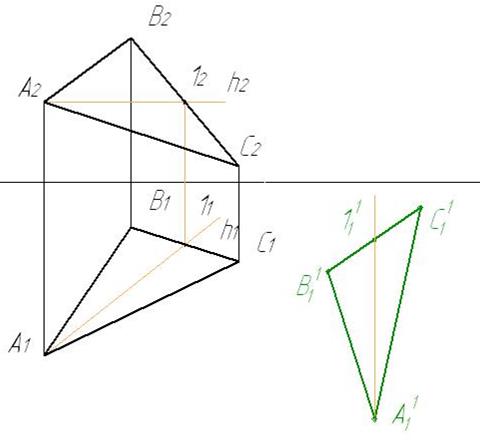
3 Достраиваем вторую проекцию треугольника АВС, для чего из соответствующих точек проводим линии связи. В результате получаем проекции проецирующей плоскости.

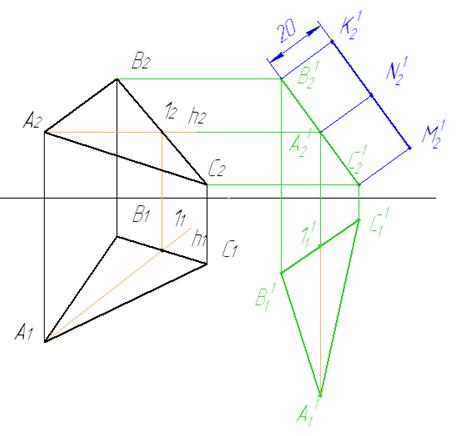
4 Восстанавливаем перпендикуляр длиной 20 мм из любой вершины треугольника и проводим отрезок K¹₂N¹₂M¹₂ равный и параллельный В¹₂А¹₂С¹₂.

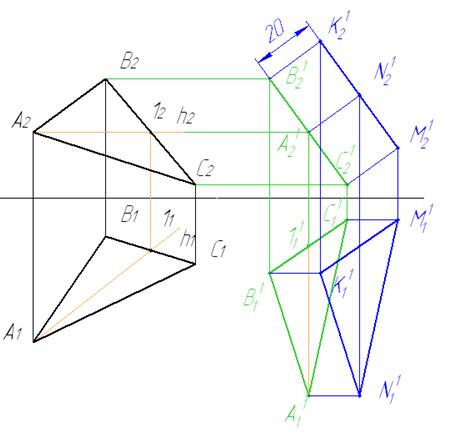
5 Достраиваем вторую проекцию треугольника K¹₁N¹₁M¹₁.

6 Используя метод плоскопараллельного перемещения переносим построенный треугольник K¹₁N¹₁M¹₁ на исходный эпюр.

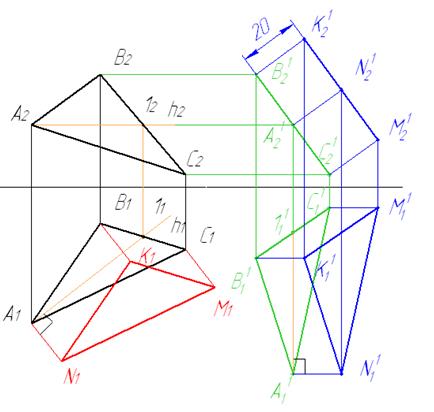
7 Достраиваем вторую проекцию

8 Определяем видимость треугольников.