Гидродинамический и тепловой пограничные слои

Для инженерной практики особый интерес представляет теплообмен между жидкостью и основным телом. Рассмотрим особенности течения и переноса теплоты в пристенном слое жидкости.

Условия «прилипания». В настоящее время в гидродинамики вязкой жидкости получила признание гипотеза о том, что частицы жидкости, непосредственно прилегающие к твердому телу, адсорбируются последним, как бы прилипают к его поверхности, то есть их скорость равна скорости тела (а если тело неподвижно, то нулю).

Этот слой «прилипшей» жидкости можно рассматривать как бесконечно тонкий слой. Гипотеза о равенстве нулю скоростей жидкости на стенке хорошо согласуются с экспериментами. Эта гипотеза справедлива до тех пор, пока газ можно считать сплошной средой. По мере увеличения разрежения газ вблизи стенки начинает проскальзывать.

Мы будем рассматривать в основном сплошные среды.

Уравнение теплоотдачи.

Так как у поверхности твердого тела имеет место тонкий слой неподвижной жидкости, то плотность теплового потока на стенке (теплоотдача) может быть определена по уравнению Фурье:

q_c = - l (¶T/¶n)_n=0,

где n – нормаль к поверхности тела.

При необходимости по известному полю температур можно определить и коэффициент теплоотдачи

a = 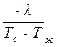(¶Т/¶n)_n=0 – уравнение теплоотдачи

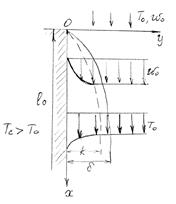
Гидродинамический пограничный слой

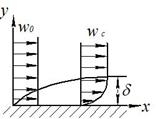
Рис. 20 Изменение скорости в гидродинамическом пограничном слое

Рассмотрим продольное обтекание плоской поверхности тела безграничным потоком жидкости. Скорость равна w₀, а температура Т₀.

При соприкосновении частиц жидкости с поверхностью тела они «прилипают» к ней. В результате в области около пластины вследствие действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости называется гидродинамическим пограничным слоем. (Теория гидродинамического пограничного слоя впервые дана в 1904 г. Л. Прандтлем).

Чем больше расстояние х от передней кромки пластины, тем толще пограничный слой, так как влияние вязкости по мере движения жидкости вдоль тела все дальше проникает в невозмущенный поток.

Для течения жидкости внутри пограничного слоя справедливо условие ¶w_х/¶у ¹ 0; вне пограничного слоя и на его внешней границе ¶w_х/¶у = 0 и w_х = w₀

Понятия «толщина пограничного слоя» и «внешняя граница пограничного слоя» довольно условны, так как резкого перехода от пограничного слоя к течению вне слоя нет. Скорость в пограничном слое по мере увеличения у асимптотически стремиться к w₀.

Поэтому под толщиной пограничного слоя d подразумевается такое расстояние от стенки, на котором скорость будет отличаться от скорости потока вдали от тела на определенную заранее заданную малую величину e << 1 (например на 1%) при у = d w_х = (1 - e)w₀.

Таким образом, при омывании тела поток жидкости как бы разделяется на 2 части: на пограничный слой и внешний поток. Во внешнем потоке преобладают силы инерции, вязкостные силы здесь не появляются. Напротив, в пограничном слое силы вязкости и инерции соизмеримы.

Соотношение сил инерции и сил вязкости характеризуется числом Рейнольдса:

,

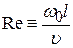где w₀ – скорость невозмущенного потока; u - кинематическая вязкости (м²/с); l – масштаб продольной координаты.

Таким образом, теория пограничного слоя приобретает характер метода упрощения математической формулировки краевой задачи и связанной с этим возможности решения.

Тепловой пограничный слой

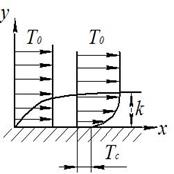
Аналогично понятию гидродинамического пограничного слоя Г.Н. Кружилин ввел понятие теплового пограничного слоя. Это слой жидкости у стенки, в пределах которой температура изменяется от значения, равного температуре стенки Т₀, до значения, равного температуре жидкости вдали от тела. Для области внутри теплового пограничного слоя справедливо условие ¶Т/¶у ¹ 0, а на внешней границе и вне его ¶Т/¶у = 0 и Т = Т₀

Таким образом, все изменения температуры жидкости сосредотачивается в сравнительно тонком слое, непосредственно прилегающем к поверхности тела.

Своеобразно строиться пограничный слой в случае свободного теплового течения, вызванного разностью плотностей более и менее нагретых частиц жидкости. Данное ранее определение пограничных слоев остается справедливым и для свободного движения. Однако во многих случаях скорость вдали от тела, у которого возникло свободное движение, равное нулю.

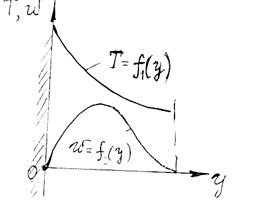
Рис. 22

На рис. 22 приведено примерное распределение температур и скоростей в определенном сечении свободного потока у горячего тела.

В данном случае толщины теплового и гидродинамических слоев могут не совпадать.

Форма и размеры поверхности теплообмена существенно влияют на теплоотдачу. В зависимости от этих факторов может резко измениться характер обтекания поверхности, по-иному строиться пограничный слой.

Известно, что имеется два основных режима течения жидкости: ламинарный и турбулентный. При ламинарном режиме частицы жидкости движутся без перемешивания, слоисто.

Турбулентный перенос теплоты и количества движения

Турбулентное течение существенно отличается от ламинарного. На рис. покажем осциллограммы колебаний скорости в определенной неподвижной точке турбулентного потока, имеющего неизменную среднюю скорость.

Скорость пульсирует около некоторого среднего во времени значения. Причем изменяется не только абсолютная величина w (которая показана на рисунке), но и направление мгновенной скорости. Отключение мгновенной скорости w от средней во времени 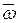называется пульсациями скорости или пульсационными скоростями w¢. При этом:

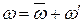
Таким образом, турбулентное движение состоит как бы из регулярного течения, которое описывается осредненными скоростями, и из наложенного на него хаотического пульсационного течения.

При пульсациях скорости происходит перенос механической энергии. Если в потоке имеет место разность температур, то пульсация скорости приводят и к переносу теплоты, вследствие чего возникают пульсации температуры. Температура в определенной точке турбулентного потока колеблется около некоторого среднего во времени значения 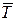. Пульсация температуры связана Т¢ связана с Т и 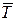уравнением:

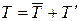
Таким образом, турбулентное течение, строго говоря, является нестационарным процессом. Однако есл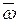и и 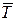не изменяются, то движение при турбулентном – неупорядоченно, хаотично, направление и величина скорости отдельных частиц беспрестанно меняется. Эти режимы течения наблюдаются и в пограничном слое. В дальнейшем мы убедимся, что теплоотдача существенно зависит от режима течения.

Подобие и моделирование процессов конвективного теплообмена

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Аналитическое решение полной системы уравнений затруднительно. Поэтому большое значение приобретает экспериментальные исследования. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.

Для исследования влияния на процесс какой-либо одной величины остальные нужно сохранять неизменными, что не всегда возможно из-за большого числа переменных. Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем число комплексов будет меньше числа величин, из которых составлены комплексы. Полученные безразмерные комплексы можно рассматривать как новые переменные.

Кроме того, новые безразмерные переменные отражают влияние не только отдельных факторов, но и их совокупности, что позволяет легче определить физические связи в процессе.

Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому.

Приведение математической формулировки краевой

задачи к записи в безразмерной форме

Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны T₀ и w₀ соответственно.

Предполагаем, что физические параметры жидкости постоянны (учтем только подъемную силу, возникающую в результате зависимости плотности от температуры). Рассмотрим процесс – стационарный (Т и скорость в каждой точке жидкости не изменяется). Расположим ось ОУ нормально к поверхности тела, а ось ОХ – направлена вдоль тела и вертикальна. При этом g_х = g, а проекции вектора сил тяжести (или подъемной силы) на оси ОУ и OZ g_y = g_z = 0. Размер тела вдоль оси OZ намного больше l₀.

При принятых условиях поля температур и скоростей можно описать дифференциальными уравнениями в приближении пограничного слоя:

w_х ¶u/¶х + w_y ¶u/¶y = a ¶²u/¶y² – уравнение энергии,

(так как толщина теплового пограничного слоя k >> l, то теплопроводностью вдоль слоя пренебрегаем, то есть ¶²u/¶х² = 0), u = Т – Т₀. движение только вдоль ОХ

w_х ¶w_х/¶х + w_у ¶w_х/¶у = n ¶²w/¶у² + gbu - уравнение движения,

_{сила трения подъемн. сила}

u = Т – Т₀; здесь постоянная скорость изменения по времени w_х равна

dw_x/dt = ¶w_x/¶t + w_х ¶w_х/¶х + w_у ¶w_х/¶у + w_z ¶w_z/¶z

_{= 0, так как задача стационарная}

И связанный с ним перенос теплоты можно рассмотрим как стационарные (квазистационарные) процессы. При этом интервал времени осреднения должен быть достаточно большим по сравнению с периодом пульсации. В общем случае пульсации скорости и температуры приводят к пульсациям давления и физических свойств.

В виду математических сложностей в достаточно строгой постановке вопросы теплообмена при турбулентном течении не решены. При рассмотрении этих процессов используют понятие: степень турбулентности – отношение средней квадратичной пульсации составляющих вектора скорости в данной точке турбулентного потока к определенному значению скорости в той же точке:

,

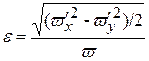где v_х¢ и v_у¢ - пульсации составляющих вектора скорости; v - осредоточенное значение скорости в точке.

Степень турбулентности влияет на интенсивность переноса количества движения и теплоты в турбулентном потоке.

На процессы переноса в турбулентном потоке оказывают влияние массы жидкости, движущиеся как единое целое, или пространственная структура турбулентности.

Представление о средних размерах турбулентных образований (масс жидкости, движущихся как единое целое) может дать величина, которая называется масштабом турбулентности.

Количество движения, относительно оси ОХ, переносимое в направлении ОY за единицу времени через единицу поверхности:

S_т = r 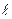²(dv_x/dy)²,

где 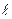– масштаб турбулентности.

То есть 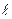– характеризует геометрическую структуру потока.

¶w_х/¶х + ¶w_у/¶у = 0 – уравнение сплошности

Граничные условия имеют вид:

1) вдали от тела (у = ¥)

u = u₀ = 0; w_х = w₀; w_у = 0

2) на поверхности тела (у = 0, 0 £ х £ 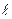₀, -¥ £ z £ +¥)

u = u_с º Т_с – Т₀ = const; w_х = w_у = w_z = 0

В уравнениях и условиях однозначности различают 3 вида величин:

Независимые переменные – х, у;

Зависимые переменные - u_, w_х, w_у;

Постоянные величины - w₀, T₀, 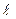₀, n, а, g, b и др. – они задаются условиями однозначности.

Таким образом, искомые зависимые переменные u_, w_х, w_у зависят от большого числа величин.

Величины, содержащиеся в уравнениях и условиях однозначности, можно сгруппировать в комплексы. Число безразмерных комплексов < числа размерных величин.

Для привидения к безразмерному виду выберем масштабы привидения. Для линейных величин выберем какой- либо характерный размер, например, длину поверхности теплообмена l₀, для скорости w₀, для температуры u_с.

Обозначим безразмерные величины:

Х = х/ 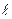₀; Y = у/ 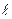₀; W_x = w_х/w₀;

W_y = w_y/w₀; Q = u/ u_с. (а)

Тогда Х 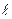₀ = х; Y 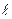₀ = у; W_xw₀ = w_х;

W_yw₀ = w_y; Qu_с = u. (б)

Подставим в уравнения согласно равенствам (б), получим:

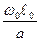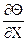(W_x + W_y 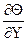) = ¶Q²/¶Y² – уравнение энергии

Здесь Ре = w_{0 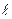0}/а – число Пекле

w_{0 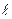0}/а = rс_рw₀u/lu/ 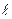₀ – здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.