Экспериментальные методы построения математических моделей
Экспериментальный статический материал (данные) получается в результате взаимодействия исследуемого объекта (процесса, явления) с некоторыми возмущениями. В результате этого взаимодействия получаем реакцию объекта. Соотношение между возмущениями и реакцией будет называться математической моделью объекта.
Получаемая на основе известных законов точных наук теоретические описания объектов есть теоретические математические модели. Например, имея электрическую схему устройства и зная соответствующие физические законы, можно записать систему дифференциальных уравнений, описывающих поведение этого устройства во времени. Это будет теоретическая математическая модель.
Методами теории экспериментов получают эмпирические модели.
Следует заметить, что любая самая точная модель будет соответствовать объекту только для конкретных условий и может изменять свою структуру и параметры в зависимости от этих условий, а также новых знаний о самом объекте.
Рассмотрим некий обобщенный объект исследования.
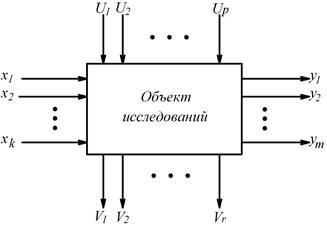
Рис. 2.9. Обобщенная структурная схема объекта измерений
Выходные величины 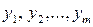 (отклики) могут быть измерены с любой, наперед заданной точностью и зависят от трех типов воздействий:
(отклики) могут быть измерены с любой, наперед заданной точностью и зависят от трех типов воздействий:
·  –это управляемые и наблюдаемые в процессе эксперимента независимые переменные (факторы);
–это управляемые и наблюдаемые в процессе эксперимента независимые переменные (факторы);
· 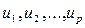 –это наблюдаемые, но неуправляемые в процессе эксперимента переменные;
–это наблюдаемые, но неуправляемые в процессе эксперимента переменные;
·  – неуправляемые и ненаблюдаемые переменные.
– неуправляемые и ненаблюдаемые переменные.
Математическая модель объекта может быть записана в виде:

где  –соответствующие векторы, причем их размерности могут не совпадать, т. е.
–соответствующие векторы, причем их размерности могут не совпадать, т. е. 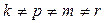 .
.
Если в ходе эксперимента регистрация контролируемых параметров параметров 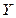 осуществляется в процессе нормального функционирования, без внесения каких-либо специальных воздействий, то эксперимент называют пассивным.
осуществляется в процессе нормального функционирования, без внесения каких-либо специальных воздействий, то эксперимент называют пассивным.
Активный эксперимент подразумевает использование специальных, целенаправленных возмущений (воздействий) Х по заранее определенной программе.
Каждый способ получение информации имеет свои недостатки и преимущества. Так, например, активный эксперимент не всегда можно осуществить на любом объекте, т. к. это может привести к аварийным ситуациям В то же время пассивный эксперимент не всегда может дать полную информацию об объекте, т. к. диапазон естественных воздействий может быть мал, а режим нормального функционирования не отвечать поставленной задаче.
Успех экспериментальных исследований существенно зависит от уровня теоретических знаний об исследуемом объекте. В свою очередь эксперимент позволяет подтвердить или опровергнуть теоретические предпосылки, т. е. является мощным средством в познании законов окружающего мира.
Любой эксперимент осуществляется в соответствии с предварительно разработанным планом, который позволяет существенно снизить затраты на проведение эксперимента и повысить достоверность результатов исследований.
Очевидно, что для каждого конкретного эксперимента может быть несколько планов, поэтому нужен критерий оптимальности, позволяющей выбрать наилучший (в определенном смысле) план. В этой связи поучителен следующий пример [2.8]:
необходимо измерить массы трех объектов (а,b,c) c помощью весов. Если измерять по обычной схеме (см. табл.2.1, где +1 означает, что обьект присутствует на весах, -1означает его отсутствие), то первое измерение будет холостым, что позволит выявить систематическую погрешность весов  . В результате последующих трех измерений получаем значение
. В результате последующих трех измерений получаем значение 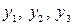 . Тогда исправленные результаты будут иметь вид:
. Тогда исправленные результаты будут иметь вид:
A=y1-y0; B= y2–y0; C=y3–y0.
Табл.2.1.
| № опыта | а | b | c | Результат |
| –1 | –1 | –1 |  | |
| +1 | –1 | –1 | 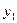 | |
| –1 | +1 | –1 |  | |
| –1 | –1 | +1 | 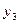 |
Полагая, что погрешности измерений отдельных измерений равны и независимы в соответствии с (2.10) можно записать
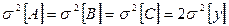 ,
,
где  - дисперсия каждого единичного измерения.
- дисперсия каждого единичного измерения.
Изменим план эксперимента, который проводим по схеме представленной в таб. 2.2. В этом случае результаты измерений будут иметь вид
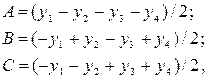
а дисперсия погрешности
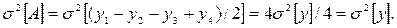
Таблица 2.2.
| № опыта | а | b | c | Результат |
| +1 | –1 | –1 | 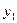 | |
| –1 | +1 | –1 |  | |
| –1 | –1 | +1 | 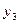 | |
| +1 | +1 | +1 |  |
Аналогично находим
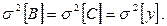
Видно, что по второму плану дисперсия погрешности результатов взвешивания вдвое меньше, хотя проведено одинаковое число опытов. Кроме того, во втором случае исключается влияние систематической составляющей погрешности 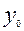 .
.
В этом примере в качестве критерия эффективности использована дисперсия случайной погрешности. Если задача эксперимента многофакторная и многооткликовая, то критерий эффективности усложняется и представляет собой функционал от всех составляющих погрешности, а задача оптимизации сводится к минимизации этого функционала.
Теория планирования эксперимента позволяет найти ответы на следующие вопросы:
· как следует организовать эксперимент, чтобы наилучшим (оптимальным) образом решить поставленную задачу,
· как следует обработать полученные результаты эксперимента, чтобы получить максимум информации об исследуемом объекте,
· как можно интерпретировать полученный результат.
Результаты эксперимента в большинстве случаев рассматривают как случайные величины поэтому основой теории планирования эксперимента является математическая статистика и теория вероятности.
Пассивные эксперименты
Особенностью пассивного эксперимента являться то, что экспериментатор не может активно воздействовать на исследуемый объект, а сам эксперимент сводится к сбору измерительной информации и ее оптимальной обработке.
Задачей пассивного эксперимента чаще всего является построение математической модели объекта. В зависимости от того, как зависят друг от друга факторы и отклики, модель может быть представлена в виде функциональной зависимости (детерминированная модель) или в виде некоторой диффузной модели, параметры которой могут быть только оценены, т.к. вычисляются на основе статистического материала.
В результате пассивного эксперимента экспериментатор получает пары чисел xi® yi ( 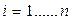 ), которым на плоскости
), которым на плоскости 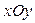 соответствуют точки (рис.2.10). Совокупность всех экспериментальных точек образует поле корреляции.
соответствуют точки (рис.2.10). Совокупность всех экспериментальных точек образует поле корреляции.
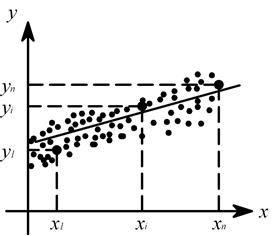
Рис. 2.10. Графическое изображение уравнения регрессии y=f(x)
Учитывая вероятностный характер полученных данных, предполагаемую зависимость  можно рассматривать только как зависимость математического ожидания
можно рассматривать только как зависимость математического ожидания 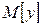 от
от 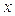 .
.
При исследовании статистически связанных зависимостей сталкиваются с двумя случаями.
В первом случае экспериментатор задает (или просто фиксирует) вполне определенным, детерминированные значения независимой переменной 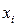 , для которых наблюдается соответствующие случайные значения
, для которых наблюдается соответствующие случайные значения 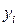 , определяемые своими статистическими характеристиками: оценкой математического ожидание и СКО. В этом случае модель называется регрессионной.
, определяемые своими статистическими характеристиками: оценкой математического ожидание и СКО. В этом случае модель называется регрессионной.
Во втором случае наблюдаемые значения 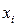 и
и 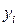 представляют собой элементы выборки, т. е. независимая переменная х сама является случайной величиной и может быть охарактеризована соответствующими оценками. Модель такого вида связи называется корреляционной.
представляют собой элементы выборки, т. е. независимая переменная х сама является случайной величиной и может быть охарактеризована соответствующими оценками. Модель такого вида связи называется корреляционной.
Пусть случайная величина y зависит от одной или нескольких неслучайных величин 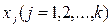 .
.
Уравнением регрессии называют функциональную зависимость математического ожидания М[y] от  , т. е.
, т. е.

а регрессивным анализом - процедуру построения уравнения регрессии и анализ его с помощью аппарата математической статистики. Он включает операции оценивания независимых параметров модели, проверки их статистической значимости, проверки адекватности полученной модели исходному статистическому материалу и т. п.
Видом (структурой) уравнения задаются заранее, исходя из физической сущности изучаемого явления, анализа накопленного статистического материала, на основании априорной информации. Поэтому непосредственной задачей регрессионного анализа является статистическое оценивание неизвестных параметров постулированной модели.
Структура модели определяется видом функции  . Если эта функция линейна относительно параметров, то говорят о линейной модели регрессии, если - нет, то модель называется нелинейной.
. Если эта функция линейна относительно параметров, то говорят о линейной модели регрессии, если - нет, то модель называется нелинейной.
Простая регрессия предполагает наличие одной независимой и одной зависимой переменной т. е.

Если число независимых переменных несколько, то регрессия называется множественной.
Методами регрессионного анализа можно решать следующие задачи:
· описание и установление возможной причинной связи между переменными;
· предсказание (экстраполяцию) зависимой переменной по значениям независимой переменной;
Рассмотрим простую регрессионную связь.
Пусть в результате однофакторного эксперимента получен статистический материал, т. е. выполнено n пар измерений единственного входного сигнала 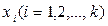 и соответствующих значений
и соответствующих значений 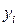 .
.
Будем искать математическую модель регрессионной связи в виде степенного полинома
 (2.43)
(2.43)
где  –искомые параметры модели.
–искомые параметры модели.
Известно [2.8], что при правильном выборе степени полинома m такая модель позволяет достаточно точно аппроксимировать истинную зависимость.
В соответствии с (2.43) для i-го результата (точки) можно записать
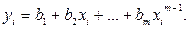 (2.44)
(2.44)
Поскольку измерение 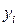 выполнены с погрешностями, то результат i-го измерения можно записать в виде
выполнены с погрешностями, то результат i-го измерения можно записать в виде

или

Используя МНК, т. е. выполняя условие

получим систему уравнений, линейную относительно искомых параметров j
 (2.45)
(2.45)
решая которую, получим оценки параметров  постулированной регрессионной модели.
постулированной регрессионной модели.
Очевидно, что полученная модель
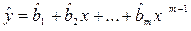 (2.46)
(2.46)
может лишь с той или иной точностью соответствовать экспериментальной совокупности  , т. к. МНК не гарантирует точного совпадения отклика, вычисленного по (2.46) и полученного экспериментально, а только утверждает, что
, т. к. МНК не гарантирует точного совпадения отклика, вычисленного по (2.46) и полученного экспериментально, а только утверждает, что 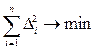 . Поэтому заключительным этапом анализа является установление адекватности полученной регрессионной модели экспериментальным данным.
. Поэтому заключительным этапом анализа является установление адекватности полученной регрессионной модели экспериментальным данным.
В качестве меры адекватности может быть использован коэффициент корреляции [2.3].
 (2.47)
(2.47)
чем ближе 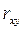 к единице, тем ближе экспериментальные точки к (2.46). Другой мерой адекватности модели является оценка дисперсии ошибки, F – критерий и др. Более подробно анализ качества полученной модели будет рассмотрен в теме «Активные эксперименты».
к единице, тем ближе экспериментальные точки к (2.46). Другой мерой адекватности модели является оценка дисперсии ошибки, F – критерий и др. Более подробно анализ качества полученной модели будет рассмотрен в теме «Активные эксперименты».
Активные эксперименты
Современная теория многофакторного эксперимента (МФЭ) зародилась в конце тридцатых годов. Именно в этот период появились первые публикации Фишера. Он предложил метод дисперсионного анализа, позволяющий получать зависимость выходной величины исследуемого объекта сразу от нескольких количественных переменных. В основе методологии МФЭ лежит системный подход, предполагающий изучение состояния объекта при одновременном изменении большого числа независимых переменных.
МФЭ позволяет решать следующие задачи:
· раскрытие механизма процесса или явления, т.е. построение математической модели в условиях неопределенности;
· выделение факторов, существенно влияющих на выходную величину;
· идентификацию объектов; т.е. определение их состояния и параметров в процессе функционирования. Решение этой задачи является предпосылкой оптимального управления объекта.
· экстраполяцию объектов в пространстве и во времени.
Рассмотрим сущность и основные понятия МФЭ. Пусть имеем однооткликовую модель т. е.
y = f (x1,x2,…,xk) (2.48)
Эта зависимость заранее неизвестна, но предполагается, что функция f(x1,…,xk) - аналитическая (гладкая) в окрестности точки  и может быть разложена в ряд Тейлора. В этом случае функция f(x1,…,xk) может быть представлена в виде полинома первой, второй и т. д. степени. Пространство, образованное факторами
и может быть разложена в ряд Тейлора. В этом случае функция f(x1,…,xk) может быть представлена в виде полинома первой, второй и т. д. степени. Пространство, образованное факторами 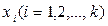 , называется факторным пространством.
, называется факторным пространством.
Каждому набору значений факторов в факторном пространстве соответствует точка, которой, в свою очередь, соответствует некоторое значение отклика y (см. рис.2.11).

Рис. 2.11. Графическое изображение двухоткликовой модели y=f(x1,x2)
Здесь x1Ox2– двухфакторное пространство. Точки 1,2,3,4 определяют четыре набора факторов. В каждой такой точке производится одно или несколько измерений отклика y1, y2, y3, y4. Полученные значения отклика используют для построения поверхности 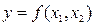 , которую называют поверхностью отклика, а наборы значений факторов (точки 1–4) образуют область эксперимента
, которую называют поверхностью отклика, а наборы значений факторов (точки 1–4) образуют область эксперимента  .
.
Для повышения точности в каждой точке факторного пространства проводят несколько независимых опытов. Такие опыты называются параллельными.
Точность аппроксимации экспериментальных точек y1, y2, y3, y4 поверхностью отклика  зависит от ряда условий, в том числе и от размеров области эксперимента
зависит от ряда условий, в том числе и от размеров области эксперимента  . При большой кривизне поверхности отклика (
. При большой кривизне поверхности отклика ( 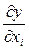 велика) с увеличением области
велика) с увеличением области  степень аппроксимирующего полинома надо увеличивать, а это усложняет эксперимент и обработку результатов. С другой стороны, эта область не может быть и слишком малой. В большинстве практических случаев она должна быть меньше области возможных значений
степень аппроксимирующего полинома надо увеличивать, а это усложняет эксперимент и обработку результатов. С другой стороны, эта область не может быть и слишком малой. В большинстве практических случаев она должна быть меньше области возможных значений 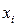 . Такую область будем называть область исследования
. Такую область будем называть область исследования  . Если
. Если 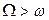 , то применяют принципы дискретного обзора факторного пространства (рис.2.12).
, то применяют принципы дискретного обзора факторного пространства (рис.2.12).
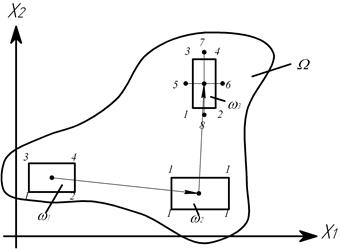
Рис.2.12. Сканирование двухфакторного пространства
В начале эксперимент ставится в некоторой области  с центром О1. Опыты проводятся в вершинах этой области. Затем, если цель эксперимента не достигнута, переходят к области
с центром О1. Опыты проводятся в вершинах этой области. Затем, если цель эксперимента не достигнута, переходят к области 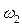 и т. д. Область
и т. д. Область  ,
,  ,
,  должны принадлежать области исследований
должны принадлежать области исследований  . В последней области
. В последней области  отклик для повышения точности измеряется в восьми точках.
отклик для повышения точности измеряется в восьми точках.
Организация эксперимента. Непосредственному проведению МФЭ предшествует подготовительная работа – предпланирование или организация эксперимента, которая состоит из:
· изучения объекта и формулировки цели исследования;
· выбора откликов;
· выбора факторов и интервалов варьирования;
· разработки экспериментальной установки, метрологического и программного обеспечения;
· составления таблицы условий и плана эксперимента.
Рассмотрим подробнее каждый из пунктов.
Формулировка цели эксперимента и выбор отклика.
Эксперимент ставится с целью получения модели объекта, которая позволяет определять количественное влияние факторов на отклик.
В общем случае задача эксперимента бывает многокритериальной, в которой необходимо искать компромиссные решения . Это обусловлено многооткликовостью реальных объектов и необходимостью получения оптимального решения.
Отклик определяется объектом исследования и задачей поставленной перед экспериментатором, но, в конечном итоге, четкое формулирование цели и выбор отклика остается за экспериментатором, т. е. здесь присутствует элемент субъективизма, однако существует ряд общих требований к отклику:
· он должен быть количественной величиной, доступной непосредственному или косвенному измерению с необходимой точностью;
· иметь простой физический смысл, т. к. в дальнейшем будет необходимо интерпретировать полученные результаты;
· обладать однозначностью, т. е. одному набору факторов должно соответствовать одно (с точностью до погрешностей опыта) значение отклика;
· быть достаточно универсальным, т. е. наиболее полно характеризовать объект, его функциональную сущность.
Выбор и кодирование факторов.
В большинстве технических приложений МФЭ факторы это независимые переменные, которые в процессе эксперимента могут изменяться по воле экспериментатора и могут быть измерены с оговоренной точностью. Следует заметить, что существует класс задач, где факторы не могут быть выражены количественно (сорт или класс продукта, квалификация оператора, препараты различных партий или заводов изготовителей и т. п.). Это относится к проведению экспериментов в области сельского хозяйства и биомедицины, экономики, социальной сферы.
На этапе предпланирования, анализируя все факторы влияющие на отклик, необходимо выбрать доминирующие, существенно влияющие на отклик. Если в ходе эксперимента не будет учтен какой-либо фактор, то это может существенно исказить результат, т. е. модель не будет отвечать критерию адекватности. С другой стороны, включение в эксперимент факторов, слабо влияющих на отклик, приводит лишним затратам, усложняет обработку результатов и делает модель излишне сложной, неудобной к применению.
В МФЭ могут быть сотни факторов, по-разному действующих на отклик. Существуют различные методики, позволяющие выделить существенные факторы. Для экспериментов с числом факторов, не превышающим пятнадцати, это осуществляется методом однофакторного эксперимента.
Все факторы изменяют в пределах 10-20% от номинальных значений. К числу значимых относят те, которые в одинаковой степени влияют отклик. Если некоторые факторы изменяют отклик на 50-100%, а большинство остальных на 10-15%, то интервал варьирования сильно действующих факторов изменяют так, чтобы отклик изменялся как от воздействия остальных.
В общем случае факторы должны отвечать требованиям:
· при изменении любого фактора остальные не должны изменяться;
· в процессе эксперимента каждый фактор может принимать два или более дискретных значений, устанавливаемых экспериментатором, поэтому они должны быть изменяемыми;
· факторы считают детерминированными, точно известными величинами, которые должны измеряться с точностью на порядок больше точности измерения отклика;
· факторы и их сочетания не должны выходить за пределы допустимых значений т. к. это может создать аварийную ситуацию. Это требование называется свойством совместимости факторов в области эксперимента  .
.
После выбора откликов и факторов приступают к разработке плана эксперимента. Планирование и обработка данных эксперимента осуществляется не в физических, а в кодированных (приведенных) переменных  , где
, где 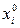 –основной уровень i–го фактора,
–основной уровень i–го фактора,  –интервал варьирования i–го фактора.
–интервал варьирования i–го фактора.

Рис.2.13. Физические и кодированные переменные
Основной уровень 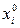 находится в середине диапазона изменения фактора
находится в середине диапазона изменения фактора 
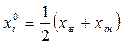 .
.
Интервал варьирования - это половина диапазона изменения фактора 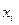
 .
.
В МФЭ наиболее часто применяют двухуровневые полные и дробные факторные эксперименты В них каждый фактор варьируется на двух уровнях 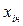 и
и 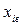 . Кодированные значения фактора
. Кодированные значения фактора  в этом случае принимают значения +1 и -1, т.е. интервал варьирования всех кодированных факторов будет один и тот же и равен 1.
в этом случае принимают значения +1 и -1, т.е. интервал варьирования всех кодированных факторов будет один и тот же и равен 1.
Для кодированных факторов в двухуровневом МФЭ необходимо знать две величины – основной уровень 
 и интервал варьирования
и интервал варьирования  . Рассмотрим как выбираются эти величины.
. Рассмотрим как выбираются эти величины.
Основной уровень  определяет центр или положение области эксперимента
определяет центр или положение области эксперимента  в факторном пространстве. Изменяя
в факторном пространстве. Изменяя  можно исследовать интересующую часть пространства. Обычно такой частью является область номинальных значений параметров.
можно исследовать интересующую часть пространства. Обычно такой частью является область номинальных значений параметров.
Интервал варьирования  определяет размер области эксперимента и существенно влияет на достоверность и информативность экспериментальных данных. С точки зрения повышения информативности необходимо увеличивать
определяет размер области эксперимента и существенно влияет на достоверность и информативность экспериментальных данных. С точки зрения повышения информативности необходимо увеличивать  . Однако увеличение
. Однако увеличение  может нарушить требование к адекватности модели. Это видно из рис. 2.14. Здесь выбрано два интервала варьирования
может нарушить требование к адекватности модели. Это видно из рис. 2.14. Здесь выбрано два интервала варьирования 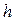 и
и 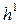 , которым соответствуют две линейные модели
, которым соответствуют две линейные модели 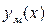 и
и 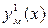 . Видно, что для интервала
. Видно, что для интервала 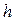 степень близости к истинной зависимости (адекватность) выше, чем для интервала
степень близости к истинной зависимости (адекватность) выше, чем для интервала 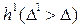 .
.

Рис. 2.14. К выбору интервала варьирования переменных
Пример. Необходимо выбрать основной уровень и интервал варьирования питающего напряжения операционного усиления. Номинальное напряжение питания  , т.е.
, т.е. 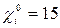 .
.
Предположим, что точность измерения напряжения соответствует «трехсигмовому» закону , т.е.
 или
или  ,
,
где  - предельное значение погрешности измерения напряжения данным прибором . Если класс точности вольтметра равен 2.5, а предельное значение шкалы - 20 В, то
- предельное значение погрешности измерения напряжения данным прибором . Если класс точности вольтметра равен 2.5, а предельное значение шкалы - 20 В, то
 ,
,
тогда
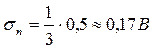 .
.
Следовательно, интервал варьирования будет равен
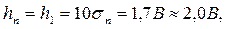
или
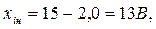
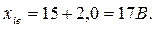
Аналогично можно вычислить значения  ,
,  и
и  для любых факторов. Результаты заносят в таблицу .
для любых факторов. Результаты заносят в таблицу .
Например, для четырехфакторного эксперимента интервалы варьирования для факторов R1, C1, R2 и Uп могут быть представлены в виде таблицы условий эксперимента.
| Величина | Фактор | |||
 |  |  | 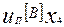 | |
Основной уровень  | ||||
Интервал варьирования  | ||||
Нижний уровень  | ||||
Верхний уровень 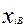 |
Практическую реализацию этих условий для электрических цепей осуществляют с помощью последовательного или параллельного подсоединения соответствующих элементов (см. рис. 2.15).
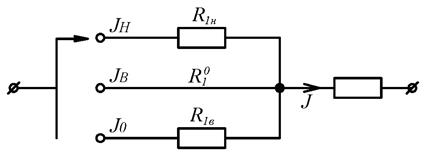
Рис. 2.15. Электрическая схема реализации варьирования переменных
МФЭ, к которым относятся полные и дробные факторные эксперименты, наиболее часто применяются для построения линейных относительно параметров полиномиальных моделей. Вид полинома структура выбирается на этапе предпланирования до проведения эксперимента, а его параметры (коэффициенты) вычисляются по полученным экспериментальным данным.
Распространение полиномиальных моделей объясняется тем, что исследуемая экспериментальными методами функция многих переменных y=f(x1,x2,…,xk) в ограниченной области эксперимента  , при некоторых допущениях, можно разложить в ряд Тейлора.
, при некоторых допущениях, можно разложить в ряд Тейлора.
Например, разложение функции двух переменных y=f(x1,x2) в окрестности центра плана x1=0, x2=0 имеет вид
 .
.
Здесь 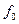 и все частные производные вычисляются для центра плана, т.е. при x1=x2=0. Вводя соответствующие обозначения, получим модель вида
и все частные производные вычисляются для центра плана, т.е. при x1=x2=0. Вводя соответствующие обозначения, получим модель вида

В практических случаях всегда можно ограничиться полиномами, включающими первые степени переменных  и их различные произведения или первые и вторые степени переменных и крайне редко более высокие степени.
и их различные произведения или первые и вторые степени переменных и крайне редко более высокие степени.
Полные и дробные факторные эксперименты, в которых каждый фактор принимает только два значения (уровня), применяются для отыскания параметров полиномиальных моделей без учета квадратов. Теоретическое уравнение такой модели, в общем случае, имеет вид:
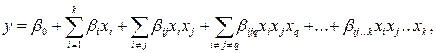 (2.50)
(2.50)
где 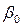 –свободный член;
–свободный член;  –коэффициенты, учитывающие влияние на отклик (эффекты) линейных членов, парных, тройных и т. д. взаимодействий факторов.
–коэффициенты, учитывающие влияние на отклик (эффекты) линейных членов, парных, тройных и т. д. взаимодействий факторов.
В силу ограниченности статистического материала, получаемого в результате эксперимента, применение МНК для определения  –коэффициентов позволяют найти только их оценки. В этом случае (2.50) запишется как
–коэффициентов позволяют найти только их оценки. В этом случае (2.50) запишется как

здесь коэффициенты  являются оценками соответствующих
являются оценками соответствующих  –коэффициентов модели (2.50), а
–коэффициентов модели (2.50), а 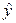 –оценка отклика у.
–оценка отклика у.
Для упрощения и формализации экспериментальной процедуры в теории планирования экспериментов применяют специальные планы.
Эксперимент, реализующий все возможные наборы факторов называется полным факторным экспериментом (ПФЭ). Тогда при варьировании всех k параметров (факторов) на двух уровнях будем иметь ПФЭ 2k. В таком эксперименте количество точек факторного пространства, в которых измеряется отклик, равно 2k.
Наборы факторов, которые реализуются в эксперименте, записываются в виде таблицы или матрицы. Эта матрица называется матрицей планирования.
Рассмотрим процедуру составления матриц планирования ПФЭ 2k для различных значений числа факторов k. Матрицу записывают в кодированных переменных xi.

Рис. 2.16. Двухфакторное пространство
Рассмотрим ПФЭ 22. Четыре набора факторов в кодированной системе координат  запишутся как: 1(–1–1), 2(+1–1), 3(–1+1),4(+1+1). В соответствии с этими значениями можно построить план, в котором каждому и набору соответствует отклик
запишутся как: 1(–1–1), 2(+1–1), 3(–1+1),4(+1+1). В соответствии с этими значениями можно построить план, в котором каждому и набору соответствует отклик  .
.
План ПФЭ 2k
| Номер набора u | Факторы | Отклик | |
 |  | ||
| –1 | –1 | Y1 | |
| +1 | –1 | Y2 | |
| –1 | +1 | Y3 | |
| +1 | +1 | Y4 |
Для этого плана матрица планирования имеет вид
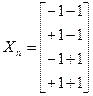
Аналогично можно записать матрицу для трех факторов.
План ПФЭ 23
| Номер набора u | Факторы | Отклик | ||
 |  | 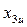 | ||
| –1 | –1 | –1 | Y1 | |
| +1 | –1 | –1 | Y2 | |
| –1 | +1 | –1 | Y3 | |
| +1 | +1 | –1 | Y4 | |
| –1 | –1 | +1 | Y5 | |
| +1 | –1 | +1 | Y6 | |
| –1 | +1 | +1 | Y7 | |
| +1 | +1 | +1 | Y8 |
Матрица планирования:


Из приведенных примеров следует общий прием построения матриц более высокого порядка. В первом столбце знак меняется поочередно, во втором - чередуется через два, а в третьем - через четыре, в четвертом - через восемь и далее по степеням двойки.
Матрицы планирования обладают тремя свойствами.
1) Свойство симметрии заключается в том, что все наборы факторов (точки плана) симметричны относительно центра плана
 ,
, 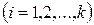 , (2.51)
, (2.51)
где u – номер опыта; N – число опытов; i - номер фактора.
Это свойство означает, что сумма элементов любого столбца матрицы планирования равна нулю
2) Свойство нормировки. Сумма квадратов элементов любого столбца равна количеству строк N, т.е.
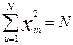 ,
, 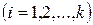 . (2.52)
. (2.52)
3) Свойство ортогональности. Сумма по членных произведений любых двух столбцов матрицы планирования равна нулю
 ,
,  . (2.53)
. (2.53)
Матрица планирования показывает: в каких точках факторного пространства надо произвести измерение отклика. Каждый u-ый опыт состоит в установке определенных значений факторов  и измерения отклика, соответствующего этому набору.
и измерения отклика, соответствующего этому набору.
Требуемые наборы кодированных факторов устанавливаются изменением соответствующих значений физических величин из таблицы условий эксперимента.
+1 соответствует 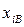 ,
,
+ соответствует 
–1 соответствует 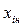 .
.
В полном факторном эксперименте опыты реализуются при всех возможных наборах уровней факторов, т. е. для двухуровнего k-факторного эксперимента опыты производятся в 2k точках факторного пространства.
На основе таких опытов можно найти 2k коэффициента уравнения регрессии. Если число факторов k  4, эффекты взаимодействия высокого порядка становятся статистически малозначимыми. Практика экспериментов показывает, что при q
4, эффекты взаимодействия высокого порядка становятся статистически малозначимыми. Практика экспериментов показывает, что при q  4 влияние сомножителей x1x2… xq на отклик у взаимно компенсируются и соответствующий коэффициент уравнения регрессии
4 влияние сомножителей x1x2… xq на отклик у взаимно компенсируются и соответствующий коэффициент уравнения регрессии 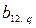 становится статистически незначимым. Этот опытный факт позволяет априорно считать, что в уравнении регрессии с большим числом факторов b–коэффициенты высоких порядков взаимодействия равны нулю. Следовательно, при большом количестве факторов можно построить такие планы, которые позволяют определить линейные эффекты факторов, эффекты их парных и редко тройных взаимодействий.
становится статистически незначимым. Этот опытный факт позволяет априорно считать, что в уравнении регрессии с большим числом факторов b–коэффициенты высоких порядков взаимодействия равны нулю. Следовательно, при большом количестве факторов можно построить такие планы, которые позволяют определить линейные эффекты факторов, эффекты их парных и редко тройных взаимодействий.
Такие процедуры позволяют существенно сократить трудоемкость проведения экспериментов.
Пример. Пусть количество факторов k=10. Тогда полный факторный эксперимент необходимо осуществить в  точек. Если ограничиться только линейными и первыми взаимодействиями, то
точек. Если ограничиться только линейными и первыми взаимодействиями, то 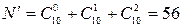 , т. е. условная трудоемкость эксперимента может быть уменьшена в
, т. е. условная трудоемкость эксперимента может быть уменьшена в  раз. Поэтому уменьшение количества определяемых коэффициентов уравнения регрессии очень актуально с точки зрения затрат на проведение эксперимента и обработки получаемых данных.
раз. Поэтому уменьшение количества определяемых коэффициентов уравнения регрессии очень актуально с точки зрения затрат на проведение эксперимента и обработки получаемых данных.
Таким образом, в экспериментах с большим количеством факторов число определяемых коэффициентов 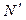 может быть значительно меньше опытных точек ПФЭ
может быть значительно меньше опытных точек ПФЭ 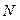 =2k. Отсюда возникает задача – построить такой план, в котором количество опытных точек будет равно количеству определяемых b–коэффициентов. Этому отвечают часть (реплики) ПФЭ 2k , кратные 2р, где р –целое положительное число.
=2k. Отсюда возникает задача – построить такой план, в котором количество опытных точек будет равно количеству определяемых b–коэффициентов. Этому отвечают часть (реплики) ПФЭ 2k , кратные 2р, где р –целое положительное число.
Такие эксперименты называются дробными факторными экспериментами ДФЭ2k-р. Количество опытных точек в ДФЭ 2k-з в 2р раз меньше, чем в ПФЭ2k . Здесь k–общее количество факторов; р–число факторов, введенных путем замены незначимых взаимодействий; (k–p)–количество исходных факторов. Так как ДФЭ2k-р является частью ПФЭ2k , то его называют дробной репликой ПФЭ. Например ДФЭ, составляющий половину ПФЭ2k обозначается ДФЭ2k и называется полурепликой ПФЭ2k . Действительно 2k-1 = 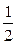 2k . ДФЭ2k-2 содержит
2k . ДФЭ2k-2 содержит 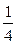 2k опытных точек и называется одной четвертой репликой ПФЭ2k .
2k опытных точек и называется одной четвертой репликой ПФЭ2k .
Обратимся к ПФЭ22 . Для него уравнение регрессии имеет вид
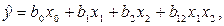
а матрица планирования
| Номер набора u | Факторы | Отклик | |||
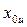 |  |  | 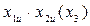 | ||
| +1 | –1 | –1 | +1 | y1 | |
| +1 | +1 | –1 | –1 | y2 | |
| +1 | –1 | +1 | –1 | y3 | |
| +1 | +1 | +1 | +1 | y4 |
Здесь 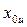 – вектор-столбец фиктивной переменной перемещенной, которая во всех опытах принимает значение +1; вектор-столбец x3= x1x2 образован путем перемножения соответствующих столбцов.
– вектор-столбец фиктивной переменной перемещенной, которая во всех опытах принимает значение +1; вектор-столбец x3= x1x2 образован путем перемножения соответствующих столбцов.
Если предположить, что эффект от взаимодействия x1x2статически незначим (  0), то в выбранных интервалах варьирования исследуемый процесс может быть описан линейной моделью, т. е. в этом случае достаточно определить три коэффициента:
0), то в выбранных интервалах варьирования исследуемый процесс может быть описан линейной моделью, т. е. в этом случае достаточно определить три коэффициента: 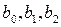 . Поскольку
. Поскольку  , то освободившийся столбец x1x2 можно использовать для построения плана ДФЭ3-1. Для этого используем новый фактор x3= x1x2. Заметим, что вектор-столбец x3, совпадает с вектором x1x2 , вектор столбец x1x2x3 , а x2 с x1x3 , т. е. соответствующие оценки коэффициентов смешиваются. Это означает, что коэффициент b1 включает в себя, кроме оценки коэффициента
, то освободившийся столбец x1x2 можно использовать для построения плана ДФЭ3-1. Для этого используем новый фактор x3= x1x2. Заметим, что вектор-столбец x3, совпадает с вектором x1x2 , вектор столбец x1x2x3 , а x2 с x1x3 , т. е. соответствующие оценки коэффициентов смешиваются. Это означает, что коэффициент b1 включает в себя, кроме оценки коэффициента  , еще и оценку коэффициента от взаимодействия x2x3 –
, еще и оценку коэффициента от взаимодействия x2x3 –  и т. д. Символически это можно записать
и т. д. Символически это можно записать
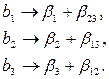
Однако мы постулировали линейную модель и, следовательно, все парные взаимодействия статистически незначимы, т. е. можно полагать, что

т. е. оценки 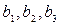 достоверны.
достоверны.
Таким образом, вместо восьми опытов для изучения влияния трех факторов достаточно осуществить всего четыре.
На основе плана, содержащего четыре строки, нельзя определить больше четырех коэффициентов уравнения регрессии. План, в котором, количество переменных (столбцов) меньше на единицу количества опытных точек (строк) называется насыщенным.
На основе плана ПФЭ 23 можно построить следующие дробные реплики:
| Число факторов | Дробные реплики | Обозначения | Число опытное | |
| Для дробной реплики | Для ПФЭ | |||
| ½ реплика от 23 | 23–1 | |||
| ½ реплика от 24 | 24–1 | |||
| ½ реплика от 25 | 25–2 | |||
| ½ реплика от 26 | 26–3 | |||
| ½ реплика от 27 | 27–4 |
Последний план – насыщенный, т. к. число факторов на единицу меньше количества строк  .
.
На основе плана ПФЭ 23 можно построить уравнение регрессии
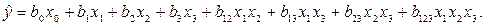
Оно содержит три парных и одно тройное взаимодействие. Если какое-либо одно взаимодействие является статистически незначимым, то строят полуреплику ДФЭ24–1. Если незначимы два взаимодействия, то строят ¼-реплику от ПФЭ 25, т. е. ДФЭ25–2 и т. д.
Построим ¼-реплику для случая, когда статистически незначимы коэффициенты  и
и 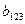 . Два дополнительных фактора
. Два дополнительных фактора 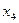 и
и 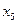 можно ввести с помощью соответствующих
можно ввести с помощью соответствующих
а) 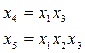 б)
б) 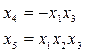 в)
в) 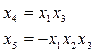 г)
г) 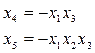
Эти соотношения называются генерирующими.
Составим план ДФЭ25–2
| Номер набора |  | 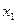 | 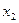 | 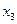 |  |  |  |  | Отклик |
| +1 | –1 | –1 | –1 | +1 | –1 | +1 | –1 | у1 | |
| +1 | +1 | –1 | –1 | –1 | +1 | +1 | +1 | у2 | |
| +1 | –1 | +1 | –1 | –1 | –1 | –1 | +1 | у3 | |
| +1 | +1 | +1 | –1 | +1 | +1 | –1 | –1 | у4 | |
| +1 | –1 | –1 | +1 | +1 | +1 | –1 | +1 | у5 | |
| +1 | +1 | –1 | +1 | –1 | –1 | –1 | –1 | у6 | |
| +1 | –1 | +1 | +1 | –1 | +1 | +1 | –1 | у7 | |
| +1 | +1 | +1 | +1 | +1 | –1 | +1 | +1 | у8 |
Для такого плана пяти факторов 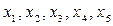 выделяют восемь точек факторного пространства, в которых необходимо построить отклик. В соответствии с ДФЭ25–2 можно построить линейную модель вида:
выделяют восемь точек факторного пространства, в которых необходимо построить отклик. В соответствии с ДФЭ25–2 можно построить линейную модель вида:

Таким образом, мы существенно сократим число опытов (8 вместо 32), однако при этом имеет место нежелательные эффекты смешивания оценок b–коэффициентов. Это означает, что при вычислении b–коэффициентов по данным МФЭ иногда получаются не оценки отдельных коэффициентов, а их различных комбинаций, например, b0 является оценкой не только  модели
модели

но и коэффициентов при квадратах факторов, т. е. квадратичных эффектов  , которые в уравнение модели не входят, но в действительности имеют место.
, которые в уравнение модели не входят, но в действительности имеют место.
Если все коэффициенты  равны нулю, то
равны нулю, то 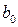 является оценкой истинного значения
является оценкой истинного значения 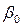 . Это можно символически записать
. Это можно символически записать


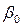 .
.
Если некоторые 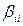 не равны нулю, то
не равны нулю, то 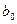 является оценкой
является оценкой 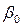 и всех, отличных от нуля
и всех, отличных от нуля 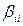

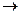
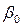
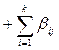
Рассмотрим подробнее эффект смешивания на примере ДФЭ23–1. Для него уравнение регрессии будет иметь вид:
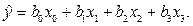
Составим для ДФЭ3–1 две структурные матрицы, отличающиеся только знаками в столбцах для 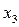 .
.
Таблица 1
| Номер набора |  | 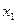 | 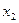 | 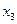 |  |  |  |  |
| +1 | –1 | –1 | +1 | +1 | –1 | –1 | +1 | |
| +1 | +1 | –1 | –1 | –1 | –1 | +1 | +1 | |
| +1 | –1 | +1 | –1 | –1 | +1 | –1 | +1 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Таблица 2
| Номер набора |  | 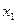 | 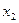 | 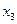 |  |  |  |  |
| +1 | –1 | –1 | –1 | +1 | +1 | +1 | –1 | |
| +1 | +1 | –1 | +1 | –1 | +1 | –1 | –1 | |
| +1 | –1 | +1 | +1 | –1 | –1 | +1 | –1 | |
| +1 | +1 | +1 | –1 | +1 | –1 | –1 | –1 |
