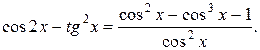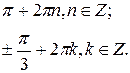Приведение подобных слагаемых
1.1. Анализ преобразования
Рассмотрим уравнение вида 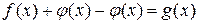 . Его область определения D задают выражения
. Его область определения D задают выражения 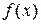 ,
, 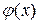 и g(x). Переход к уравнению
и g(x). Переход к уравнению 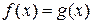 может расширить множество D, так как слагаемое
может расширить множество D, так как слагаемое 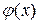 не будет оказывать влияния на область определения полученного уравнения. Следовательно, возможны посторонние корни, которые устраняются проверкой их принадлежности области определения данного уравнения, либо непосредственной подстановкой в него.
не будет оказывать влияния на область определения полученного уравнения. Следовательно, возможны посторонние корни, которые устраняются проверкой их принадлежности области определения данного уравнения, либо непосредственной подстановкой в него.
Таким образом, уравнение 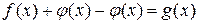 с областью определения D равносильно системе
с областью определения D равносильно системе 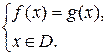
Рассмотрим ряд примеров.
Пример 1. Решить уравнение 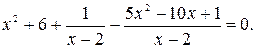
Область определения данного уравнения 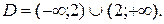 Выполним тождественные преобразования дроби
Выполним тождественные преобразования дроби 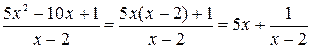 , не меняющие области определения данного уравнения. Получим уравнение
, не меняющие области определения данного уравнения. Получим уравнение 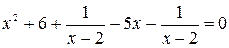 , равносильное данному при
, равносильное данному при 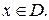 Следующее преобразование (приведение подобных слагаемых) может нарушить равносильность за счёт расширения области определения данного уравнения, поэтому перейдём к системе
Следующее преобразование (приведение подобных слагаемых) может нарушить равносильность за счёт расширения области определения данного уравнения, поэтому перейдём к системе 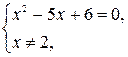 решая которую, найдём корень
решая которую, найдём корень 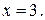
Ответ: 3.
Пример 2. Решить уравнение 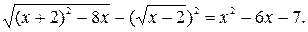
Преобразуя левую часть данного уравнения в области его определения 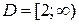 , получим
, получим 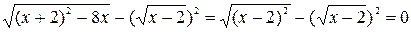 .
.
В результате данное уравнение примет вид 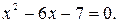 Приведение подобных слагаемых расширило область определения, что может привести к появлению посторонних корней. Следовательно, данное уравнение равносильно системе
Приведение подобных слагаемых расширило область определения, что может привести к появлению посторонних корней. Следовательно, данное уравнение равносильно системе 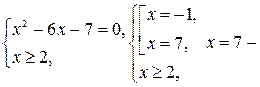 решение системы, а значит и данного уравнения. Ответ: 7.
решение системы, а значит и данного уравнения. Ответ: 7.
Пример 3. Решить уравнение 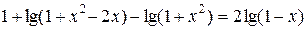 .
.
Область определения данного уравнения 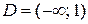 . В результате тождественных преобразований получим уравнение
. В результате тождественных преобразований получим уравнение 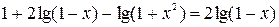 , равносильное данному при
, равносильное данному при 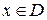 . «Исчезновение» слагаемого
. «Исчезновение» слагаемого 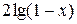 приведёт к уравнению
приведёт к уравнению 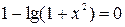 с расширенной по сравнению с D областью определения. Следовательно, данное уравнение равносильно системе
с расширенной по сравнению с D областью определения. Следовательно, данное уравнение равносильно системе 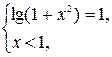 решая которую, получим
решая которую, получим 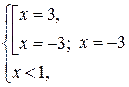 - решение системы.
- решение системы.
Ответ: -3.
Пример 4. Решить уравнение 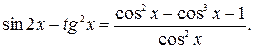
Выполним тождественное преобразование, не меняющие область определения D данного уравнения: разделим дробь 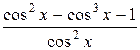 на cos2 x почленно. Получим уравнения
на cos2 x почленно. Получим уравнения 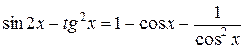 ,
, 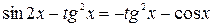 ,
,  равносильные данному на множестве D. Уничтожение одинаковых слагаемых в левой и правой частях последнего уравнения расширит область определения D, что может привести к нарушению равносильности за счёт появления посторонних корней. Следовательно, последнее (и данное) уравнение равносильно системе
равносильные данному на множестве D. Уничтожение одинаковых слагаемых в левой и правой частях последнего уравнения расширит область определения D, что может привести к нарушению равносильности за счёт появления посторонних корней. Следовательно, последнее (и данное) уравнение равносильно системе 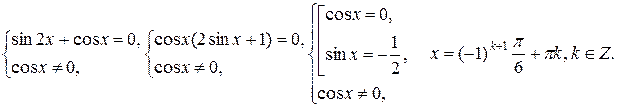 Ответ:
Ответ: 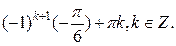
1.2. Комплекс заданий
Решить уравнение устно. Ответы
№1. 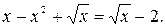 2.
2.
№2. 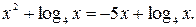 Нет решений.
Нет решений.
№3. 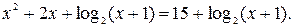 3.
3.
№4. 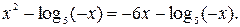 -6.
-6.
№5. 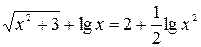 1.
1.
Решить уравнение.
№ 1. 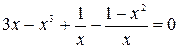 -2; 2.
-2; 2.
№ 2. 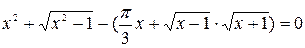 .
. 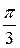 .
.
№ 3. 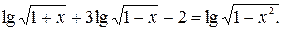 Решений нет.
Решений нет.
№ 4. 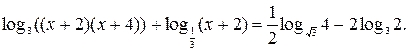 Решений нет.
Решений нет.
№5. .
№6.